шпоргалка. Шпоры_4семестр. 1 Мат методы, модели

• Название: 1 Мат методы, модели
• Анкор: шпоргалка
• Дата: 03.03.2023
• Размер: 0.52 Mb.
• Имя файла: Шпоры_4семестр.doc
• Тип: Закон; #966516
• страница: 5 из 5

45. Необходимые и достаточные условия смешанных оптимальных стратегий в матричной игре с нулевой суммой

Свойство 1. Если чистая стратегия одного из игроков содержится в спектре некоторой его оптимальной стратегии, то выигрыш этого игрока в ситуации, образованной данной чистой стратегией и любой оптимальной стратегией другого игрока, равен значению конечной антагонистической игры.

Свойство 2. Ни одна строго доминируемая чистая стратегия игрока не содержится в спектре его оптимальной стратегии.

Игра G' = (Х',Y',А') называется подыгрой игры G (Х,Y,А), если Х'c Х, U'c U, а матрица А' является подматрицей матрицы А. Матрица А' при этом строится следующим образом. В матрице А остаются строки и столбцы, соответствующие стратегиям Х' и U', а остальные “вычеркиваются”. Всё то что “останется” после этого в матрице А и будет матрицей А'.

Свойство 3. Пусть G = (Х,Y,А) – конечная антагонистическая игра, G' = (Х \ х',Y,А) – подыгра игры G, а х' – чистая стратегия игрока 1 в игре G, доминируемая некоторой стратегией , спектр которой не содержит х'. Тогда всякое решение (хо, yо, u) игры G' является решением игры G.

Свойство 4. Пусть G = (Х,Y,А) – конечная антагонистическая игра, G' = (Х,Y \ y',А) – подыгра игры G, а y' – чистая стратегия игрока 2 в игре G, доминируемая некоторой стратегией , спектр которой не содержит y'.Тогда всякое решение игры G' является решением G.

Свойство 5. Если для чистой стратегии х' игрока 1 выполнены условия свойства 3, а для чистой стратегии y' игрока 2 выполнены условия свойства 4, то всякое решение игры G' = (Х \ х',Y \ y',А) является решением игры G = (Х,Y,А).

Свойство 6. Тройка (хо, yо, u) является решением игры G = (Х,Y,А) тогда и только тогда, когда (хо, yо, кu +а) является решением игры G(Х,Y,кА+а), где  а  – любое вещественное число, к > 0.

Свойство 7. Для того, чтобы  хо = ( ) была оптимальной смешаннойстратегией матричной игры с матрицей А и ценой игры u, необходимо и достаточно выполнение следующих неравенств

         (j = )                       

Аналогично для игрока 2 : чтобы  yо = ( , ..., , ..., ) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:

         (i = )                       

Из последнего свойства вытекает: чтобы установить, является ли предполагаемые (х, y) и u решением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (*) и (**). С другой стороны, найдя неотрицательные решения неравенств (*) и (**) совместно со следующими уравнениями

,                                   

получим решение матричной игры.

Таким образом, решение матричной игры сводится к нахождению неотрицательных параметров решений линейных неравенств (*) (**) и линейных уравнений (***). Однако это требует большого объёма вычислений, которое растёт с увеличением числа чистых стратегий игроков. (Например для матрицы  3 3  имеем систему из 6 неравенств и 2 уравнений). Поэтому в первую очередь следует, по возможности используя свойства 2 и 3, уменьшить число чистых стратегий игроков. Затем следует во всех случаях проверить выполнение неравенства

 = .

Если оно выполняется, то игроки имеют чистые оптимальные стратегии (игрок 1 – чистую максиминная, а игрок 2 – чистую минимаксная). В противном случае хотя бы у одного игрока оптимальные стратегии будут смешанные. Для матричных игр небольшого размера эти решения можно найти, применяя свойства  1 – 5.

47. Нахождение равновесных стратегий в биматричной игре.  Равновесные ситуации.

Ситуация  (i*, j*), в которой выполняются неравенства

  ,     i = 1,2;           ,   j = 1,2,

называется равновесной.

          В равновесной ситуации игроки добиваются наибольших выигрышей стратегиями   i = i*, j = j*. Их называют равновесными стратегиями, а соответствующие элементы  ,   матриц выигрышей – равновесными выигрышами игроков.

        При  B = - A, т.е.

  ,      i, j = 1,2,

биматричная игра превращается в матричную игру. В этом случае из определения равновесных стратегий вытекает

  ,      i, j = 1,2.

Отсюда

,

что означает оптимальность стратегий  i*, j*  в матричной игре (см. п. 5.2) с матрицей выигрыша  А. Следовательно, определение равновесных стратегий включает в себя понятие оптимальных стратегий матричной игры.

        Равновесные выигрыши одновременно максимальны в столбце матрицы  А  и строке матрицы  B  соответственно. Это свойство можно использовать как рабочее правило для нахождения равновесных ситуаций.

         Применим правило к матрицам выигрышей (6.1). Подставив в (6.1) численные значения элементов (6.2), получим

  .

          Ситуация (1,1) равновесная, поскольку для первого столбца матрицы  А  и первой строки матрицы   В  имеем

 2 = а₁₁  ≥  а₂₁ = 1,   0 = b₁₁  ≥  b₁₂ = - 2.

Ситуация (2, 2) тоже равновесная: 0 ≥ - 1  и  -1 ≥ -3. Ситуации (1,2) и (2,1) не равновесные. Равновесные выигрыши игроков (2 и 0) в первой равновесной ситуации превосходят аналогичные выигрыши (0 и –1) во второй, поэтому первая ситуация предпочтительней для игроков. Содержательно в равновесных ситуациях воплощается «закон кармы»: за хорошую подготовку к зачету Студент получает зачет, а за плохую подготовку по справедливости не получает. Моральное удовлетворение Студента и Преподавателя в первой ситуации выше, чем во второй.
48. Смешанные стратегии в биматричной игре. Свойства смешанных стратегий.

Рассмотрим, например, игру «семейный спор» с матрицами выигрыша

  .                                         (6.3)

Ее можно интерпретировать как выбор супругами совместного вечернего развлечения: спортивного соревнования, в котором заинтересован супруг (первый игрок), или балета, которому в равной степени отдает предпочтение супруга (второй игрок). В случае разногласия (выбора разных стратегий) нулевые выигрыши означают безнадежно испорченный вечер.

         Легко видеть, что в игре «семейный спор» нет равновесных ситуаций и, следовательно, нет предпочтительных стратегий, как было в игре о «зачете».

        Построим по аналогии с п. 5.3 смешанное расширение  Г_А,В   этой игры. Определим множества смешанных стратегий

Х = {х= (х₁, х₂):   х₁ + х₂ = 1,  х₁ ≥ 0,    х₂ ≥  0 },

Y = { y = (y₁, y₂):   y₁ + y₂ = 1,  y₁ ≥ 0,    y₂ ≥  0 }

и функции выигрыша

Н₁(х, у) = 2х₁у₁+ х₂у₂,                                       (6.4)

Н₂(х, у) = х₁у₁ + 2х₂у₂.                                       (6.5)

           В модельном представлении в игре  Г_А,В   игроки независимо выбирают смешанные стратегии  х, у  из множеств  Х, Y . Когда выбор стратегий сделан и в игре сложилась  ситуация  (х, у), определяются выигрыши  Н₁(х, у)  и  Н₂(х, у)  первого и второго игрока. Целью каждого игрока является максимизация индивидуального выигрыша путем выбора стратегии из своего множества стратегий.

        Составляющие игры  Г_А,В   имеют такой же содержательный смысл, как в матричной игре:

        х₁ и х₂ – вероятности (частоты) выбора чистых стратегий  i = 1  и  i = 2,

        у₁ и у₂  – вероятности (частоты) выбора чистых стратегий  j = 1  и  j = 2,

        Н₁(х, у) и Н₂(х, у)  – математические ожидания выигрыша («средние» выигрыши) первого и второго игрока в ситуации  (х, у).

        Назовем ситуацию  (х*, у*)  и смешанные стратегии  х*, у*  равновесными, если неравенства

  Н₁(х*, у*) ≥ Н₁(х, у*),     Н₂(х*, у*) ≥ Н₂(х*, у)                  (6.6)

выполняются для любых смешанных стратегий  х, у.

        В равновесной ситуации стратегии   х = х*, у = у*  обеспечивают игрокам максимальные равновесные выигрыши  Н₁(х*, у*), Н₂(х*, у*), поэтому для игроков они представляют первоочередной интерес.

        Покажем существование равновесных ситуаций в смешанных стратегиях. Положим по аналогии с матричной игрой

 х = (х₁, х₂) = (р, 1 - р),   0 ≤ р ≤ 1;

 у = (у₁, у₂) = (q, 1 - q),   0 ≤ q ≤ 3.                              (6.7)

        Формулы (6.7) устанавливают взаимно однозначное соответствие между ситуациями   (х, у)  в смешанных стратегиях и точками  (р, q)  единичного квадрата  0 ≤ р, q ≤  1. Подставляя (6.7) в (6.4), (6.5), получим

  Н₍₁₎ (р, q) = 3рq - р – q + 1,                                         (6.8)

 Н₍₂₎ (р, q) = 3рq – 2р – 2q + 2.                                     (6.9)

          Если  (р*, q*) – прообраз равновесной ситуации  (х*, у*), то по ее определению имеем

  Н₍₁₎ (р*, q*) ≥ Н₍₁₎ (р, q*),       Н₍₂₎ (р*, q*) ≥  Н₍₂₎ (р*, q)                 (6.10)

для любых  0 ≤ р, q ≤ 1   или, учитывая (6.8), (6.9),

 3р*q* - р* - q* + 1 ≥ 3рq* – р – q* + 1,

 3р*q* – 2р* – 2q* + 2 ≥ 3р*q – 2р* – 2q + 2.

Отсюда после несложных преобразований получим систему неравенств

 (р* - р) (q* - 1/3) ≥ 0,   (р* – 2/3) (q* – q) ≥  0

относительно неизвестных   р*, q*, которая должна выполняться для всех  0 ≤ р, q ≤  1. Используя последнее условие, находим три равновесные ситуации  (0, 0), (1, 1), (2/3, 1/3). Определяя по формулам (6.7) их образы и подсчитывая равновесные выигрыши (6.8), (6.9), получим полный набор равновесных ситуаций в игре  Г_А,В   (табл. 6.1).

        В третьей равновесной ситуации игроки имеют равные «средние» выигрыши, что можно расценить как достижение игроками разумного компромисса. Следовательно, отвечающие ей равновесные стратегии и равновесные выигрыши и надо считать решением игры. Суть компромисса между супругами во взаимных уступках с определенной частотой при выборе вечерних развлечений.
49. Многокритериальные задачи. Парето оптимальные стратегии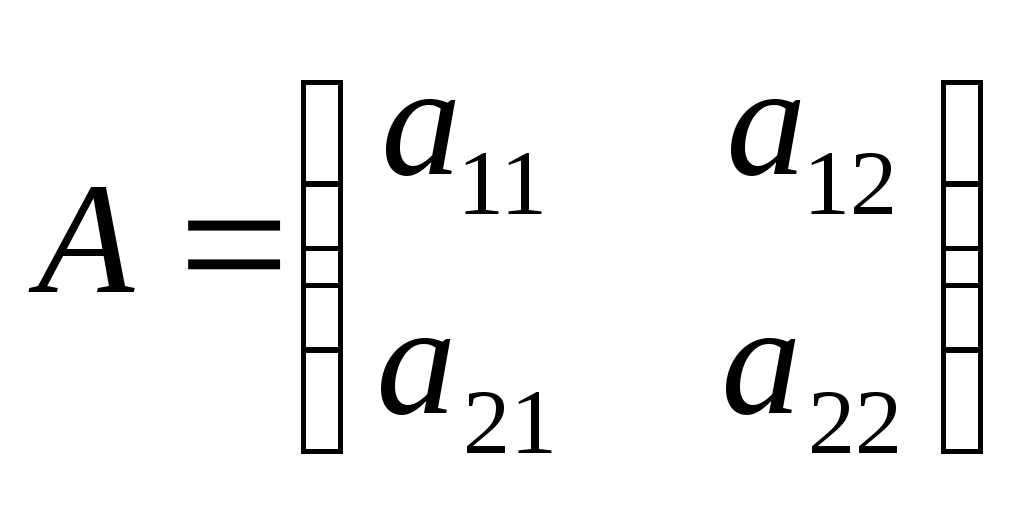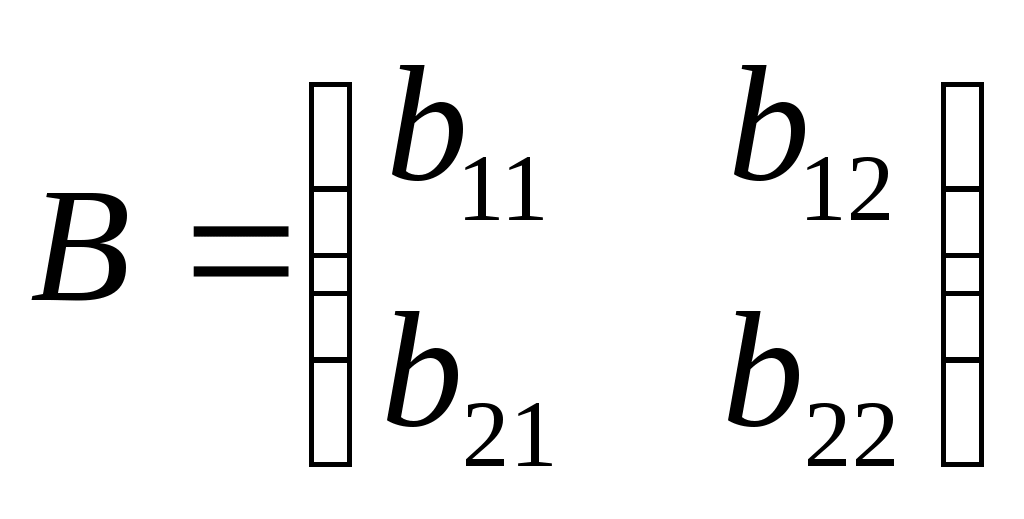



Из ; вытекает, что р = р_*, q = q_*.

Иными словами, в оптимальности по Парето игроки не могут выигрыш для одного увеличить, не уменьшив при этом выигрыш другого.

Оптимальность по Парето:





50. Характерные особенности в задачах игры с природой.

Отличительная особенность игры с природой состоит в том, что в ней имеется 1 активный игрок (игрок 1), а игрок 2 (природа) не дейст­вует сознательно против игрока 1 (по образному выражению А. Эйнштей­на, природа сложна, но не злонамеренна), а выступает как не имеющий конкретной цели партнер по игре, который выбирает свои ходы случайным образом. Термин «природа» характеризует некую объективную действи­тельность. Платежная матрица игры с природой имеет вид:



где aij - выигрыш игрока 1 при выборе им i-й стратегии, а игроком 2 - j-й стратегии (i= 1,2,...,m; j = 1,2,...,n). Следует сразу отметить, что мажори­рование стратегий в игре с природой имеет опред специфику: ис­ключать из рассмотрения можно лишь доминируемые стратегии 1-го игро­ка. Если для всех j = 1,2,...,n выполняется условие aqj < a_kjj, то q-ю страте­гию игрока 1 можно не рассматривать и удалить из матрицы А. Столбцы же, которые отвечают стратегиям игрока 2 (природы) исключать из матри­цы игры А недопустимо, т.к. природа не стремится к выигрышу и для нее нет целенаправленно выигрышных или проигрышных стратегий. С одной стороны отсутствие противодействия упрощает игроку 1 задачу выбора решения, но имеет место проблема обоснования выбора, так как гаранти­рованный результат не известен.

Методы принятия решений в играх с природой зависят от характера неопределенности в поведении игрока 2, т.е. от того, известны или нет ве­роятности состояний (стратегий) природы. В 1 случае мы имеем си­туацию риска, а во 2 - полной неопределенности. В силу этого ино­гда игру с природой задают не в виде матрицы выигрышей, а в виде мат­рицы рисков или матрицы упущенных возможностей



Риском r_ij игрока 1 при использовании им i-й стратегии и при j-м со­стоянии среды (природы) называется разность между выигрышем, кото­рый игрок получил бы, если бы он знал, что наступит j-е состояние среды и выигрышем, который игрок получит, не обладая этой информацией. Зная j-е состояние природы, игрок выбирает ту стратегию, при которой его вы­игрыш максимален, т.е.