шпоргалка. Шпоры_4семестр. 1 Мат методы, модели

• Название: 1 Мат методы, модели
• Анкор: шпоргалка
• Дата: 03.03.2023
• Размер: 0.52 Mb.
• Имя файла: Шпоры_4семестр.doc
• Тип: Закон; #966516
• страница: 3 из 5

27. Целочисленное программирование. Характеристика класса задач, для которых имеет смысл только целочисленное решение. Дополнительное ограничение Гомори.

По смыслу значит части экономич задач, относящихся к задачам лин программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, напр, задачи, в которых переменные означают количество единиц неделимой продукции, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.

Задача лин целочис программирования формулируется следующим образом: найти такое решение (план) Х=(х₁, х₂, …, х_n), при котором линейная функци я

принимает максимальное или минимальное значение при ограничениях , i=1, 2, …, m

, j= 1, 2,…,n. X_j- целые числа.

Для решения задач линейного целочисленного программирования используется ряд методов. Самый простой из них – обычный метод линейного программирования. В случае если компоненты оптимального решения оказываются нецелочисленного, их округляют до ближайших целых чисел. Этот метод применяют тогда, когда отдельная единица совокупности составляет малую часть объема всей совокупности. В противном случае округление может привести к далекому от оптимального целочисленному решению, поэтому используют специально разработанные методы. Методы целочисленной оптимизации можно разделить на 3 основные группы: 1.методы отсечения 2.комбинаторные методы 3.приближенные методы.

Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

• 
  оно должно быть линейным
  
• 
  должно отсекать найденный оптимальный нецелочисленный план
  
• 
  не должно отсекать ни одного целочисленного плана
  

Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением. Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение итп.

Один из алгоритмов решения задачи линейного целочисленно­го программирования (2.4.2)-(2.4.4), предложенный Гомори, основан на симплексном методе и использует достаточно простой способ построения правильного отсечения.

Пусть задача линейного программирования (2.4.1)-(2.4.3) име­ет конечный оптимум и на последнем шаге ее решения сим­плексным методом получены следующие уравнения, выра­жающие основные переменные х₁, х₂, ..., x_j..., x_m через неос­новные переменные x_m+1, x_m+2,…, x_m+i, …, x_n  оптимального решения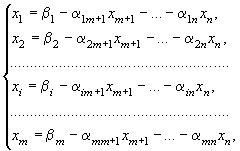

                (2.4.5)

так, что оптимальным решением задачи (2.4.1)-(2.4.3) является Х^* = (β₁, β₂, …, β_i, …β_m,0,0,…,0), в котором, например β­_i - нецелая компонента. В этом случае можно доказать, что неравен­ство

              (2.4.6)

сформированное по i-му уравнению системы (2.4.5), обладает всеми свойствами правильного отсечения.

Для решения задачи целочисленного линейного программиро­вания (2.4.1)-(2.4.4.) методом Гомори используется следующий ал­горитм:

- симплексным методом решается задача (2.4.1)-(2.4.3) без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочис­ленного программирования (2.4.1)-(2.4.4). Если первая задача (2.4.1)-(2.4.3) неразрешима (т.е. не имеет конечного оптимума или условия ее противоречивы), то и вторая задача (2.4.1)-(2.4.4) также неразре­шима;

- если среди компонент оптимального решения есть неце­лые, то выбирается компонента с наибольшей целой частью и по соответствующему уравнению системы (2.4.5) формируется пра­вильное отсечение (2.4.6);

- неравенство (2.4.6) путем введения дополнительной неотрицатель­ной целочисленной переменной преобразовывается в равносильное уравнение

           (2.4.7)

 и включается в систему ограничений (2.4.2);

- полученную расширенную задачу решают симплексным ме­тодом. Если найденный оптимальный план будет целочисленным, то задача целочисленного программирования (2.4.1)-(2.4.4) решена. В противном случае следует вернуться к пункту 2 алгоритма и повторить цикл до тех пор, пока не будет получен оптимальный план .

Если задача разрешима, то оптимальный целочисленный план будет найден после конечного числа шагов (итераций).

Если в процессе решения появится уравнение (выражающее основную переменную через неосновные) с нецелым свободным членом и целыми остальными коэффициентами, то соответст­вующее уравнение не имеет решения в целых числах. В этом слу­чае и данная задача не имеет целочисленного оптимального ре­шения.
28. Транспортная задача линейного программирования. Метод потенциалов.

Цель транспортн задачи- разработка наиболее рациональн путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок.

Транспортная задача ставится так: имеется mпунктов отправления_, в которых сосредоточены запасы каких-то однородных грузов. Имеется n пунктов назначения подавшие заявки соответственно на груза. Известны стоимости р_ij перевозки единицы груза от каждого пункта отправления до каждого пункта назначения. Все числа р_ij, образующие прямоугольную таблицу заданы. Требуется составить такой план перевозок, чтобы все заявки были выполнены, а общая стоимость всех перевозок была минимальна. Далее, предполагается, что



где b_i есть количество продукции, находящееся на складе i, и a_j – потребность потребителя j.

Алгоритм метода потенциалов:

Алгоритм метода потенциалов состоит из предварительного этапа и повторяющегося основного этапа.

Предварительный этап.

Каким-либо способом ищется допустимый план Х методом северо-западного угла или минимального элемента).

Для полученного плана строится система m+n чисел , , таких, что ,   .

Построенная система Ui и Vj исследуется на потенциальность, то есть, план X исследуется на оптимальность. Для этого проверяется , .

    Если система не потенциальна, то переходят к основному этапу (т.к. план не оптим), иначе оптим план найден.

Основной этап.

Улучшаем план, то есть от плана X переходим к плану X’ такому, что .

Для плана X’ строим новую систему , , , такую, что ,   .

Исследуем систему на потенциальность. Если система не потенциальна, то переходим на п.1. Иначе найден оптим план.

Допустимый опорный план транспортной задачи называется невырожденным, если число заполненных клеток транспортной таблицы, т.е. число положительных перевозок , равно m + n - 1, где  m – число пунктов отправления, n – число пунктов назначения.

Распределительные   задачи связаны с распределением ресурсов по работам, которые необходимо выполнить. Задачи этого класса возникают тогда, когда имеющихся в наличии ресурсов не хватает для выполнения каждой работы наиболее эффективн образом. Поэтому целью решения задачи, является отыскания такого распред ресурсов по работам, при котором либо минимизир общие затраты, связанные с вып работ, либо максимизир получаемый в результате общий доход.

29. Выбор наиболее эффективного пути улучшения плана при решении закрытой транспортной задачи методом потенциалов. Правила построения цепочек перемещения. Экономическое содержание перемещений. Характеристика задач, решаемых этим методом.

Для решения транспортной задачи методом потенциалов строится система потенциалов ,   . Если опорное решение невырожденно, то число неизвестных на 1 больше числа уравнений. При вырожденном опорном решении число этих уравнений еще меньше. По аналогии симплекс-методом, в невырожденном решении Xij > 0 представляют собой базисные переменные, а Xij = 0 – небазисные. Если опорное решение вырожденно, то часть базисных переменных принимает нулевые значения.

     Пусть первое опорное решение, найденное методом северо-западного угла или методом минимального элемента, является вырожденным. Тогда, чтобы решать задачу методом потенциалов необходимо выбрать в качестве базисных переменных некоторые перевозки Xij =0 и для них также составить уравнения по условию (2) теоремы. Какие перевозки вида Xij = 0 включать в базисные? Выбираются такие клетки таблицы с Xij = 0, чтобы из базисных переменных нельзя было организовать ни одного цикла!

     При переходе к новому улучшенному плану задачи в небазисные переменные переводится перевозка из отрицательной полуцепи, которая находится nfr: . В вырожденной задаче это значение может достигаться на нескольких перевозках Xij отриц полуцепи. В этом случае на каждом шаге в небазисные переменные переводится та мин перевозка отриц полуцепи, которая связана с пунктом производства, имеющим меньший номер. Это правило уменьшает вероятность возникновения зацикливания, что само по себе достаточно редкое явление в практических задачах.
30. Матрица (математическая модель) открытой транспортной задачи. Условный потребитель (получатель). Характеристика задач, решаемых этим методом.

При открытой транспортной задаче сумма запасов не совпадает с суммой потребностей, т е .

При этом

1)Если , то объем запасов превышает объем потребления.

Для решения вводят фиктивного (n+1)-го потребителя.

Модель такой задачи имеет вид

2)Если ,то объем потребления превышает объем запасов.

Для решения вводят фиктивного (m+1)-го поставщика.

Модель:

Открытая модель решается приведением к закрытой модели.

В случае (а), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель B_n+1, потребности которого b_n+1 = . В случае (б), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик A_m+1, запасы которого a_m+1 = .

Стоимость перевозки единицы груза как фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.
31. Вырождение плана и его преодоление при решении транспортной методом потенциалов

33. Признаки оптимальности плана транспортной задачи при решении методом потенциалов

Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке совершает поворот на 90 , Знаком " + " отмечают те вершины, в которых перевозки увеличиваются, а знаком "- " - те вершины, в которых перевозки уменьшаются. Перемещение какого-то кол-ва единиц груза по циклу означает увеличение перевозок на это кол-о единиц в положит вершинах и уменьшение перевозок на это же количество единиц в отрицат вершинах. При этом, если перевозки остаются неотрицат, план остается допустимым. Стоимость плана при этом может меняться.

Ценой цикла называется увеличение стоимости перевозок при перемещении единицы груза по этому циклу. Очевидно, цена цикла равна алгебраической сумме стоимостей, стоящих в вершинах цикла, при этом стоимости в положит вершинах берутся со знаком " +", а стоимости в отрицат вершинах берутся со знаком " - ".

Идея метода потенциалов состоит в следующем. Для любой свободной клетки транспортной таблицы всегда существует единственный цикл, положит вершина которого лежит в этой свободной клетке, а все остальные - в базисных. Если цена такого цикла отрицат, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицат вершинах цикла (если переместить большее число единиц груза, возникнут отриц перевозки). Если циклов с отриц ценой нет, то это означает, что дальнейшее улучшение плана невозможно, т.е. оптимальный план найден.

Для нахождения циклов с отрицательной ценой вводится система платежей (альфа)i , i = 1,m; βj, j = 1,n и определяются величины Ćij (cо штрихом) = (альфа)i + βj, называемые "псевдостоимостями" перевозок единицы груза из пункта i в пункт j. При этом цена цикла пересчета для каждой свободной клетки равна Cij – Cij (со штрихом), если платежи определять из условий (альфа)i + βj = Cij для всех базисных клеток (i, j).
32. Этапы решения транспортной задачи методом потенциалов

Шаг 1. Строим опорный план (методом северо-западного угла) с n + m - 1 базисными клетками.

Шаг 2. Определяем платежи (альфа)i , i = 1,m; βj, j = 1,n из условий (альфа)i + βj = Cij для всех базисных клеток. Один из платежей (например a1 ) полагаем равньм нулю.

Шаг 3. Считаем псевдостоимости Ćij (cо штрихом) = (альфа)i + βj для всех свободных клеток. Если Cij ≥ Cij (со штрихом) для всех клеток, то план оптимален. Вычисляем значение целевой функции L на этом плане и исследования прекращаем. Шаг 4. Если есть свободная клетка, для которой Cij < Cij (со штрихом), то улучшаем план, перебрасывая перевозки по циклу этой свободной клетки.

Шаг 5. Возвращаемся к шагу 2 для пересчета платежей нового опорного плана.
34. Расчет опорного (базисного) плана транспортной задачи методом «северо-западного угла».

Дадим переменной _х11 максимально возможное значение или, иными словами, максимально возможную поставку в клетку (1,1) — "северо-западный" угол таблицы поставок: х₁₁ = min {60, 20} = 20. После этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего 1 столбец табли­цы поставок выпадет из последующего рассмотрения (заполнен­ные клетки будем перечеркивать сплошной линией (см. табл. 7.2) клетки, выпавшие из последующего рассмотрения, перечеркнуты пунктирной линией. В таблице поставок найдем новый "северо западный" угол — клетку (1,2) и дадим в нее максимально воз­можное значение. Учитывая, что 1-й поставщик уже отдал 20 единиц груза и у него осталось только 40 = 60—20 единиц груза, получаем, что х₁₂ = min {40, 110} = 40. После этого мощность 1-го поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы поставок (перечеркиваем сплошной лини­ей клетку (1,2) и пунктирной линией оставшиеся свободные клет­ки 1 строки). В оставшейся таблице снова находим "северо западный угол" и т. д. В результате получаем следующее исходное распределение поставок (см. табл.7.2).



Число заполненных клеток в полученном распределении оказалось равным m+n— -1 = 3+4-1 =6, т.е. числу основных (ба­зисных) переменных. Это, конечно, не слу­чайно. Действитель­но, на каждом шаге (кроме последнего) данного метода из рассмотрения выпадали либо строка, либо столбец, а на послед­нем шаге и столбец, и строка. Поэтому число заполненных кле­ток (число шагов) на единицу меньше, чем сумма числа строк и столбцов таблицы поставок, т.е. равно т+п—1. Оказывается (см. теорему 7.2), что эта особенность шагов метода "северо­ западного" угла служит причиной того, что полученное рас­пределение является базисным.

Существенный недостаток метода "северо-западного" угла состо­ит в том, что он построен без учета значений коэффициентов затрат задачи