шпоргалка. Шпоры_4семестр. 1 Мат методы, модели

• Название: 1 Мат методы, модели
• Анкор: шпоргалка
• Дата: 03.03.2023
• Размер: 0.52 Mb.
• Имя файла: Шпоры_4семестр.doc
• Тип: Закон; #966516
• страница: 4 из 5

35. Расчет опорного (базисного) плана транспортной задачи методом минимальных тарифов.

Находим в таблице поставок (см. табл.) клетки с наи­меньшим коэффи­циентом затрат.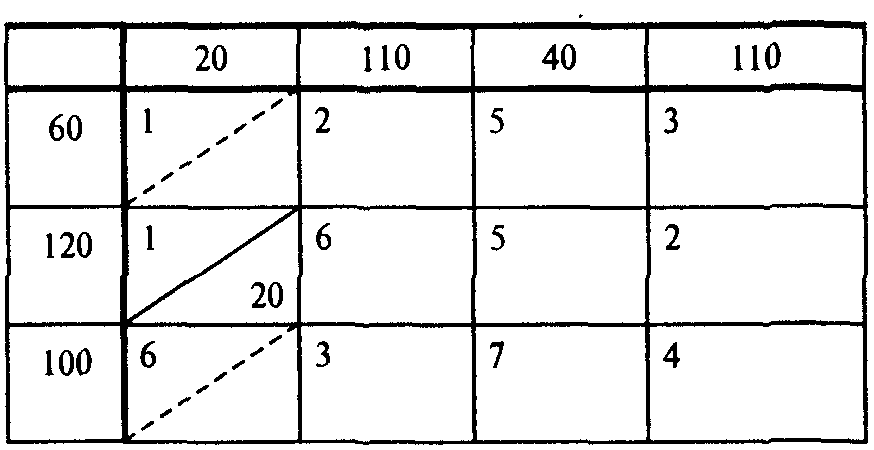



Та­ких клеток две — (1,1) и (2,1) с коэф­фициентами затрат, равными 1. Срав­ним максимально возможные поставки для этих клеток: для клетки (1,1) х₁₁ = = min {60, 20} = 20, для клетки (2,1) х₂₁= min {120, 20} = = 20. Так как они совпадают, то мак­симально возмож­ную поставку даем в любую из них. Напр, даем постав­ку, равную 20 едини­цам, в клетку (2,1). В результате спрос пер­вого потребителя удо­влетворен и первый столбец таблицы по­ставок выпадает из последующего рас­смотрения (табл. 7.3).

В оставшейся таблице наименьшим коэффициентом затрат об­ладают две клетки: с₁₂ = С₂₄= 2. Сравним макс возможные поставки для этих клеток: для клетки (1,2) х₁₂ = min {60, 110} = 60; для клетки (2,4) х₂₄ ⁼ min {120-20, 110} = 100. Даем поставку в клетку (2,4), для которой макс возможная поставка ока­залась больше: x24 ⁼ 100. При этом из рассмотрения выпадает 2 строка таблицы поставок (табл. 7.4).



Аналогично, продолжая заполнение таблицы поставок шаг за шагом, получаем x₁₂ = min{60, 110} = 60, Х₃₂ = min{100, 110-60} = 50, х₃₄ = min {100-50, 110-100} = 10, х₃₃ = min {100-60, 40} = 40 (табл. 7.5)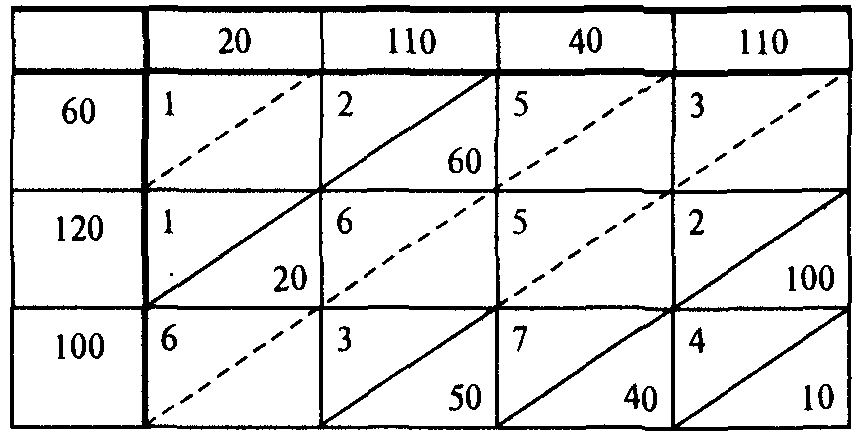



Сравним найденное распределение поставок с распределением, полученным для той же задачи по методу "сев-западн" угла (см. задачу 7.2, табл. 7.2). Вычислим для каждого из этих распре­делений суммарные затраты в денежных единицах: F₀ = 1 * 20 + 2 * 40 + 6* 70 + 5 * 40 + 2 * 10 + 4 * 100 = 1140 ; в задаче 7.3: F₀ = 1 * 20 + 2 * 60 + 3 * 50 + 2 * 100 + 7 * 40 + 4 *10 = 810.
36. Характеристика задачи о назначениях. Методы нахождения оптимального решения.

Частным случаем транспортной задачи является задача о назначениях, в которой число пунктов производства равно числу пунктов назначения, т.е. транспортная таблица имеет форму квадрата. Кроме того, в каждом пункте назначения объем потребности равен 1, и величина предложения каждого пункта производства равна 1. Любая задача о назначениях может быть решена с использованием методов линейного программирования или алгоритма решения транспортной задачи.

Данная задача решается с помощью алгоритма, носящего название "Венгерского метода", состоящего из 3 этапов:

1 этап:

1 Формализация проблемы в виде транспортной таблицы

2 В каждой строке таблицы найти наименьший элемент и вычесть его из всех элементов данной строки

3 Повторить ту же процедуру для столбцов

Задачей является распределение всех подлежащих назначению единиц в клетки с нулевой стоимостью. Оптимальное значение целевой функции в этом случае равно нулю.

2 этап:

1 Найти строку, содержащую только одно нулевое значение, в его клетку помещается один элемент (0 обводится квадратиком). Если такие строки отсутствуют, допустимо начать с любой строки.

2 Зачеркнуть оставшиеся нулевые значения данного столбца

3 Повторять пп.1-2, пока продолжение указанной процедуры окажется невозможным

Если окажется, что имеется несколько нулей, которым не соответствуют назначения, и которые остались незачеркнутыми, необходимо:

4 Найти столбец, содержащий только одно нулевое значение, в его клетку помещается один элемент.

5 Зачеркнуть оставшиеся нули в данной строке

6 Повторять пп.4-5, пока продолжение указанной процедуры окажется невозможным

Если выяснится, что таблица содержит неучтенные нули - повторить пп. 1-6

Если решение является допустимым, оно оптимально. Если нет - перейти к этапу 3.

3 этап: (Если решение является недопустимым)

1 Провести минимальное количество прямых через столбцы и строки матрицы таким образом, чтобы они проходили через все нули, содержащиеся в таблице

2 Найти наименьший из элементов, через которые не проходит ни одна прямая

3 Вычесть его из всех элементов, через которые не проходят прямые

4 Прибавить его ко всем элементам, лежащим на пересечении прямых

5 Элементы, через которые проходит только одна прямая, оставить неизменными

В результате в таблице появится как минимум одно новое нулевое значение. Вернуться к этапу 2 и повторить решение заново.
37. Формулы расчёта потенциалов занятых клеток и расчёта оценок свободных

Ui + Vj = Cij (для занятых клеток)

∆ij = Ui + Vj – Cij (для свободных клеток).
39. Характеристика условий и правил игры двух лиц с нулевой суммой.

Математическая модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте, — игроками, а исход конфликта — выигрышем. Для каждой формализованной игры вводятся правила, т.е. система условий, определяющая: 1) варианты действий игро­ков; 2) объем информации каждого игрока о поведении партне­ров; 3) выигрыш, к которому приводит каждая совокупность дей­ствий. Как правило, выигрыш (или проигрыш) может быть задан количественно; например, можно оценить проигрыш нулем, вы­игрыш — единицей, а ничью — 1/2.

Игра называется игрой с нулевой суммой, или антагонистиче­ской, если выигрыш одного из игроков равен проигрышу другого, т.е. для полного задания игры достаточно указать величину одно­го из них. Если обозначить а — выигрыш одного из игроков, Ь — выигрыш другого, то для игры с нулевой суммой в = —а, поэтому достаточно рассматривать, например а.
40. Максиминные и минимаксные стратегии игры конкурентов.

Ai Bj	B1	B2	…	Bn
A1	а11	a12	…	a1n
A2	а21	a22	…	a2n
…			…	…
Am	аm1	am2	..	amn

Среди всех чисел а_i (i = 1, 2, ..., т) выберем наибольшее: а = mах а,. Назовем а нижней ценой игры, или максимальным

выигрышем (максимином). Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно,

а = mах min a_ij.

Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А; выбирая стратегию В_j, он учитывает макси­мально возможный при этом выигрыш для А. Обозначим

b_; = mах а_ij

Среди всех чисел b_j выберем наименьшее b = min b_j и назовем b верхней ценой игры или минимаксным выигрышем (минимаксом). Это гарантированный проигрыш игрока В. Следовательно,

b= min mах a_ij.

Стратегия, соответствующая минимаксу, называется минимакс­ной стратегией.

Принцип, диктующий игрокам выбор наиболее "осторожных" минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника.
41. Хаар-ка максиминной и минимаксной стратегии игры 2 лиц с нулевой суммой

42.Важнейшие свойства максиминных (минимаксных) стратегий игровых матриц с «седловой точкой» (точкой равновесия)

Если верхняя и нижняя цены игры совпадают, то общее значе­ние верхней и нижней цены игры а = b = V называется чистой ценой игры, или ценой игры. Минимакс­ные стратегии, соответствующие цене игры, являются оптимальны­ми стратегиями, а их совокупность — оптимальным решением, или решением игры. В этом случае игрок А получает максимальный га­рантированный (не зависящий от поведения игрока В) выигрыш V, а игрок В добивается минимального гарантированного (вне зависи­мости от поведения игрока А) проигрыша V. Говорят, что решение игры обладает устойчивостью, т.е. если один из игроков придержи­вается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Пара чистых стратегий A_i и B_j дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент а_ijявляется одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация, если она существует, называется седловой точкой (по аналогии с поверхностью седла, которая ис­кривляется вверх в одном направлении и вниз — в другом).

43. Смешанные стратегии теории игр. Свойства смешанных стратегий.

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В таком случае можно полу­чить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_a игрока А называется применение чистых стратегий A₁, А₂, ..., A_i .... A_m с вероятностями р₁, Р₂,..., p_i

.... р_т, причем сумма вероятностей равна 1. Смешанные стратегии игрока А записываются в виде матрицы



или в виде строки 5_А =(Р₁,Р₂,...Р_i,...,р_m)- Аналогично смешан­ные стратегии игрока В обозначаются:

где сумма вероятностей появления стратегий равна 1

Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой 1 соответствует чистой стратегии. На основании принципа минимакса определяется оптимальное решение игры.

Пусть игра задана платежной матрицей

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию

, а Игрок В — чистую стратегию B₂ (это соответствует 1-му столбцу платежной матрицы Р), равен цене игры v:



Тот же средний выигрыш получает игрок А, если 2-й игрок применяет стратегию В₂, т.е Учитывая, что р₁ + р₂ - 1, получаем систему уравнений для определения опти­мальной стратегии S_a и цены игры V:

Решая эту систему получаем оптимальную стратегию

И цену игры

Применяя теорему об активных стратегиях при отыскании S_в — оптимальной стратегии игрока В, получаем, что при любой чистой стратегии игрока А (А₁или А₂) средний проигрыш игрока В равен цене игры V, т.е.

Тогда оптимальная стратегия определяется формулами:



46. Биматричные игры. Максиминные и минимаксные стратегии игры игроков

                                     (6.1)

с элементами

a₁₁ = 2,       a₁₂ = -1,     a₂₁ = 1,       a₂₂ = 0;                            (6.2)

b₁₁ = 0,       b₁₂ = -2,     b₂₁ = -3,     b₂₂ = 1.

           Как и в матричной игре, пара матриц (6.1) однозначно задает правила биматричной игры. Стратегиями первого и второго игроков служат соответственно номера   i = 1, 2  строк и   j = 1, 2  столбцов этих матриц. Если игроки независимо выбрали свои стратегии  i, j  и в игре сложилась ситуация  (i, j), то выигрышем первого игрока будет элемент  а_{i j}  матрицы  A, а выигрышем второго – элемент  b_{i j}  матрицы  B. Цель каждого игрока состоит в максимизации индивидуального выигрыша.
44. Приведение матричной антагонистической игры к задаче линейного программирования

Играm х п в общем случае не имеет наглядной геометрич интерпретации. Ее решение достаточно трудоемко при больших m*n, однако принципиальных трудностей не имеет, посколь­ку может быть сведено к решению задачи линейного программи­рования. Покажем это. Пусть игра т х п задана платежной мат­рицей р =(a_ij), i =1, 2, т;j= 1,2, п. Игрок А обладает стра­тегиями А₁ А₂, А_т игрок В — стратегиями В₁, В₂, В_п. Необ­ходимо определить оптимальные стратегии S*_A= (Р₁,Р₂,,,,Р_m) иS*_B (q₁, q₂, q_n) гдеp*,q* — вероятности применения соот­ветствующих чистых стратегийA_i В_j

Р₁+Р₂+Р_m=1 q₁+ q₂+ q_n=1

Оптим стратегияS*_A удовлетворяет след требо­ванию Она обеспечивает игроку А средний выигрыш, не мень­шим, чем цена игры v, при любой стратегии игрока В и выиг­рыш, равный цене игры v, при оптим стратегии игрока В. Без ограничения общности полагаем v> 0; этого можно добиться, сделав все элементыa_ij > 0. Если игрок А применяет смешанную стратегиюS*_A= (Р₁,Р₂,,,,Р_m) против любой чистой стратегии Bjигрока B то он получает средний выигрыш, или математическое ожидание выигрыша aj= a_1jp₁ +a_2jP₂+a_mjP_mj=1,2,..n(т.е. элементы j-го столбца платежной матрицы почленно умножаются на соотв вероятности стратегий А₁,A₂…A_m и резуль­таты складываются).

Для оптим стратегии S*_A все средние выигрыши не меньше цены игры v, поэтому получаем систему неравенств:


Каждое из неравенств можно разделить на число v > 0. Введем новые переменные:

X₁=p₁/v Тогда система примет вид:(9.13)



Цель игрока А — максимизировать свой гарантированный вы­игрыш, т.е, цену игры v.

Разделив на v ≠ 0 равенство Р₁+Р₂+Р_m=1получаем, что переменные x_i,(i=1,2,…m) удовлетворяют условию: Х₁+Х₂ +… +х_m = 1/v. Максимизация цены игры v эквивалентна мини­мизации величины 1/v, поэтому задача может быть сформулиро­вана следующим образом: определить значения переменных x_i ≥ 0, i= 1, 2, т, так, чтобы они удовлетворяли лин ограничени­ям (9.13) и при этом лин функция

Z=x₁ + х₂+...+х_m (9.14)

обращалась в минимум. Это задача лин программирования. Решая задачу (9.13)—(9.14), получаем оптим решение Р₁ P₂….Р_m ^и оптим стратегию S*_A.

Для определения оптим стратегии S*_A - (q₁,q₂….q_n) следует учесть, что игрок В стремится минимизировать гаранти­рованный выигрыш, т.е. найти mах 1/v. Переменные q₁,q₂….q_n удовлетворяют неравенствам:



которые следуют из того, что средний проигрыш игрока В не пре­восходит цены игры, какую бы чистую стратегию не применял игрок А.

Если обозначить y_j=q_j/v j=1,2,3….n.(9.16) то получим систему неравенств(9.17):


Переменные у_i(j =1, 2,..., n) удовлетворяют условию У1 + У₂+.-.+У_n= 1/v.

Игра свелась к следующей задаче.

Определить значения переменных у_j≥ 0, j = 1, 2, ..., п, которые

удовлетворяют системе неравенств (9.17) и максимизируют линей­ную функцию

Z' = y₁+y₂+…y_n

Решение задачи линейного программирования (9.16), (9.17) определяет оптимальную стратегию S*_в= (q₁,q₂….q_n ).При этом цена игры

v=1/mахZ' = 1/minZ.