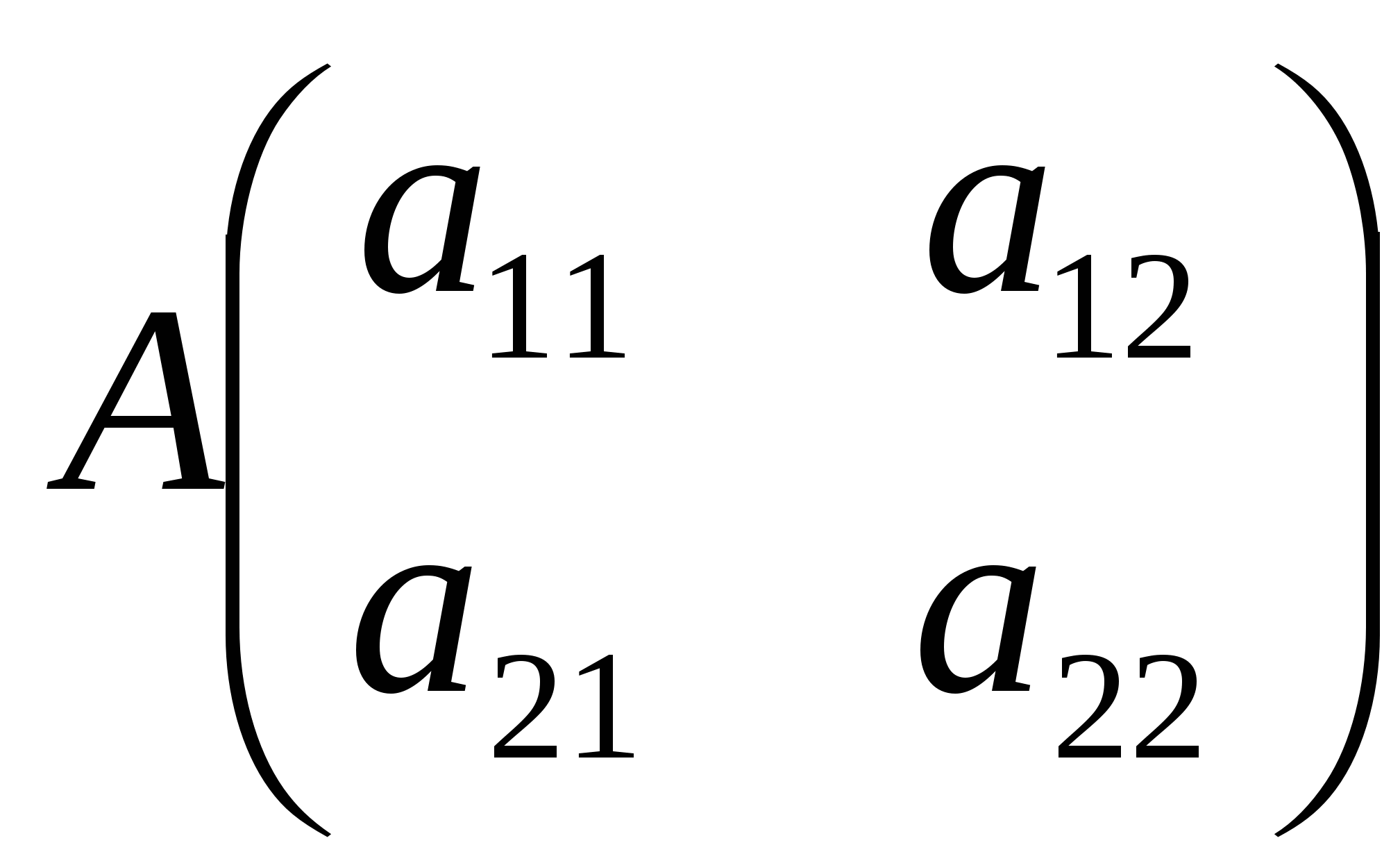1. Матрицы. Линейные операции над ними и их свойства
 Скачать 0.98 Mb.
|
|
1. Матрицы. Линейные операции над ними и их свойства. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.  Матрицы равны между собой, если равны все их соответствующие элементы. Матрица, у которой число строк и столбцов равно – называется квадратной. Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной. Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е. Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной. Матрица, у которой все элементы равны нулю, называется нулевой.         Умножение матриц. Транспонирование. Свойства.Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.  где       Матрица, полученная заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной, к данной. Вопрос 2. Определители. Свойства определителей. Определители матриц. Свойства определителей. Миноры и алгебраические дополнения. 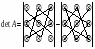 Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали. Свойства:
Вопрос 5. Скалярное произведение двух векторов и его основные свойства. Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.   Вопрос 6. Векторное произведение векторов и его свойства. Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую. Векторным произведением вектора  на вектор  называется вектор  , который:
 , где 
Свойства: 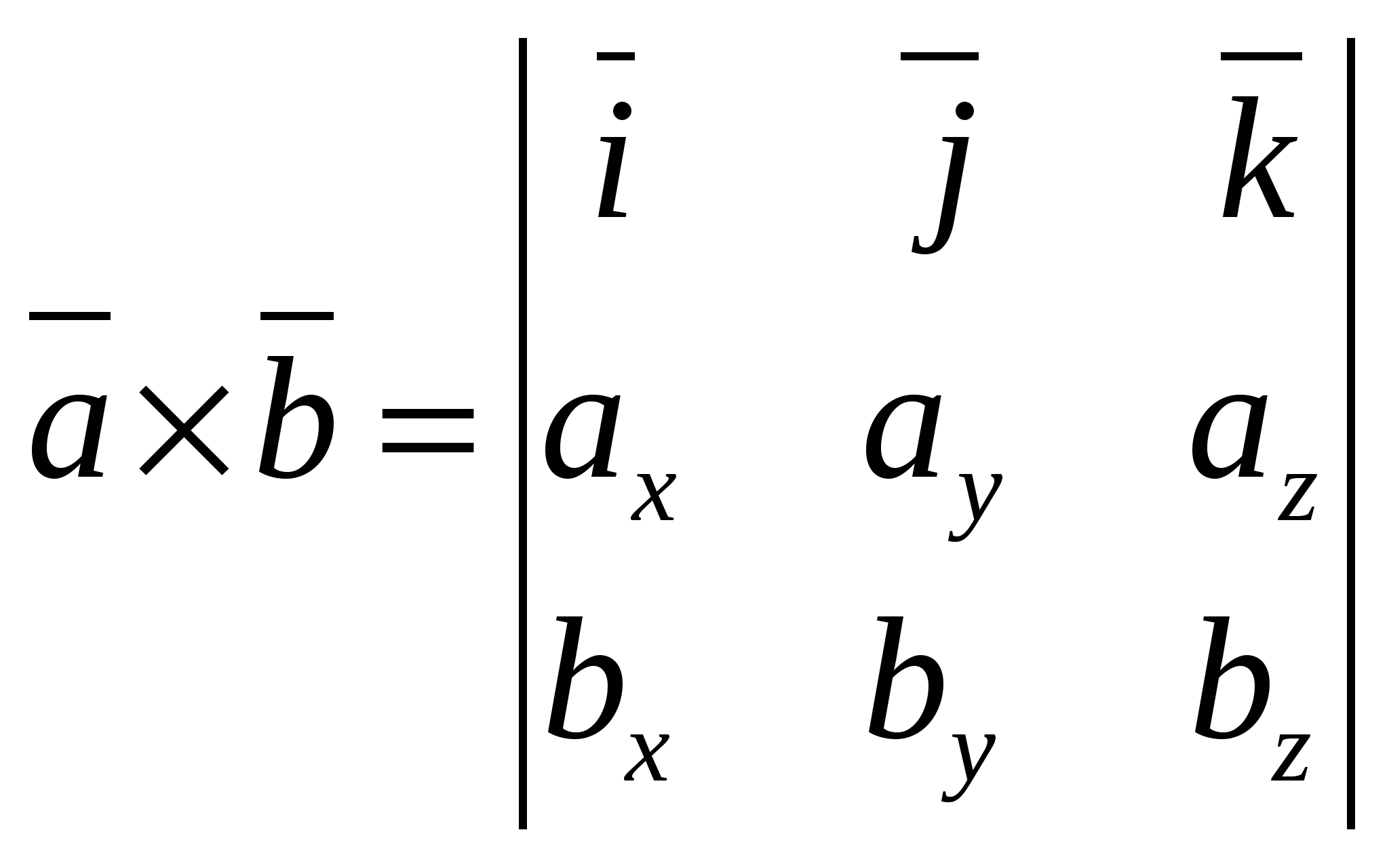     Вопрос 16. Уравнение окружности эллипса, гиперболы, параболы. Эллипс. Определение. Вывод канонического уравнения.Эллипсом называется геометрическое место всех точек плоскости, сумма расстояний от которых до фокусов есть величина постоянная, большая, чем расстояние между фокусами. Пусть М (х;у) – произвольная точка эллипса. Т.к. MF1 + MF2 = 2a 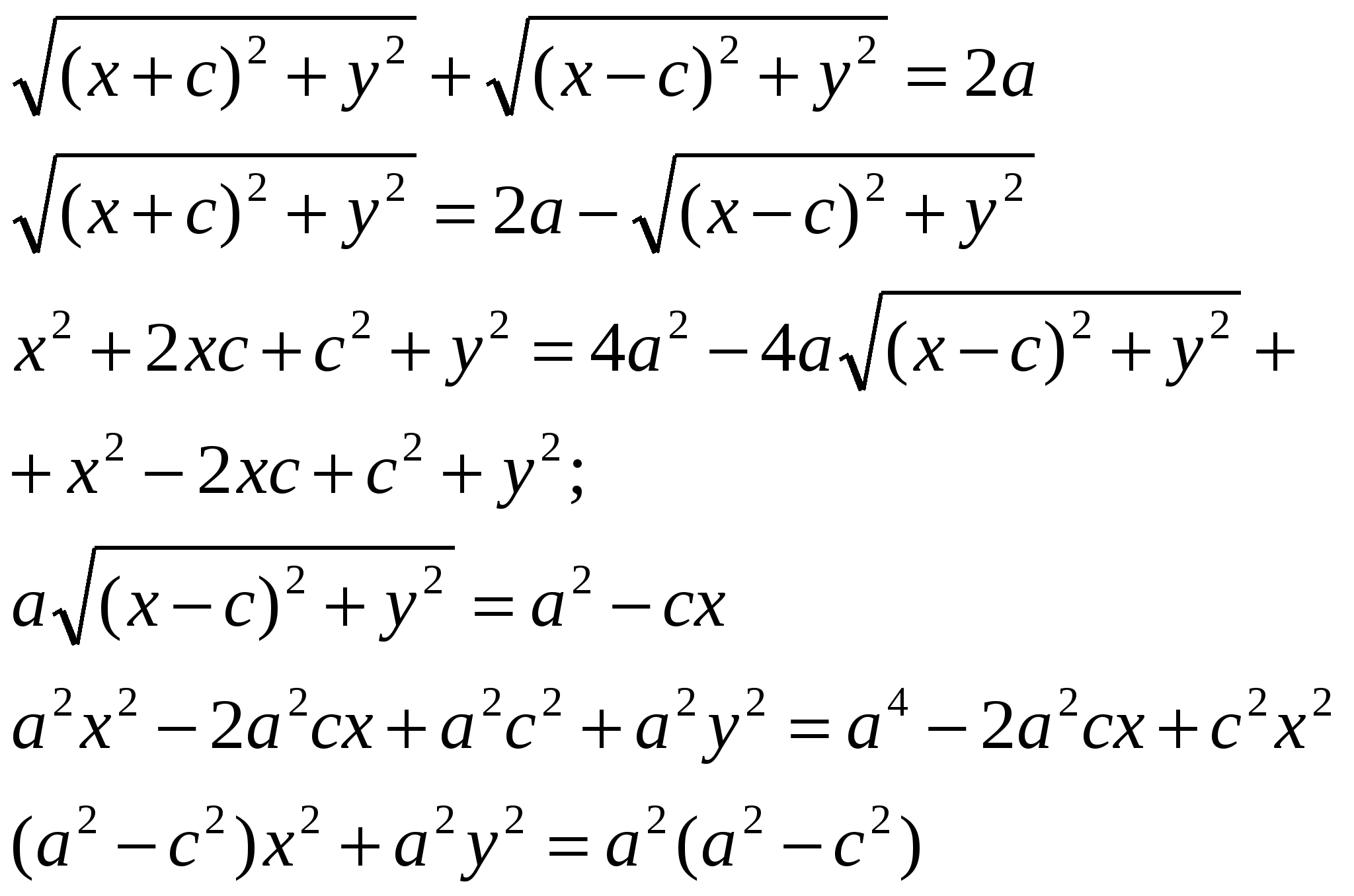 Т.к.  То получаем  Или  Гипербола. Определение. Вывод канонического уравнения.Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная. Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1 – MF2|=2a или MF1 – MF2=±2a, 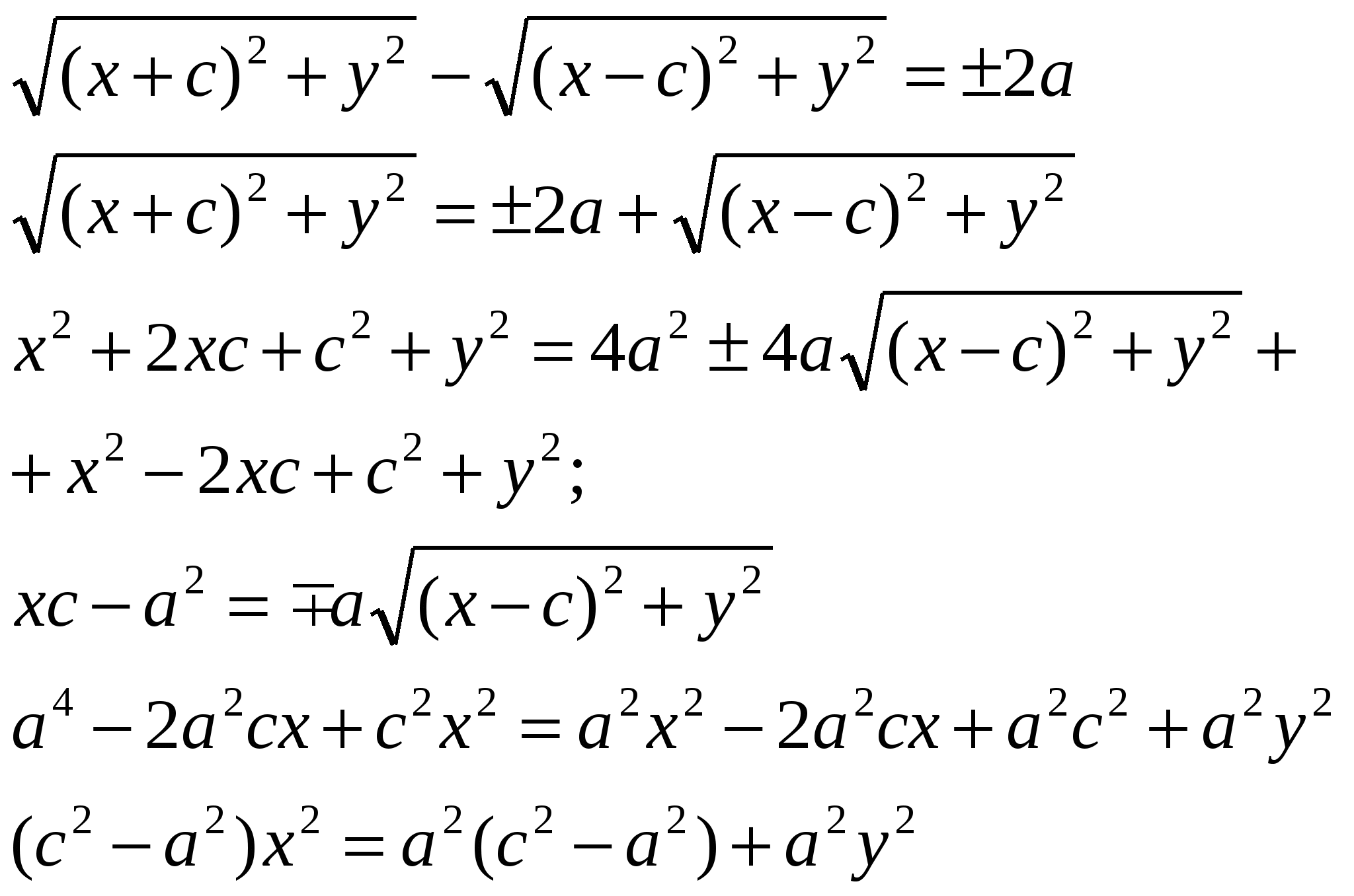   Парабола. Определение. Вывод канонического уравнения.Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0. Пусть M(x;y) – произвольная точка M с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению MF=MN. 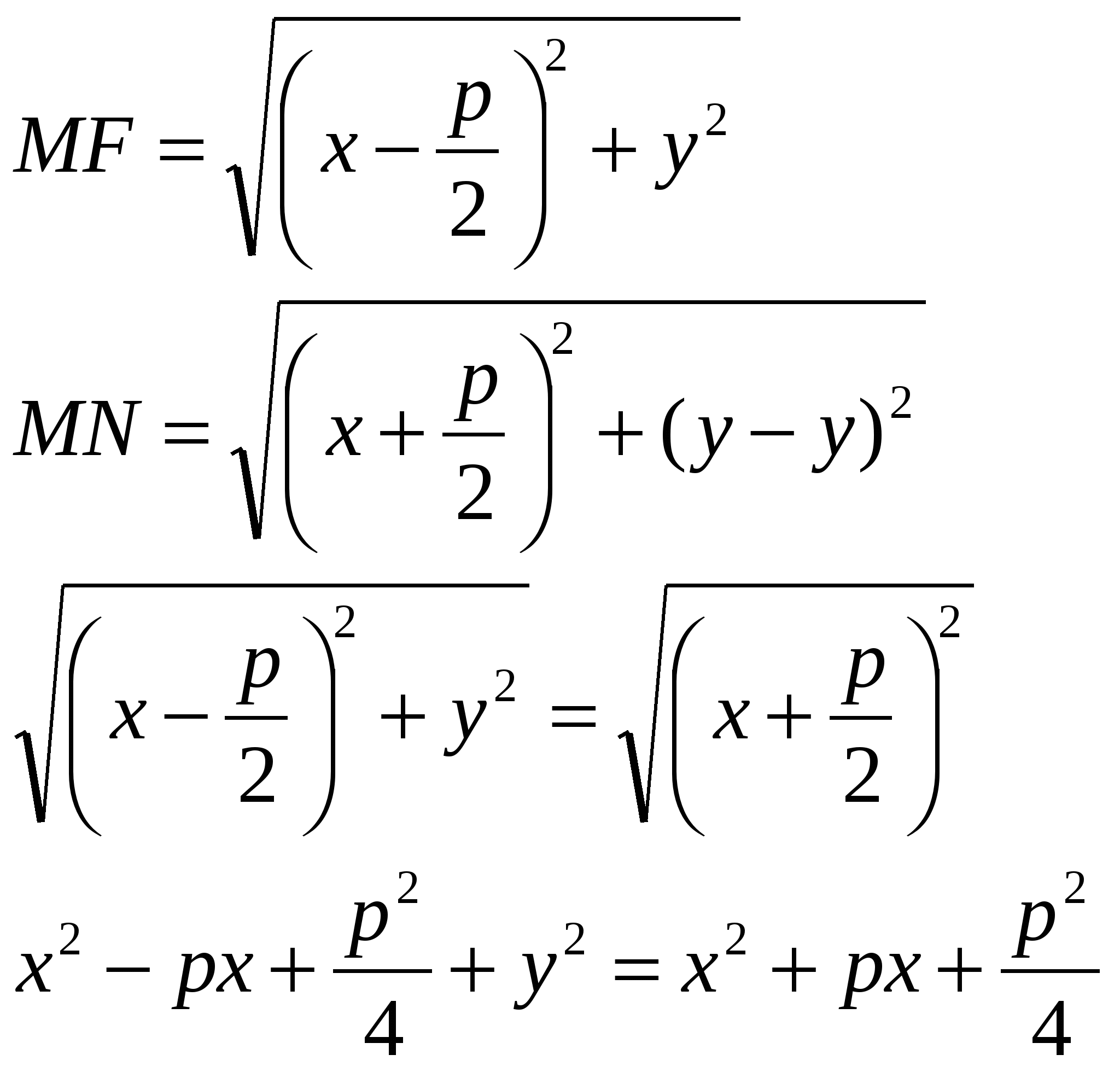  Вопрос20. 1й и 2й замечательные пределы. 1 замечательный предел.  Возьмем круг радиуса 1, обозначим радианную меру угла MOB через Х. Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда 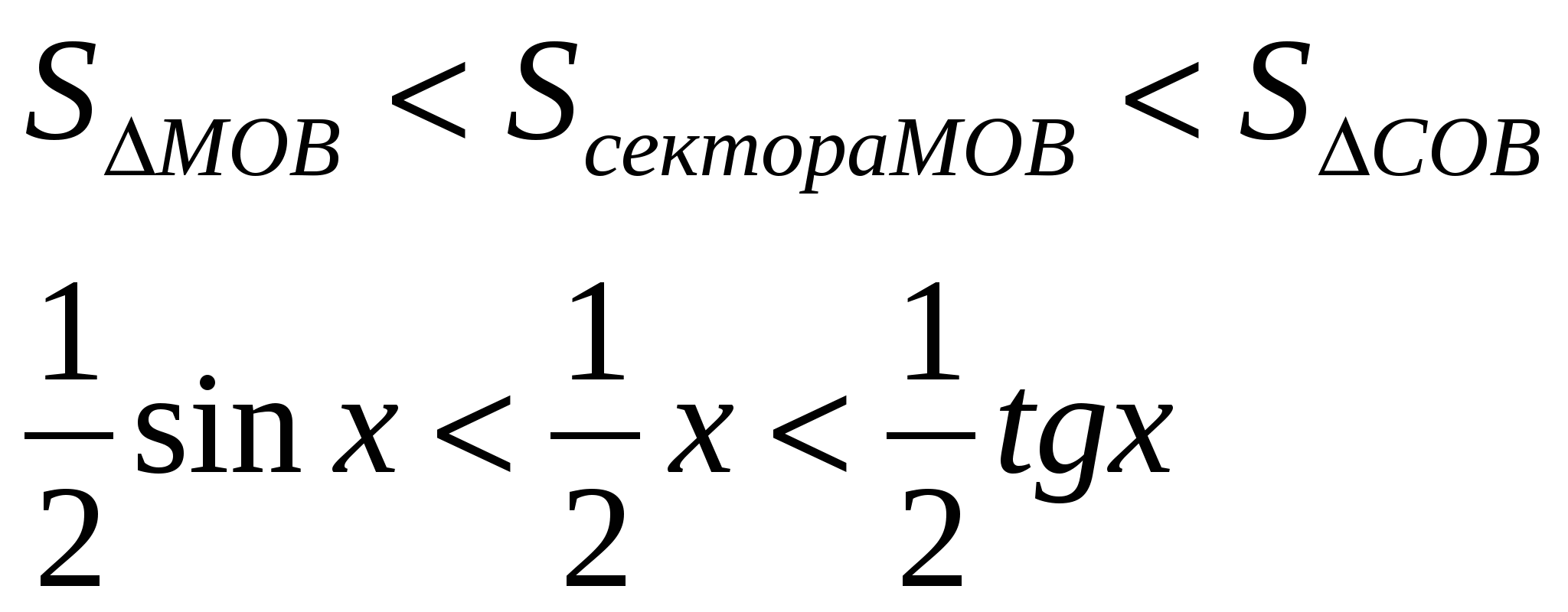 Разделим все на 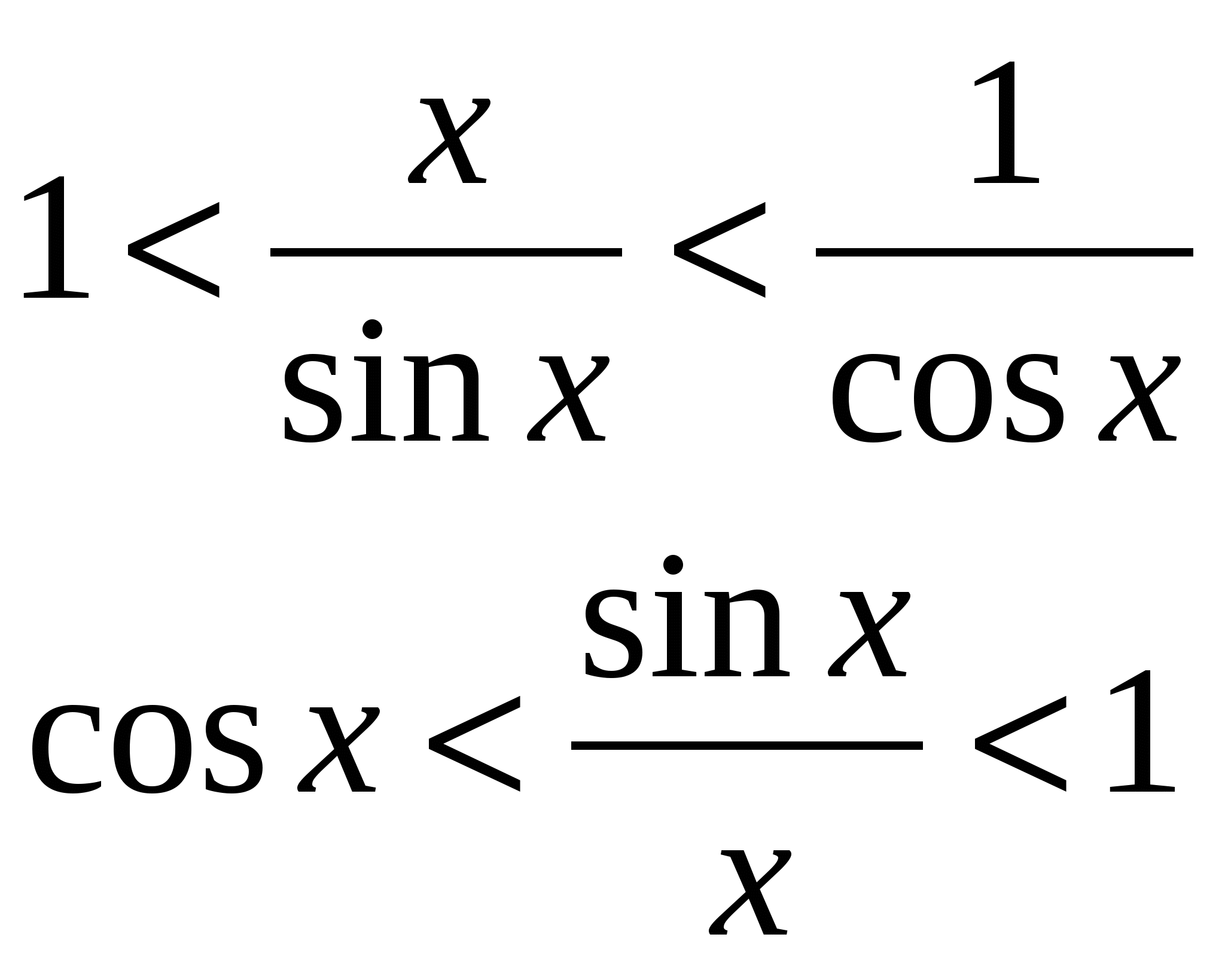 и получим: Т.к.  , то по признаку существования пределов следует .2 замечательный предел.  Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами: 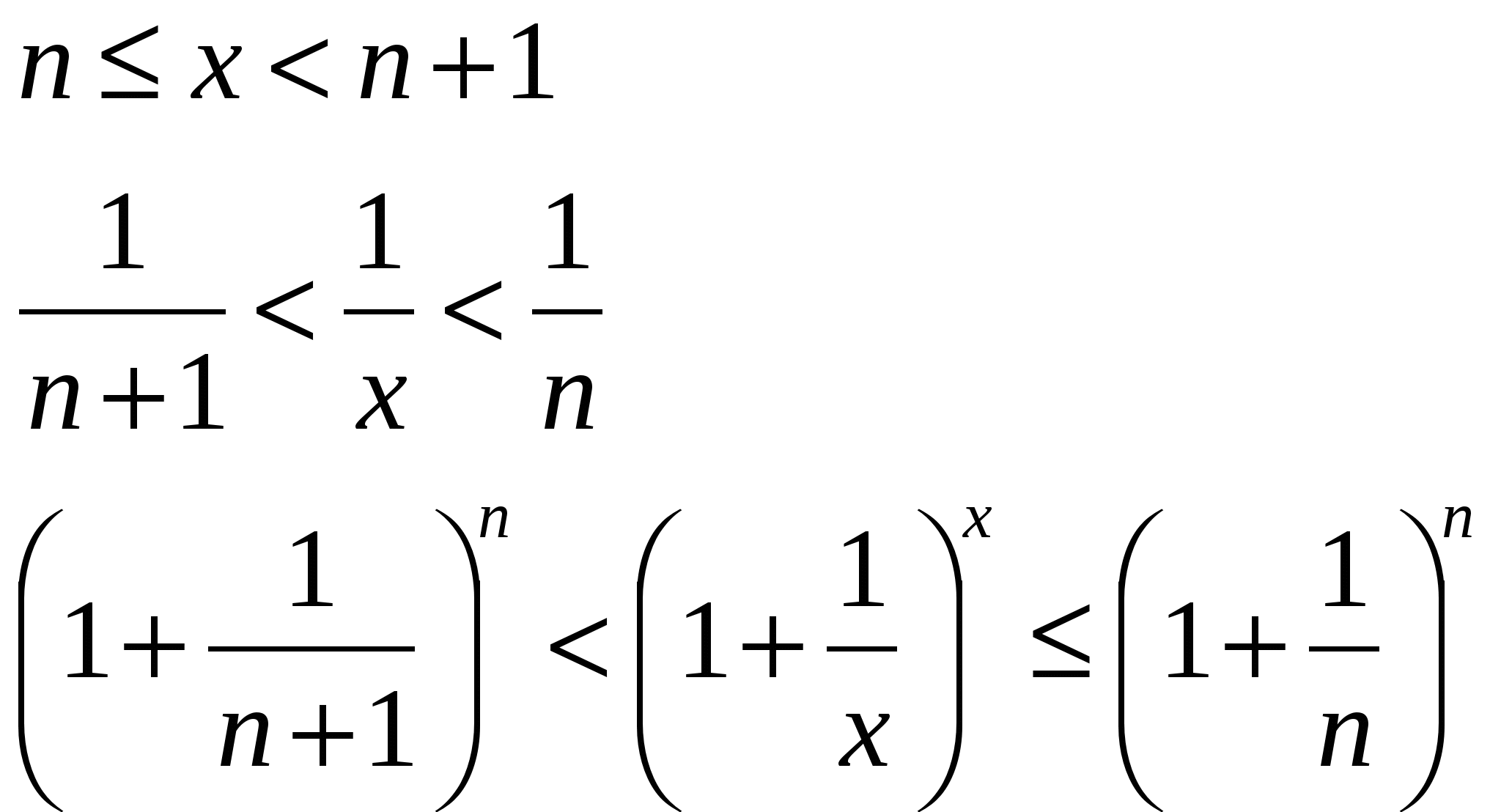 Если x→∞, то n→∞, тогда 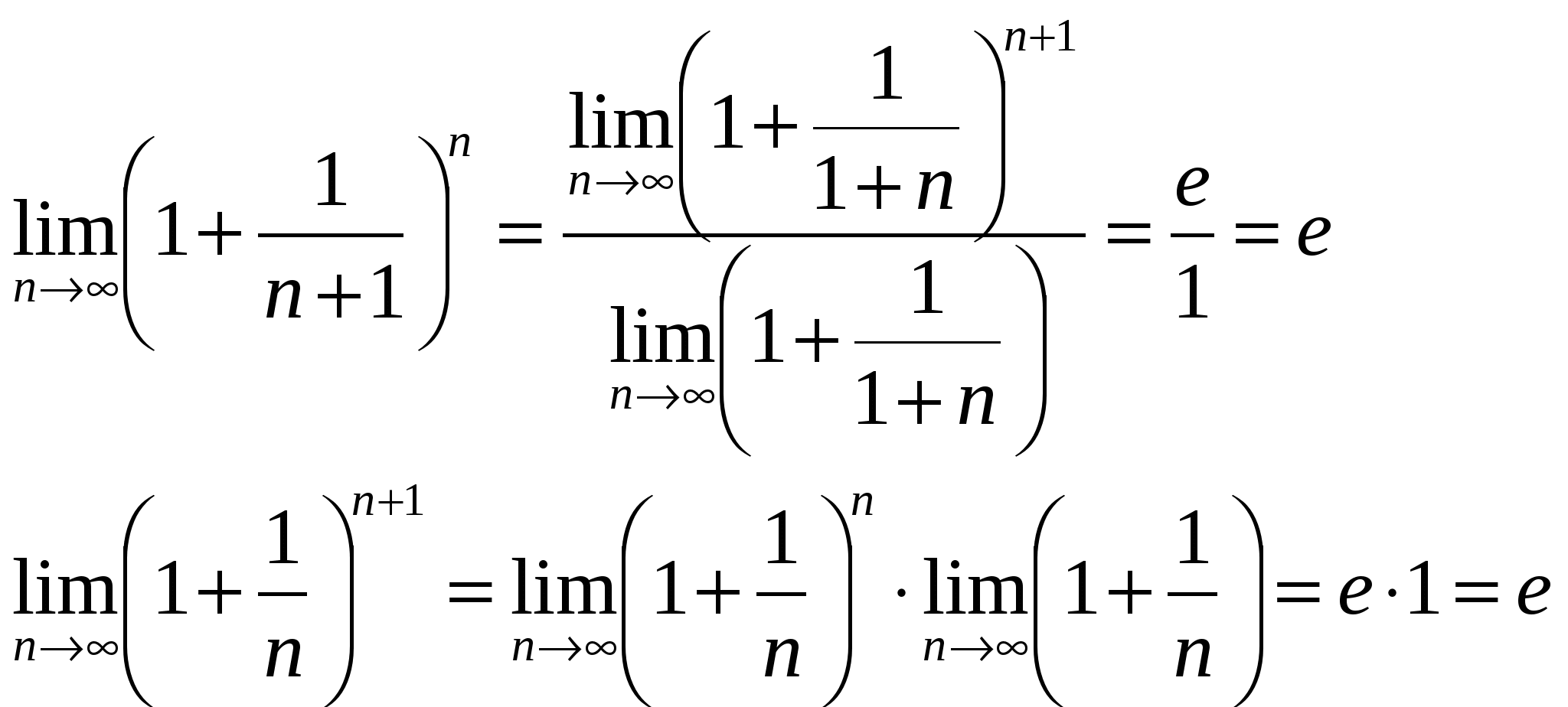 По признаку о существовании пределов: Вопрос9. Уравнение прямой проходящей через 2 данные точки. К (х1;у1) М (х2;у2) 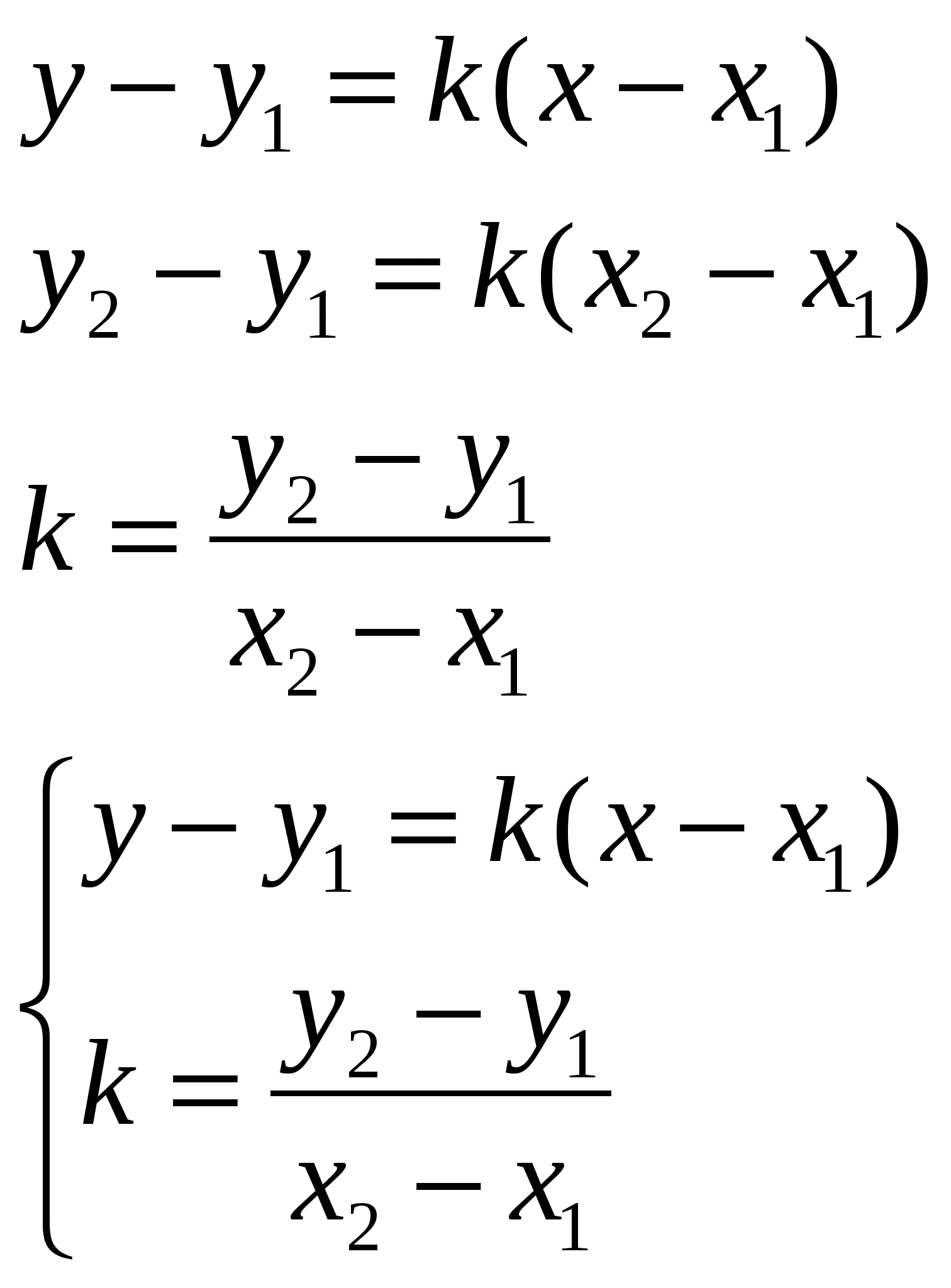  Вопрос8. Уравнение прямой с угловым коэффициентом.  k= tg α – угловой коэффициент. Если b=0 то прямая проходит через начало координат. Уравнение примет вид  Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.  Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет вид  и пройдет параллельно оси оу.Вопрос 10. Уравнение прямой в отрезках. К (а;0); М (0;b) Подставим точки в уравнение прямой:   Вопрос 11. Общее уравнение прямой.  A, B, C – произвольные числа, причем А и В не равны нулю одновременно.
Вопрос 19. Предел функции. Основные теоремы о пределах. Определение предела числовой функции. Односторонние пределы. Свойства пределов. Число А называется пределом функции y=f(x) в точке х0, если для любой последовательности допустимых значений аргумента xn, n€N (xn≠x0), сходящейся к х0 (т.е.  ), последовательность соответствующих значений функции f(xn), n€N, сходится к числу А, т.е.  . Геометрический смысл предела этой функции, что для всех точек х, достаточно близких к точке х0, соответствующие значения функции как угодно мало отличается от числа А.Односторонние пределы. Считается, что х стремится к х0 любым способом: оставаясь меньшим, чем х0 (слева от х0), большим, чем х0 (справа от х0), или колеблясь около точки х0. Число А1 называется пределом функции y=f(x) слева в точке х0, если для любого ε<0 существует число σ=σ(ε)>0 такое, что при х€(x0-σ;x0), выполняется неравенство |f(x)-A1|<ε   Пределом функции справа называется  Свойства пределов. 1) если предел  функция равна этому числу плюс б.м. ε – сколь угодно малое число |f(x)-a|=α; f(x)=a+ α 2) сумма конечного числа б.м. чисел есть б.м. число 3) предел произведения равен произведению пределов 4) константы можно выносить за знак предела 5)  Вопрос 21. Непрерывность функции. Точки разрыва. Свойства функций непрерывных на отрезке. Непрерывные функции и их свойства. Точка разрыва функций и их классификация. Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке:  Это означает: - функция определена в точке х0 и в ее окрестности; - функция имеет предел при х→х0 - предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство. Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0 Точки разрыва функции – это точки в которых нарушается непрерывность функции. Точка разрыва х0 называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)  и  При этом, если: - А1=А2 то точка х0 называется точкой устранимого разр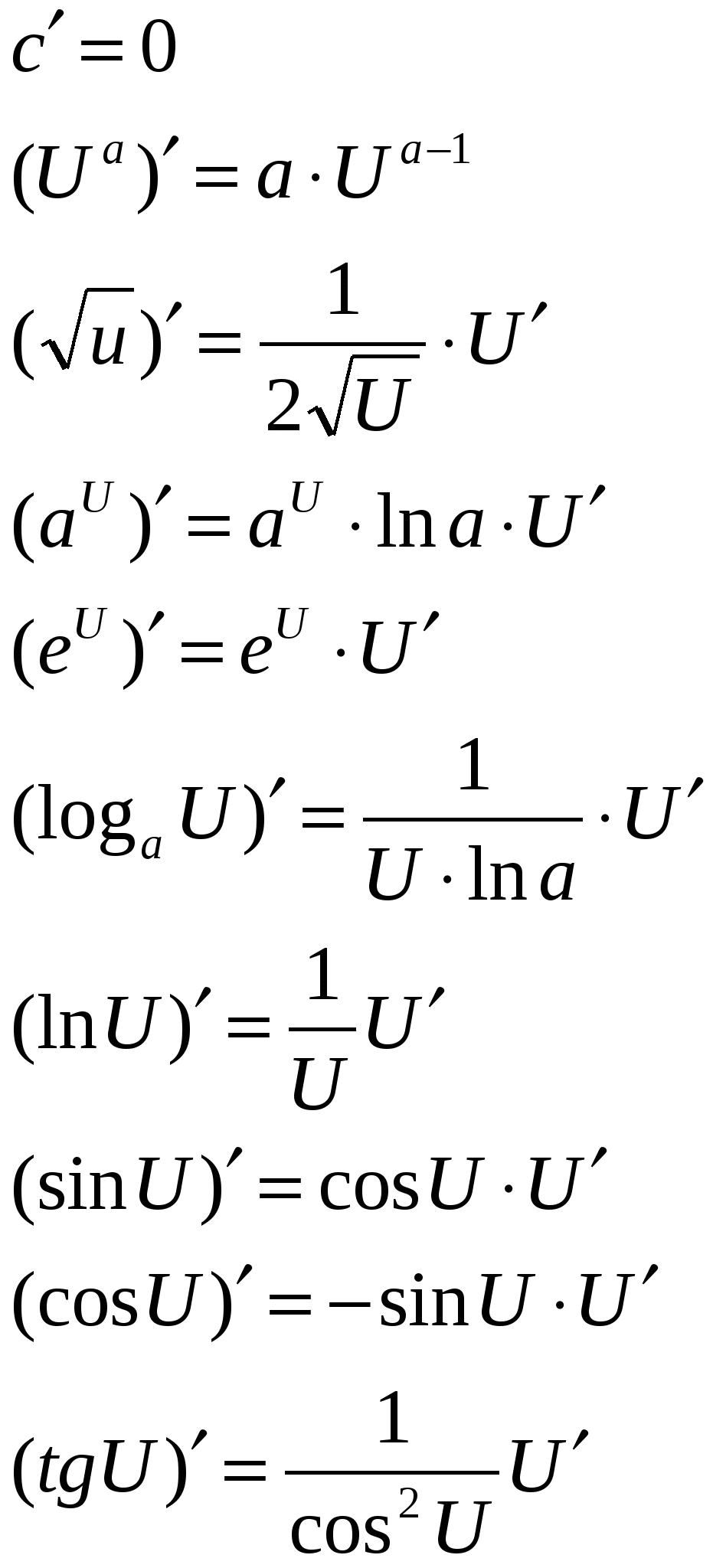ыва; -  А1≠А2 то точка х0 называется точкой конечного разрыва.|A1 – A2| называется скачком функции. Точка разрыва х0 называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности. |
или 
. Это уравнение прямой, параллельной оси оу. и проходящей через точку 
.
. Это уравнение прямой, параллельной оси ох.