|
|
1. Матрицы. Линейные операции над ними и их свойства
Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого:
Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В).
Следствие. Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей этих событий:
Р (АВ) = Р(А) · Р(В).
Следствие. При производимых n одинаковых независимых испытаниях, в каждом из которых событияА появляется с вероятностью р, вероятность появления события А хотя бы один раз равна 1 - (1 - р)n
Вопрос 43. Формула полной вероятности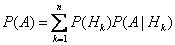 , где - полная группа гипотез, то есть , - достоверное событие. Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез. Формулировка Пусть дано вероятностное пространство , и полная группа событий , где - полная группа гипотез, то есть , - достоверное событие. Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез. Формулировка Пусть дано вероятностное пространство , и полная группа событий 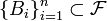 , таких что , таких что 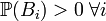 . Пусть суть интересующее нас событие. Тогда . Пусть суть интересующее нас событие. Тогда 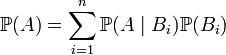 Замечание Формула полной вероятности также имеет следующую интерпретацию. Пусть N - случайная величина, имеющая распределение Замечание Формула полной вероятности также имеет следующую интерпретацию. Пусть N - случайная величина, имеющая распределение 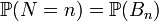 .Тогда .Тогда 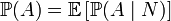 ,т.е. априорная вероятность события равна среднему его апостериорной вероятности. ,т.е. априорная вероятность события равна среднему его апостериорной вероятности.
Вопрос 44.Формула Бернулли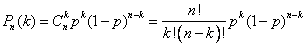 - вероятность появления события ровно раз при независимых испытаниях, - вероятность появления события при одном испытании.Формула Бернулли — формула в теории вероятности, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу. - вероятность появления события ровно раз при независимых испытаниях, - вероятность появления события при одном испытании.Формула Бернулли — формула в теории вероятности, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.
Формулировка. Теорема:Если Вероятность ρ наступления события Α в каждом испытании постоянна, то вероятность Pk,n того, что событие A наступит k раз в nнезависимых испытаниях, равна: 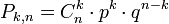 где q = 1-p Доказательство Пусть в результате n независимых испытаний, проведенных в одинаковых условиях, событие A наступает с вероятностью , следовательно противоположное ему событие с вероятностью где q = 1-p Доказательство Пусть в результате n независимых испытаний, проведенных в одинаковых условиях, событие A наступает с вероятностью , следовательно противоположное ему событие с вероятностью 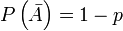 . Обозначим Ai — наступление события A в испытании с номером i. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате n опытов событие A наступает k раз, тогда остальные n − k − раз это событие не наступает. Событие A может появиться k раз в n испытаниях в различных комбинациях, число которых равно количеству сочетаний из n элементов по k. Это количество сочетаний находится по формуле: . Обозначим Ai — наступление события A в испытании с номером i. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате n опытов событие A наступает k раз, тогда остальные n − k − раз это событие не наступает. Событие A может появиться k раз в n испытаниях в различных комбинациях, число которых равно количеству сочетаний из n элементов по k. Это количество сочетаний находится по формуле: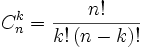 . При этом вероятность каждой комбинации равна произведению вероятностей: . При этом вероятность каждой комбинации равна произведению вероятностей: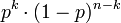 . Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли: . Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли: 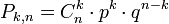 где q = 1-p где q = 1-p
Вопрос 45.
Определение случайной величины. Дискретные и непрерывные случайные величины.
Характеристи́ческая фу́нкция случа́йной величины́— один из способов заданияраспределения. Характеристические функции могут быть удобнее в тех случаях, когда, например,плотностьилифункция распределенияимеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросовслабой сходимости (сходимости по распределению).Пусть естьслучайная величинаXс распределением. Тогда характеристическая функция задаётся формулой: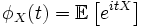 .Пользуясь формулами для вычисленияматематического ожидания, определение характеристической функции можно переписать в виде: .Пользуясь формулами для вычисленияматематического ожидания, определение характеристической функции можно переписать в виде: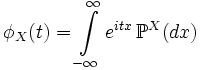 ,то есть характеристическая функция — этообратное преобразование Фурьераспределения случайной величины. Если случайная величинаXпринимает значения в произвольномгильбертовом пространстве, то её характеристическая функция имеет вид: ,то есть характеристическая функция — этообратное преобразование Фурьераспределения случайной величины. Если случайная величинаXпринимает значения в произвольномгильбертовом пространстве, то её характеристическая функция имеет вид: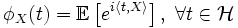 ,гдеобозначаетскалярное произведениев.[править]Дискретные и абсолютно непрерывные случайные величиныЕсли случайная величинаXдискретна, то есть ,гдеобозначаетскалярное произведениев.[править]Дискретные и абсолютно непрерывные случайные величиныЕсли случайная величинаXдискретна, то есть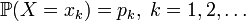 , то , то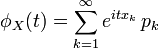 . Cвойства характеристических функций Характеристическая функция однозначно определяет распределение. ПустьX,Yсуть две случайные величины, и . Cвойства характеристических функций Характеристическая функция однозначно определяет распределение. ПустьX,Yсуть две случайные величины, и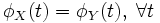 . Тогда. В частности, если обе величины абсолютно непрерывны, то совпадение характеристических функций влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение характеристических функций влечёт совпадение функций вероятности. Характеристическая функция всегда ограничена: . Тогда. В частности, если обе величины абсолютно непрерывны, то совпадение характеристических функций влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение характеристических функций влечёт совпадение функций вероятности. Характеристическая функция всегда ограничена: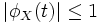 . Характеристическая функция в нуле равна единице: . Характеристическая функция в нуле равна единице: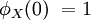 . Характеристическая функция всегданепрерывна: . Характеристическая функция всегданепрерывна: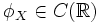 . Характеристическая функция как функция случайной величины однородна: . Характеристическая функция как функция случайной величины однородна: 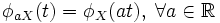 . Характеристическая функция суммынезависимыхслучайных величин равна произведению их характеристических функций. Пустьсуть независимые случайные величины. Обозначим . Характеристическая функция суммынезависимыхслучайных величин равна произведению их характеристических функций. Пустьсуть независимые случайные величины. Обозначим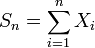 . Тогда . Тогда 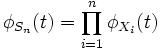 . Вопрос 46.Законы распределения случайной величины.Законы распределения случайных величин.Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно. Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать. Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы. Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, ..., хn с соответствующими им вероятностями р1, р2, ..., рn: . Вопрос 46.Законы распределения случайной величины.Законы распределения случайных величин.Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно. Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать. Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы. Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, ..., хn с соответствующими им вероятностями р1, р2, ..., рn:
Вопрос 47.Математическое ожидание, дисперсия, среднее квадратическое отклонение дискретной случайной величины. Дискретные случайные величины
xi - значения величины X, 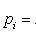 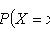 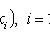 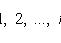 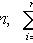 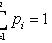
Математическое ожидание Математи́ческое ожида́ние — понятие среднего значения случайной величины в теории вероятностей. В зарубежной литературе обозначается через , в русской M[X]. В статистике часто используют обозначение μ.
Пусть задано вероятностное пространство и определённая на нём случайная величина X. То есть, по определению, —измеримая функция. Тогда, если существует интеграл Лебега от X по пространству Ω, то он называется математическим ожиданием, или средним значением и обозначается M[X] или .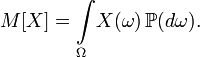 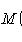 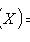 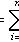 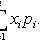
Свойства: 1) M(C) = C, C - постоянная; 2) M(CX) = CM(X); 3) M(X1 + X2) = M(X1) + M(X2), где X1, X2 - независимые случайные величины; 4) M(X1X2) = M(X1)M(X2).
Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается D[X]в русской литературе и (англ. variance) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.Из неравенства Чебышёва следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75% случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89% — не более чем на три. Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда 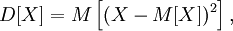 где символ M обозначает математическое ожидание. Свойства: 1) D(C) = 0; 2) D(CX) = C2D(X); 3) D(X1 + X2) = D(X1) + D(X2), где символ M обозначает математическое ожидание. Свойства: 1) D(C) = 0; 2) D(CX) = C2D(X); 3) D(X1 + X2) = D(X1) + D(X2),
где X1, X2 - независимые случайные величины.
Среднее квадратическое отклонение случайной величины Х Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.
Вопрос 48
.Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины: 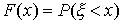
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х.
Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.
Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству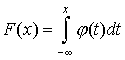
|
|
|
|
 Скачать 0.98 Mb.
Скачать 0.98 Mb.