1. Матрицы. Линейные операции над ними и их свойства

• Название: 1. Матрицы. Линейные операции над ними и их свойства
• Дата: 11.10.2018
• Размер: 0.98 Mb.
• Имя файла: MATEMATIKA (1).doc
• Тип: Документы; #53131
• страница: 2 из 4

Вопрос 22. Правила дифференцирования. Производные элементарных функций.

Производная от функции. Дифференцируемость функции. Дифференциал.

Производной функции y=f(x) в точке х₀ называется предел отношения приращения функции к приращению аргумента, когда аргумент стремится к нулю.



Производная функции f(x) есть некоторая функция

f ’(x), произведенная из данной функции.

Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале.

Операция нахождения производной называется дифференцированием.

Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).

Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Правила дифференцирования суммы, произведения, частного функции. Производные сложных функций.

Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Производная обратной функции равна обратной величине производной данной функции.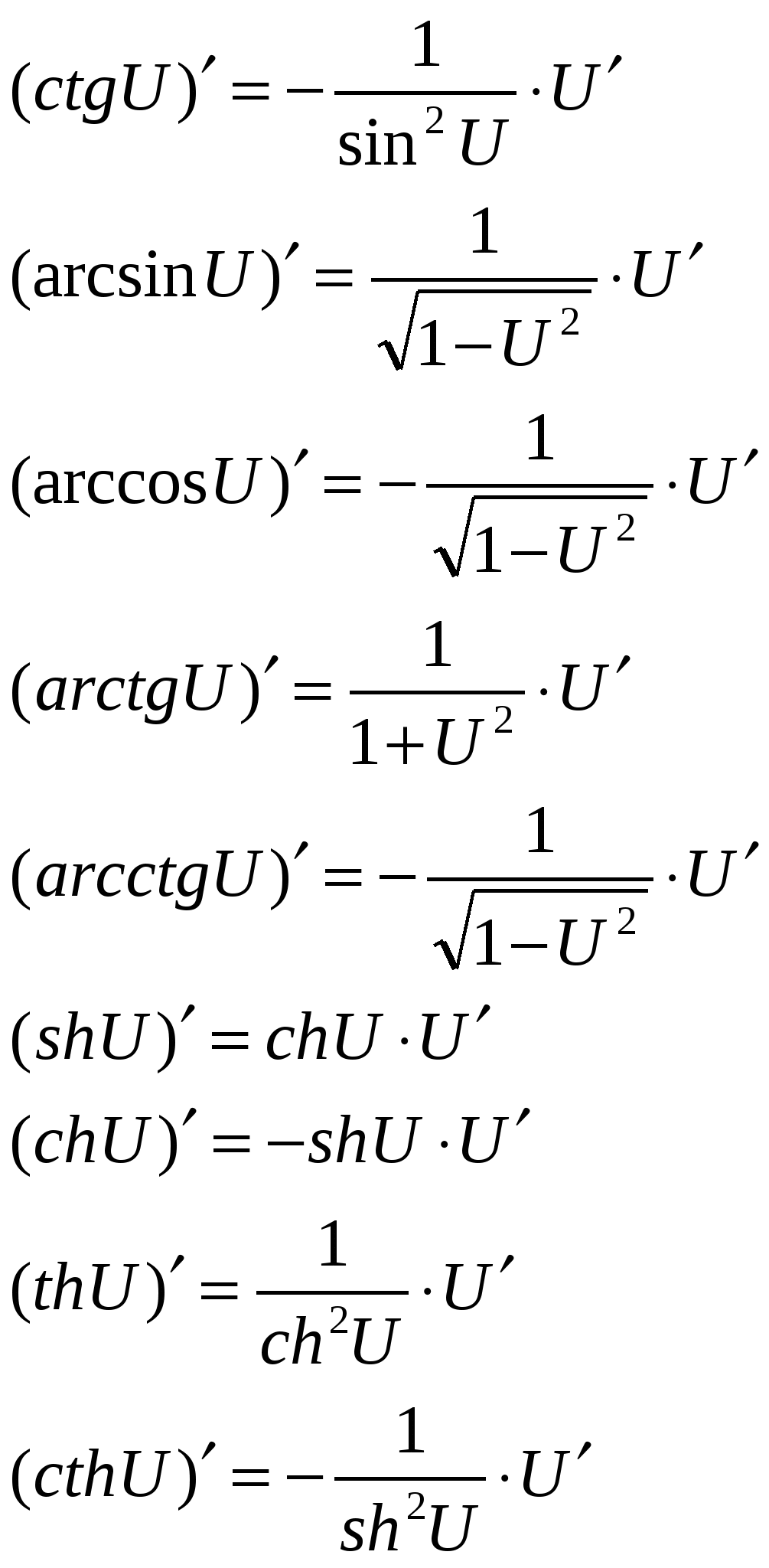

Вопрос 23. Дифференциал ф-ии. Геометрический смысл дифференциала.

Операция нахождения производной называется дифференцированием.

Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).

Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Вопрос 24.производные и дифференциалы высших порядков.

Дифференциалы высших порядков.

Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференциал этой функции. Дифференциал от дифференциала есть второй дифференциал.

Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Вопрос 25. Правило лопиталя. Правило Лопиталя. Рассмотрим способ раскрытия неопределенностей 0 / 0 и ∞ / ∞, который основан на применении производных.

Правило Лопиталя, при 0 / 0.Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ и обращается в нуль в этой точке: Пусть φ ′(x) ≠ 0 в окрестности точки x₀ Если существует предел, то

Применим к функциям f(x) и φ(x) теорему Коши для отрезка [x₀;x], лежащего в окрестности точки x₀ , тогда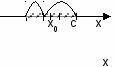

, где с лежит между x₀ и х.

При x→x₀ величина с также стремится к х₀; перейдем в предыдущем равенстве к пределу:



Так как , то .

Поэтому

(предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует) Правило Лопиталя, при ∞ / ∞. 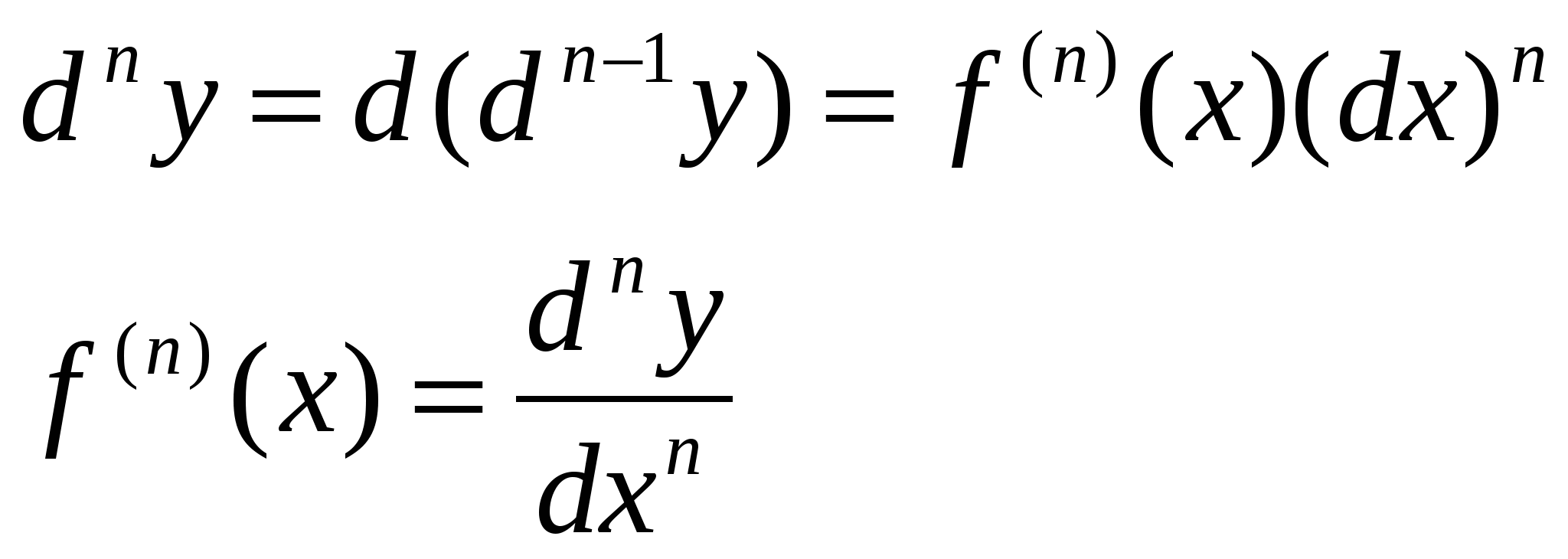Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ (кроме точки x₀), в этой окрестности 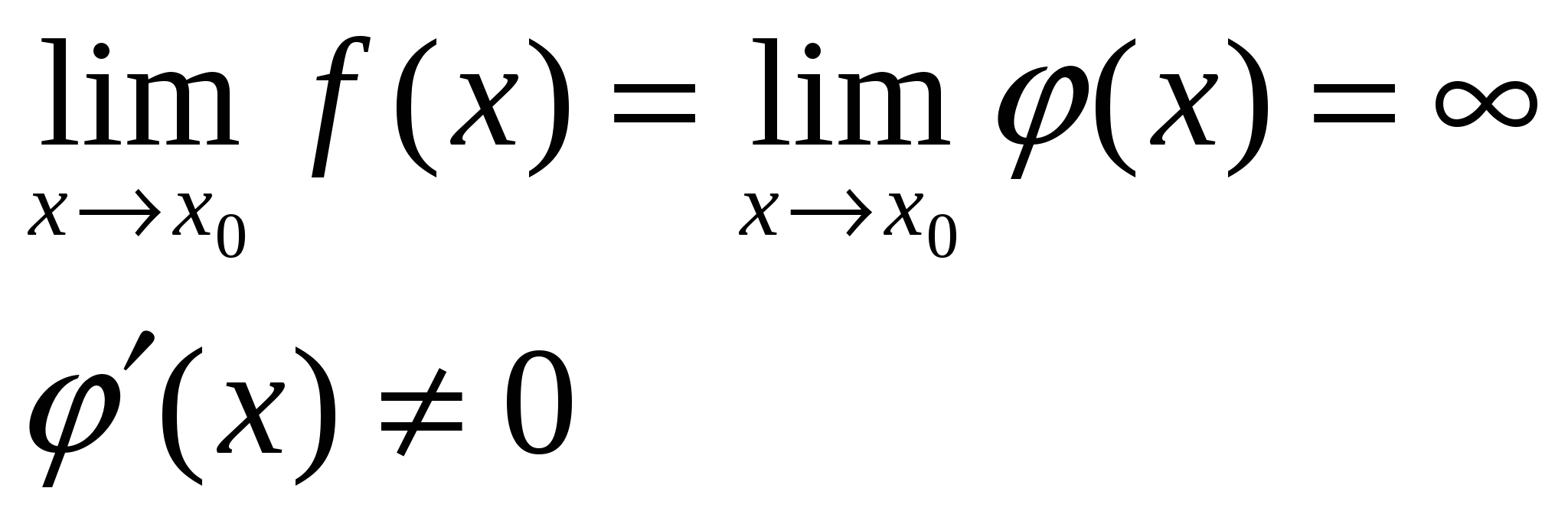Если существует предел, то

Неопределенности вида 0∙∞ ; ∞-∞ ; 1^∞ ; ∞⁰ ; 0⁰ сводятся к двум основным. Например, 0∙∞ Пусть f(x)→0, φ(x)→∞ при х→х<s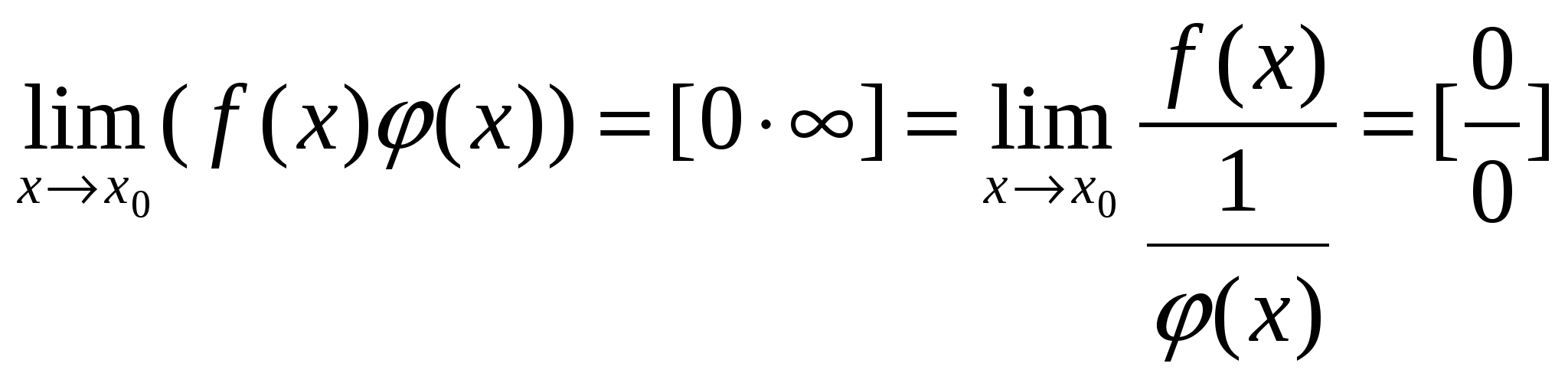ub>0

Вопрос 29.</sub>

Исследование условий и построение графиков.

- найти область определения функции

- найти точки пересечения графика с осями координат

- найти интервалы знака постоянства

- исследовать на четность, нечетность

- найти асимптоты графика функции

- найти интервалы монотонности функции

- найти экстремумы функции

- найти интервалы выпуклости и точки перегиба

Вопрос 11.Общие уравнения прямой.


     Общее уравнение Ax + By + C (> 0).   Вектор = (А; В) - нормальный вектор прямой.

     В векторном виде: + С = 0, где  - радиус-вектор произвольной точки на прямой (рис. 4.11).     Частные случаи:     1) By + C = 0 - прямая параллельна оси Ox;      2) Ax + C = 0 - прямая параллельна оси Oy;      3) Ax + By = 0 - прямая проходит через начало координат;     4) y = 0 - ось Ox;     5) x = 0 - ось Oy.

Вопрос 13 угол между прямыми.

 Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом y = k₁x + B₁,         y = k₂x + B₂,     то угол между ними  определяется по формуле      (5) Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой. Если уравнения прямой заданы в общем виде A₁x + B₁y + C₁ = 0,         A₂x + B₂y + C₂ = 0,     (6) угол между ними определяется по формуле     (7)

Вопрос 12. Уравнение прямой проходящей через данную точку в заданном направлении. 1. Уравнение прямой, проходящей через данную точку A(x₁, y₁) в данном направлении, определяемом угловым коэффициентом k, y - y₁ = k(x - x₁).     (1) Это уравнение определяет пучок прямых, проходящих через точку A(x₁, y₁), которая называется центром пучка.

Вопрос 14 Взаимное расположение 2х прямых

Пусть сейчас оба уравнения прямых записаны в общем виде.

Теорема. Пусть

    и 

– общие уравнения двух прямых на координатной плоскости Оху. Тогда

1)если , то прямые  и  совпадают;

2)если , то прямые   и 

    параллельные;

3)если , то прямые пересекаются.

   Доказательство. Условие  равносильно коллинеарности нормальных векторов данных прямых:

. Поэтому, если , то  и прямыепересекаются.

   Если же , то , ,  иуравнение прямой  принимает вид:

 или , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.

   Если же прямые не совпадают и не пересекаются, то остается случай , т.е. прямые параллельны.

Теорема доказана.

   Заметим, что если прямые пересекаются, то для нахождения координатих точки пересечения достаточно решить систему двух уравнений сдвумя неизвестными:

                            .                               (4)

Следствие. Пусть  – определитель системы (4). Если , то прямые пересекаются в одной точке и система (4) имеет единственное решение, которое можно найти по формулам Крамера:

                                  ,                                (5)

где , .

Если , то прямые или параллельны и тогда система (4) не имеет решений, или прямые совпадают и тогда система (4) имеет бесконечно много решений.

   Доказательство. По определению определителя второго порядка

                      .

Если , то  и , т.е. прямые пересекаются икоординаты точки пересечения можно найти по формулам Крамера (5).

Если же , то  и , т.е. либо прямые параллельны и тогда система не может иметь ни одного решения, либо прямыесовпадают и тогда система (4) состоит из одного уравнения и решениями такой системы являются координаты любой точки, лежащей на прямой, а их бесконечно много.

следствие доказано.

Вопрос 15.

Нормальное уравнение прямой

    Нормальное уравнение прямой (рис. 4.11) где  - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.     Приведение общего уравнения прямой к нормальному виду: Здесь  - нормируемый множитель прямой; знак выбирается противоположным знаку C, если  и произвольно, если C = 0.

Вопрос 17.

Функции. Способы задания и свойства функций.

Функция- зависимость переменной у от переменной x, есликаждому значению х соответствует единственное значение у. Переменная х- независимая переменная или аргумент. Переменная у- зависимая переменная Значение функции- значение у, соответствующее заданному значению х. Область определения функции- все значения, которые принимает независимаяпеременная. Область значений функции (множество значений)- все значения, которые принимает функция. Функция является четной- если для любого х из области определенияфункции выполняется равенство f(x)=f(-x) Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x) Возрастающая функция- если для любых х₁ и х₂, таких, что х₁< х₂, выполняетсянеравенство f(х₁)₂) Убывающая функция- если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)>f(х₂) Способы задания функции. Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции.

Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически. На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для

имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

Виды функций и их свойства

1) Постоянная функция- функция, заданная формулой у=b, где

b-некоторое число. Графиком постоянной функции у=b является прямая,

параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат

2) Прямая пропорциональность- функция, заданная формулой у=kx,

где к¹0. Число k называется коэффициентом пропорциональности

Вопрос 18. Предел числовой последовательности.

Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу  a  при увеличении порядкового номера  n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение:«Число называется пределом числовой последовательности (Un)предел Un при n стремящимся к бесконечности равно какому то числу a, если для любого ξ найдется такое число N = N(ξ), зависящее от ξ, что | Un -а|< ξ при n>N».

Это определение означает, что  a  есть предел числовой последовательности, если её общий член неограниченно приближается к  a  при возрастании  n. Геометрически это значит, что для любого  > 0  можно найти такое число N,  что начиная с  n > N  все члены последовательности расположены внутри интервала ( a a  ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.Последовательность называется ограниченной, если существует такое число M, что | u_n  | Mдля всех  n .Возрастающая или убывающая последовательность называется монотонной. Основные свойства пределов.Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций. Если { u_n } и { v_n }  две сходящиеся последовательности, то: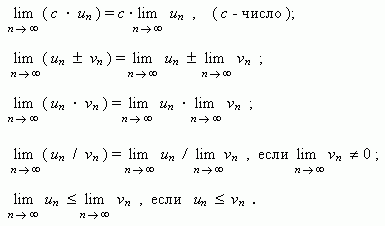

Если члены последовательностей { u_n}, { v_n},{ w_n}удовлетворяют неравенствам
 Некоторые замечательные пределы.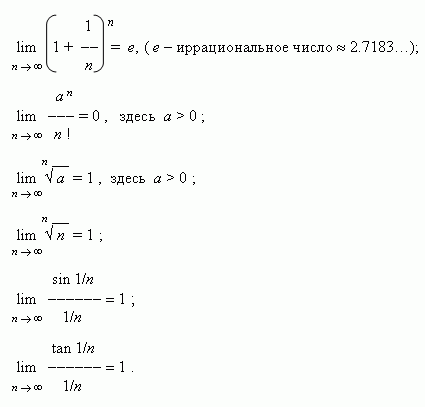 

Вопрос 26.

Возрастание и убывание функций. Экстремумы функций.

Рассмотрим приложение производной функции к исследованию поведения функции. По первой производной функции можно определить промежутки возрастания и убывания функции, а также определить точки экстремума функции (максимум и минимум).

Определение. Функция  называется возрастающей в точке  , если в некоторой  -окрестности этой точки справедливо



для любого  .

Определение. Функция  называется возрастающей на отрезке  , если для любых двух точек  справедливо неравенство



когда  .

Определение. Функция  называется убывающей в точке  , если в некоторой  -окрестности этой точки справедливо неравенство



для любого  .