Определение. Функция называется убывающей на отрезке , если для любых двух точек 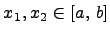 справедливо неравенство справедливо неравенство
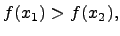
когда .
Определение. Функция имеет в точке максимум, если значение является наибольшим в некоторой двустороней окрестности точки .
Определение. Функция имеет в точке минимум, если значение является наименьшим в некоторой двусторонней окрестности точки .
Определение. Функция имеет в точке экстремум, если точка является точкоймаксимума или минимума.
Признаки (достаточные) возрастания и убывания функции :
Если на интервале , то функция возрастает на этом интервале;
Если на интервале , то функция убывает на этом интервале.
Необходимое условие экстремума функции.
Функция может иметь экстремум только в точках, где или производная не существует. Точка, где или производная не существует называется критической точкой.
Заметим, что если в точке выполняется, что , то это означает, что касательная в данной точке параллельная оси . Если производная в точке не существует, то это значит либо касательная вертикальная, либо ее нет в данной точке.
Достаточные условие экстремума функции.
Если функция непрерывна в точке и имеет в некоторой окрестности точки , кроме, быть может самой точки , конечную производную и если при переходе через точку :
меняет знак с '+' на '-', то точка -- точка максимума;
меняет знак с '-' на '+', то точка -- точка минимума;
не меняет знак, то точка не является точкой экстремума.
Вопрос 27.Исследование функции на выпуклость. Точки перегиба. Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в точке ( x0 ), и обозначаетсяf '' ( x0 ). Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x0, f ( x0 ) ), x0 ( a, b ). Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0, f ( x0 ) ), x0 ( a, b ). Достаточное условие вогнутости ( выпуклости ) функции. Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда: если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b ); если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкойперегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
Вопрос 28. Асимптоты.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Асимптотой кривой называется прямая, расстояние от которой до точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Асимптоты могут быть вертикальными, наклонными и горизонтальными. Говорят, что прямая является вертикальной асимптотой графика функции y = f (x), если , или , или . То есть, для отыскания вертикальных асимптот следует найти те значения х, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Для определения наклонной асимптотыy = kx + b числа k (угловой коэффициент прямой) и b находят из формул: , .Но если хотя бы один из этих пределов не существует или равен бесконечности, то кривая y = f (x) наклонных асимптот не имеет. Отметим, что следует отдельно рассмотреть случаи х + и х. Частным случаем наклонной асимптоты при k = 0 и будет горизонтальная асимптота. Поэтому y = b – уравнение горизонтальной асимптоты. Рассмотрим график функции на рис. 15. Точки х = х2, х = х4 – точки экстремумов функции, точка х = х1 – это точка перегиба. Точка х = х3 является особенной точкой для функции, в ней f(x) терпит разрыв, а прямая х = х3 является вертикальной асимптотой графика функции. Прямая y = kx + b тоже будет асимптотой графика, только наклонной, прямая у = 0 – горизонтальная асимптота графика. Если точка М(х, у) лежит на графике и неограниченно удаляется от начала координат, то она приближается к одной из этих прямых; расстояние от точки М(х, у) до асимптот стремится к нулю.
Вопрос 30.
Неопределенный интеграл и его свойства. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом 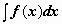 .Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то .Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то 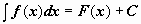 , где C - произвольная постоянная. Функциюf(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением. Неопределенный интеграл , где C - произвольная постоянная. Функциюf(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением. Неопределенный интеграл 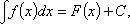 где F - первообразная функции f (на промежутке); C - произвольная постоянная. где F - первообразная функции f (на промежутке); C - произвольная постоянная.
Основные свойства 1. 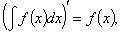 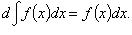
2.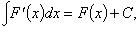 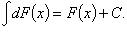
3. Если 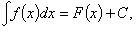 то то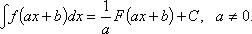
Вопрос 31. Определенный интеграл и его свойства. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], то 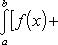 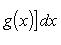 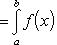 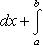 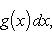 т. е. интеграл суммы равен сумме интегралов слагаемых. 2. Если f(x) - непрерывная функция, а c - постоянное число, то т. е. интеграл суммы равен сумме интегралов слагаемых. 2. Если f(x) - непрерывная функция, а c - постоянное число, то 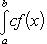 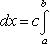 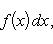 Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е. 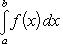 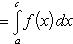 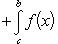 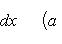 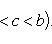 В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = xm, то В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = xm, то 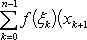 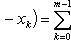 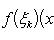 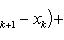 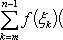 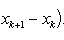 Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0. 4. Пусть функция f(x) непрерывна в промежутке [A, B]. Если a, b, c суть точки этого промежутка, то Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0. 4. Пусть функция f(x) непрерывна в промежутке [A, B]. Если a, b, c суть точки этого промежутка, то 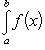 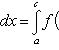 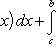 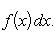 (13) В самом деле, если из точек a, b и c две (а тем более три) совпадают, то равенство (13) очевидно. Пусть же все эти точки различны. Если a < c < b, то дело сводится к теореме 3. Прочие случаи взаимного расположения точек a,b, c тоже легко свести к той же теореме. Пусть, например, c < b < a. Тогда (13) В самом деле, если из точек a, b и c две (а тем более три) совпадают, то равенство (13) очевидно. Пусть же все эти точки различны. Если a < c < b, то дело сводится к теореме 3. Прочие случаи взаимного расположения точек a,b, c тоже легко свести к той же теореме. Пусть, например, c < b < a. Тогда 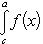 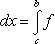 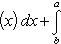 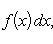 откуда откуда  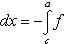 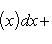 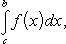 и остается дважды применить формулу (12). Свойство интеграла, выражаемое теоремами 3 и 4, называется аддитивностью его, как функции промежутка интегрирования. 5. Если f(x) - неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего*, то и сам интеграл будет числом неотрицательным и остается дважды применить формулу (12). Свойство интеграла, выражаемое теоремами 3 и 4, называется аддитивностью его, как функции промежутка интегрирования. 5. Если f(x) - неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего*, то и сам интеграл будет числом неотрицательным 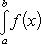 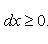 т. е. постоянный множитель можно выносить за знак интеграла. т. е. постоянный множитель можно выносить за знак интеграла.
Вопрос 32. Геометрический смысл определенного интеграла.
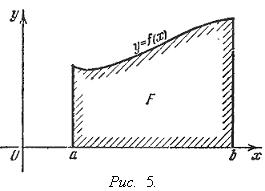
Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл
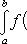  представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.). представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.).
 Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z1, z2, ...,zN. Составим для f(x) интегральную сумму σ. Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z1, z2, ...,zN. Составим для f(x) интегральную сумму σ.
Пусть из точек ξ0, ξ1, ..., ξn-1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f(zi) | (i = 1, 2, ..., N) естьK, то, очевидно,
| σ | ≤ Kpλ ≤ KNλ, откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл 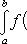 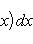 существует и равен нулю. Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так: существует и равен нулю. Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так:
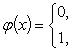 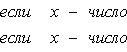 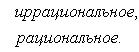 Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл 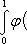 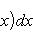 не существует. В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций. не существует. В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.
Вопрос 33.
Несобственные интегралы и их сходимость.
Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси 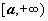 и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла 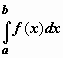 при при 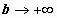 называется несобственным интегралом функции f(x) от a до называется несобственным интегралом функции f(x) от a до 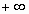 и обозначается и обозначается 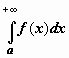 . .
Итак, по определению, 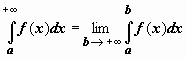 . Если этот предел существует и конечен, интеграл . Если этот предел существует и конечен, интеграл 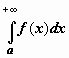 называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся. называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
Вопрос 34.
Числовые ряды.
Признаки сходимости. Пусть задана бесконечная последовательность чисел . Выражение
называется числовым рядом. Числа называются членами этого ряда. Член ряда (97), стоящий на -м месте, считая от начала, называется общим членом этого ряда. Ряд (97) считается заданным, если известен общий член его, выраженный как функция номера .
Выражение (97) удобно обозначать следующим образом: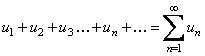 .Сумма конечного числа n первых членов ряда называетсяn-ой частичной суммой ряда. Рассмотрим частичные суммы: .Сумма конечного числа n первых членов ряда называетсяn-ой частичной суммой ряда. Рассмотрим частичные суммы: 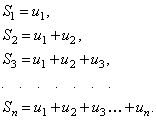 Если существует конечный предел , то его называют суммой ряда (97) и говорят, что ряд (97) сходится. Если не существует (например , при ), то говорят, что ряд (97) расходится и суммы не имеет,an>0 . ряд. Если существует конечный предел , то его называют суммой ряда (97) и говорят, что ряд (97) сходится. Если не существует (например , при ), то говорят, что ряд (97) расходится и суммы не имеет,an>0 . ряд.
Признак Даламбера: , ,
если d <1 — ряд сходится, если d >1 — ряд расходится,
если d =1 — о сходимости или расходимости ряда судить нельзя.
Признак Коши: , ,
если c <1 — ряд сходится, если c >1 — ряд расходится,
если c =1 — о сходимости или расходимости ряда судить нельзя.
Знакочередующийся ряд: , .
Если сходится ряд , то ряд — сходится а б с о л ю т н о.
Если ряд расходится, а ряд сходится, то знакочередующийся ряд
— сходится у с л о в н о.
Признак Лейбница:
если an монотонно убывая стремится к нулю, то ряд сходится и
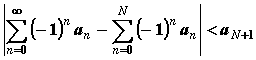 . .
Вопрос 35. Основные понятия о дифференциальных уравнениях.
Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида F (x, y(x), y '(x), y ''(x), … , y(n)(x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения. Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество. Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме: y(n) = f(x, y, y ', y '', … , y(n − 1)).
|
Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x0) = y0, y'(x0) = y1, y ''(x0) = y2, … , y(n − 1)(x0) = yn − 1.
|
Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения
F(x, y(x), y '(x), y ''(x), … , y(n )(x)) = 0, x>x0,
удовлетворяющего условиям
y(x0) = y0, y '(x0) = y1, y ''(x0) = y2, … , y(n − 1)(x0) = yn − 1.
Условия y(x0) = y0, y '(x0) = y1, y ''(x0) = y2, … , y(n − 1)(x0) = yn − 1 называются начальными данными, начальными условиями или данными Коши.
Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x), … , y(n )(x)) = 0, называетсячастным решением.
Вопрос 36.
Дифференциальные уравнения с разделяющимися переменными.
Определение и способ решения
Пусть y(x) — некоторая функция, y'(x) — ее производная. Для удобства будем записывать производную виде 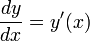 , имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал dx — приращение значения переменной в окрестности x, стремящееся к нулю. Дифференциал функции dy — малое приращение функции, dy = f(x + dx) − f(x) = y'(x)dx. Пусть f(x) и g(y) — некоторые функции от x и y. Рассмотрим уравнение , имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал dx — приращение значения переменной в окрестности x, стремящееся к нулю. Дифференциал функции dy — малое приращение функции, dy = f(x + dx) − f(x) = y'(x)dx. Пусть f(x) и g(y) — некоторые функции от x и y. Рассмотрим уравнение 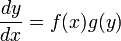 . Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на : . Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на : 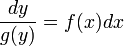 . Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при x = x0 y = y0 и возьмем интегралы от левой и правой частей. Пределы интегрирования — от y0 до y для левой части и от x0 для x для правой части уравнения: . Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при x = x0 y = y0 и возьмем интегралы от левой и правой частей. Пределы интегрирования — от y0 до y для левой части и от x0 для x для правой части уравнения: 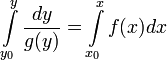 Решая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить y(x). Значения x0 и y0 называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных — Решая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить y(x). Значения x0 и y0 называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных — 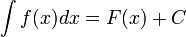 , где F(x) — первообразная f(x), C — произвольная постоянная, запишем это в виде , где F(x) — первообразная f(x), C — произвольная постоянная, запишем это в виде
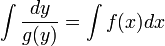 .Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные y, удовлетворяющие уравнению g(y) = 0. При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю). .Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные y, удовлетворяющие уравнению g(y) = 0. При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).
Вопрос 37.
Однородные дифференциальные уравнения.
Существует два понятия однородности дифференциальных уравнений.
1 Обыкновенное уравнение первого порядка 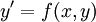 называется однородным относительно x и y, если функция является однородной степени 0: называется однородным относительно x и y, если функция является однородной степени 0: 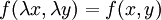 . Однородную функцию можно представить как функцию от : . Однородную функцию можно представить как функцию от : 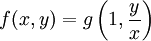 . С помощью подстановки (так как . С помощью подстановки (так как 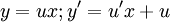 ) дифференциальное уравнение ) дифференциальное уравнение 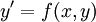 сводится к уравнению с разделяющимися переменными: сводится к уравнению с разделяющимися переменными:
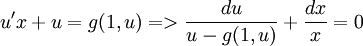 . .
2 Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение 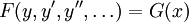 — однородно, если — однородно, если 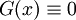 . В случае, если . В случае, если 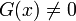 , говорят о неоднородном дифференциальном уравнении. Именно для решения линейных однородных диф. уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции. , говорят о неоднородном дифференциальном уравнении. Именно для решения линейных однородных диф. уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции.
Вопрос 38.
линейные дифференциальные уравнения первого ,второго порядка.
обыкновенным дифференциальным уравнением первого порядка называется уравнение
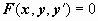 ; ;
|
(5)
|
где x - независимая переменная, y(x) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:
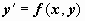 ; ;
|
(6)
|
Если пользоваться другим обозначением производной, то можно записать (6) как
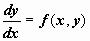 ; ;
|
(7)
|
Общее решение (общий интеграл) уравнения при n = 1 имеет вид 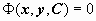 или или 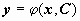 . .
Вопрос39.Частные производные функции нескольких переменных. Полный дифференциал..
Пусть функция у = f(X) определена в некоторой окрестности точки Х0.
Если зафиксировать все переменные, кроме xi, получим функцию одной переменной xi:
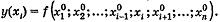
Производная функции y(xi) в точке xi = xi0 называется частной производной функции у = f(X) в точке Х0 по переменной xi.
Обозначение: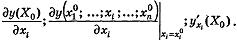
Определение 11. Линейные функции 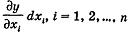 переменных dxi называются частными дифференциалами функции у = f(X). переменных dxi называются частными дифференциалами функции у = f(X).
Обозначение: dxiy
Определение 12. Функция у = f(X) называется дифференцируемой в точке Х0, если существуют числа A1, А2,..., Аn такие, что полное приращение функции имеет вид:
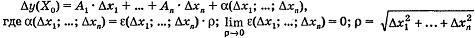
При этом линейная часть приращения A1 • 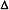 x1 + ... + Аn • x1 + ... + Аn • 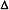 xn называется полным дифференциалом функции f(X) в точке Х0. xn называется полным дифференциалом функции f(X) в точке Х0.
Теорема 2. Если функция f(X) дифференцируема в точке Х0, то ее полный дифференциал в этой точке имеет вид:
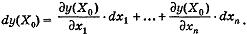
Замечание. При расчете частных производных необходимо помнить следующее.
1. Все правила вычисления производных и все табличные производные функций одной переменной сохраняют силу.
2. При частном дифференцировании функции z = f(x; у) по переменной х переменную у считаем фиксированной, т. е. константой. Поэтому, в частности, производная по х от любого выражения, зависящего только от у, равна 0. Например,
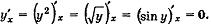
И вообще, (f(y))'x = 0.
В произведении любой множитель, зависящий только от y, выполняет роль множителя-константы. Например,
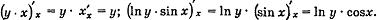
И вообще, (f(y) • g(x))'x = f(y) • g'(x). Дифференциа́л (от лат. differentia — разность, различие) в математике — линейная часть приращения функции или отображения. Это понятие, тесно связанное с понятием производной по направлению. ДИФФЕРЕНЦИАЛ – линейная часть приращенияфункции. Пусть функция y = f(x) дифференцируема на отрезке [a,b]. Производная этой функции в некоторой точке x отрезка [a,b] определяется равенством Отношение  стремится к определенному числу f (x)и, следовательно, отличается от производной f(x)на величину бесконечно малую: где a 0 при x 0. Умножение всех членов последнего равенства на x дает y = f(x) + ax.Так как, то приращение y функции состоит из двух слагаемых, из которых первое слагаемое есть (при f (x) 0) так называемая главная часть приращения, линейная относительноx. Произведение f (x)x называют дифференциалом функции и обозначают через dy или df(x):dy = f (x)x Можно найти дифференциал функции y = x. В этом случае y = (x) = 1и, следовательно,Dy = dx =x. Таким образом, дифференциал dx независимой переменной x совпадает с ее приращением стремится к определенному числу f (x)и, следовательно, отличается от производной f(x)на величину бесконечно малую: где a 0 при x 0. Умножение всех членов последнего равенства на x дает y = f(x) + ax.Так как, то приращение y функции состоит из двух слагаемых, из которых первое слагаемое есть (при f (x) 0) так называемая главная часть приращения, линейная относительноx. Произведение f (x)x называют дифференциалом функции и обозначают через dy или df(x):dy = f (x)x Можно найти дифференциал функции y = x. В этом случае y = (x) = 1и, следовательно,Dy = dx =x. Таким образом, дифференциал dx независимой переменной x совпадает с ее приращением
Вопрос 40.
Основные понятия комбинаторики.
Комбинаторика изучает количество комбинаций подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятности часто используют формулы комбинаторики. 1)"Перестановками" называют комбинации, сост из одних и тех же n различен эл-тов и отличающихся только порядком их расположения. Число всех возможных перестановок Pn=n! 2)"Размещениями" называют комбинации, сост-е из n различн эл-тов по m эл-тов, либо их порядком. Число всех возможных размещений Amn=n*(n-1)*(n-2)...(n-m+1) 3)"Сочетанием" наз-т комбинации, сост-е из различных эл-тов по m эл-тов, кот. отличаются хотя бы одном эл-том. Число сочетаний Cmn=n!/(m!(n-m)!) Подчеркиваем, что числа размещений, перестановок и сочетаний связаны равенством Amn=Pm*Cmn
Вопрос 41.
Основные формулы для вычисления вероятностей.
I. Случайные события. 1. Основные формулы комбинаторики а) перестановки .б) размещения в) сочетания 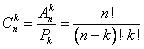 . 2. Классическое определение вероятности. , где - число благоприятствующих событию исходов, - число всех элементарных равновозможных исходов. . 2. Классическое определение вероятности. , где - число благоприятствующих событию исходов, - число всех элементарных равновозможных исходов.
3. Вероятность суммы событий Теорема сложения вероятностей несовместных событий:Теорема сложения вероятностей совместных событий:
4. Вероятность произведения событий. Теорема умножения вероятностей независимых событий:Теорема умножения вероятностей зависимых событий:, - условная вероятность события при условии, что произошло событие , - условная вероятность события при условии, что произошло событие . 5. Формула полной вероятности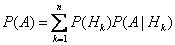 , где - полная группа гипотез, то есть , - достоверное событие. 6. Формула Байеса (формула Бейеса). Вычисление апостериорных вероятностей гипотез , где - полная группа гипотез, то есть , - достоверное событие. 6. Формула Байеса (формула Бейеса). Вычисление апостериорных вероятностей гипотез 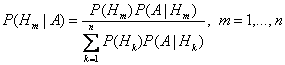 , где - полная группа гипотез. 7. Формула Бернулли , где - полная группа гипотез. 7. Формула Бернулли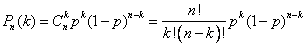 - вероятность появления события ровно раз при независимых испытаниях, - вероятность появления события при одном испытании. 8. Наивероятнейшее число наступления события. Наивероятнейшее число появления события при независимых испытаниях:, - вероятность появления события при одном испытании. - вероятность появления события ровно раз при независимых испытаниях, - вероятность появления события при одном испытании. 8. Наивероятнейшее число наступления события. Наивероятнейшее число появления события при независимых испытаниях:, - вероятность появления события при одном испытании.
Вопрос 42.
Теоремы сложения и умножения вероятностей.
Теоремы сложения и умножения вероятностей. Суммой двух событийА и В называется событие С, состоящее в появлении хотя бы одного из событий А или В. Теорема сложения вероятностей Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В). В случае, когда события А и В совместны, вер-ть их суммы выражается формулой Р (А +В) = Р (А) + Р (В) – Р (АВ), где АВ – произведение событий А и В.
Два события называются зависимыми, если вероятность одного из них зависит от наступления или не наступления другого. в случае зависимых событий вводится понятие условной вероятности события.
Условной вероятностью Р(А/В) события А называется вероятность события А, вычисленная при условии, что событие В произошло. Аналогично через Р(В/А) обозначается условная вероятность события В при условии, что событие А наступило.
Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В.
|
 Скачать 0.98 Mb.
Скачать 0.98 Mb.