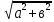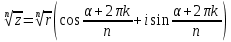43.Непрерывность функции на множестве
Говорят, что ф-я непрерывна на интервале, если она непрерывна в каждой точке этого интервала.
Говорят, что ф-я непрерывна на отрезке, если [a,b], если она непрерывна в каждой точке интервала (a,b), непрерывна слева в точке b и непрерывна справа в точке а.
Говорят, что ф-я непрерывна на полуинтервале [a,b), если она непрерывна в каждой точке интервала (а,b), и непрерывна справа в точке a.
Теорема о промежуточном значении. Если непрерывная на отрезке функция принимает значения разных знаков на концах отрезка, то она принимает на отрезке значение 0.
Теорема 2.6. непрерывная на отрезке функция принимает на этом отрезке все промежуточные значения. (Это значит, что если функция принимает на отрезке значения y1 и y2, то она принимает на этом отрезке и любое значение
y, расположенное между y1 и y2)
44. Сравнение и эквивалентность функции
Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→хо, т. е.
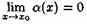 и и 
1. Если 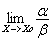 =А 0 (АєR), то α и ß называются бесконечно малыми одного порядка. =А 0 (АєR), то α и ß называются бесконечно малыми одного порядка.
2. Если, 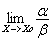 =0, то α називатся бесконечно малой более высокого порядка , чем ß. =0, то α називатся бесконечно малой более высокого порядка , чем ß.
3. Если 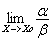 =∞, то α называется бесконечно малой более низкого порядка, чем ß. =∞, то α называется бесконечно малой более низкого порядка, чем ß.
4. Если 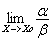 не существует, то α и ß называются несравнимыми бесконечно малыми. не существует, то α и ß называются несравнимыми бесконечно малыми.
Отметим, что таковы же правила сравнения б.м.ф. при х →±∞, х →х0±0.
2. Эквивалентные бесконечно малые и основные теоремы о них
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.
Если  то α и ß называются эквивалентными бесконечно малыми (при х→x0); это обозначается так: α то α и ß называются эквивалентными бесконечно малыми (при х→x0); это обозначается так: α
ß.
Например, sinx
х при х→0, т.к 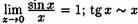 при x→0, т. к. при x→0, т. к. 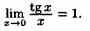
Теорема 18.1 . Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.

Теорема 18.2 . Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.
Действительно, так как
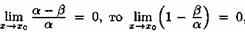 т. е. т. е.  Отсюда Отсюда 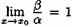 т. е. α т. е. α
ß. Аналогично, если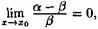 то α то α
ß.
Теорема 18.3 . Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Докажем теорему для двух функций. Пусть α→0, ß→0 при х→хо, причем α — б.м.ф. высшего порядка, чем ß, т. е.  . Тогда . Тогда
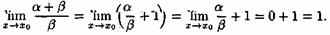
Следовательно, α+ß
ß при х→х0.
Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.
Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.
45.Алгебраическая форма записи комплексного числа. Действия над комплексными числами. Геометрическая интерпритация комплексного числа
Комплексное число – выражение вида z = a + bi, где a и b – действительные числа, i – число, кот. наз-ся мнимой единицей и явл. решением уравнения x2 + 1 = 0, т.е. i2 = −1.
Число a – действительная часть комплексного числа z и обозначается Rez, а число b – мнимой частью числа z и обозначается Imz.
Представление комплексного числа в виде z = a + ib называется алгебраической формой записи этого числа.
Плоскость, точки которой отождествляют с комплексными числами, называют комплексной плоскостью, ось абсцисс – действительной осью (на ней изображаются действительные числа), ось ординат – мнимой осью (на ней изображаются мнимые числа) комплексной плоскости.
46.Триганометрическая форма записи комплексного числа. Извлечение корней из комплексного числа
Запись комплексного числа в алгебраической форме z = a+bi соответствует на плоскости в прямоугольной системе координат Оху точка с абсциссой a и ординатой b. С каждой такой точкой связан радиус-вектор этой точки, длина которого равна r, r = |z| = 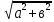
a = r cos α, b = r sin α.
Тогда комплексное число z = a + bi может быть записано в виде
z = r (cos α + i sin α) .
Представление комплексного числа в таком виде наз-ся тригонометрической формой записи комплексного числа.
Комплексное число z˜ наз-ся корнем n-й степени из комплексного числа z, если (z˜)n = z.
Теорема. Для каждого ненулевого комплексного числа z = r (cosα + isinα) существует в точности n значений корня n-й степени из z, которые могут быть определены по формуле
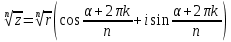 |
 Скачать 0.74 Mb.
Скачать 0.74 Mb.