шпоры. Шпора. 1. Матрицы. Определение и действия над ними. Матрицатаблица элементов любой природы. Под матрицей понимается
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Базисом в пространстве называется система трех линейно независимых векторов. Из определения базиса в пространстве и теоремы 17.6 следует, что любые три некомпланарных вектора являются базисом в пространстве. Координаты вектора- коэффициент разложение по базису. Любой вектор на прямой, на плоскости, в пространстве можно единственным образом разложить по векторам базиса на прямой, на плоскости, в пространстве. Теорема 17.9. Координаты суммы векторов a + b равны суммам соответствующих координат векторов a и b. Д о к а з а т е л ь с т в о. Пусть векторы a и b в базисе (e1, e2, e3) имеют координаты (α1, α2, α3) и (β1, β2, β3) соответственно. Тогда a = α1e1 + α2e2 + α3e3, b = β1e1 + β2e2 + β3e3. Следовательно, a + b = (α1 + β1)e1 + (α2 + β2)e2 + (α3 + β3)e3 и по определению координат вектора (α1 +β1, α2 +β2 α3 +β3) — координаты вектора a+b в базисе (e1,e2,e3). Теорема 17.10. Координаты произведения вектора a на число λ равны произведениям соответствующих координат вектора a на число λ. Д о к а з а т е л ь с т в о. Пусть вектор a в базисе (e1, e2, e3) имеет координаты (α1, α2, α3). Тогда a = α1e1 + α2e2 + α3e3. Следовательно,λa = λα1e1 + λα2e2 + λα3e3 и по определению координат вектора (λα1, λα2, λα3) — координаты вектора λa в базисе (e1, e2, e3). Следствие 17.10.1. Два ненулевых вектора a1(α1,α2,α3) и b(β1,β2,β3) коллинеарны тогда и только тогда, когда их координаты пропорциональны: 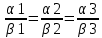 Декартовыми координатами вектора называются координаты вектора в базисе (i,j,k), состоящем из единичных векторов, сонаправленных с координатными осями Ox, Oy и Oz. Теорема 17.11. Декартовы координаты вектора X,Y,Z равны величинам проекций этого вектора на координатные оси Ox, Oy и Oz соответственно. Д о к а з а т е л ь с т в о. Пусть X,Y,Z — декартовы координаты некоторого вектора a. Отложим его от начала координат, и пусть a = OA. Построим точки A1, A2, A3 — проекции точки A на координатные оси. Тогда OA = OA1 +OA2 +OA3. Если (X,Y,Z) — декартовы координаты вектора a, то |a| = √X2 + Y 2 + Z2 Теорема 17.12. Пусть M1(x1,y1,z1) и M2(x2,y2,z2) — две произвольные точки. Тогда вектор −M−1−−M→2 имеет декартовы координаты (x2 − x1, y2 − y1, z2 − z1). Д о к а з а т е л ь с т в о. По определению суммы векторов OM2 = OM1 + −M1M2. Следовательно, M1M = OM2-OM1. Векторы OM2 и OM1 являются радиус-векторамиточек M2 и M1 и имеют координаты (x2, y2, z2) и (x1, y1, z1). Следовательно, вектор OM2 имеет координаты (x2 − x1, y2 − y1, z2 − z1). Направляющими косинусами вектора a называются числа cosα, cosβ, cosγ, где α,β,γ — углы между направлением вектора a и положительными направлениями координатных осей Ox, Oy и Oz соответственно. Теорема 17.13. Сумма квадратов направляющих косинусов вектора равна 1: cos2 α + cos2 β + cos2 γ = 1. 26.Координаты вектора, длина вектора. Направляющие косинусы вектора Координаты вектора- коэффициент разложение по базису. Любой вектор на прямой, на плоскости, в пространстве можно единственным образом разложить по векторам базиса на прямой, на плоскости, в пространстве. Теорема 17.9. Координаты суммы векторов a + b равны суммам соответствующих координат векторов a и b. Д о к а з а т е л ь с т в о. Пусть векторы a и b в базисе (e1, e2, e3) имеют координаты (α1, α2, α3) и (β1, β2, β3) соответственно. Тогда a = α1e1 + α2e2 + α3e3, b = β1e1 + β2e2 + β3e3. Следовательно, a + b = (α1 + β1)e1 + (α2 + β2)e2 + (α3 + β3)e3 и по определению координат вектора (α1 +β1, α2 +β2 α3 +β3) — координаты вектора a+b в базисе (e1,e2,e3). Теорема 17.10. Координаты произведения вектора a на число λ равны произведениям соответствующих координат вектора a на число λ. Д о к а з а т е л ь с т в о. Пусть вектор a в базисе (e1, e2, e3) имеет координаты (α1, α2, α3). Тогда a = α1e1 + α2e2 + α3e3. Следовательно,λa = λα1e1 + λα2e2 + λα3e3 и по определению координат вектора (λα1, λα2, λα3) — координаты вектора λa в базисе (e1, e2, e3). Следствие 17.10.1. Два ненулевых вектора a1(α1,α2,α3) и b(β1,β2,β3) коллинеарны тогда и только тогда, когда их координаты пропорциональны: 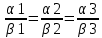 Длина вектора Следствие 17.11.2. Если (X,Y,Z) — декартовы координаты вектора a, то |a| = sqrt (X2 + Y 2 + Z2). Д о к а з а т е л ь с т в о. Отложим вектор a от начала координат и пусть a = OA. Тогда |a| = d(O,A). точка A будет иметь координаты (X, Y, Z). Тогда d(O,A) = sqrt ((X − 0)2 + (Y − 0)2 + (Z − 0)2 )= sqrt (X2 + Y 2 + Z2). Направляющими косинусами вектора a называются числа cosα, cosβ, cosγ, где α,β,γ — углы между направлением вектора a и положительными направлениями координатных осей Ox, Oy и Oz соответственно. Теорема 17.13. Сумма квадратов направляющих косинусов вектора равна 1: cos2 α + cos2 β + cos2 γ = 1. 27.Скалярное произведение векторов Скалярным произведением векторов a и b называется число (обозначается ab), равное произведению длин векторов на косинус угла между ними, то есть ab = |a||b| cos(a, b). Свойства скалярного произведения 1. ab = ba. 2. (αa)b = α(ab). Д о к а з а т е л ь с т в о. По следствию 17.1.1 прba = |a| cos(a, b). Следовательно, ab = |b|прba. Аналогично, (αa)b = |b|прb(αa). По теореме 17.2 прb(αa) = αпрb(a). Следовательно, (αa)b = |b|прb(αa) = |b|αпрb(a) = α(ab). 3. (a + b)c = ac + bc. Д о к а з а т е л ь с т в о. По следствию 17.1.1 прca = |a| cos(a, c). Следовательно, ac = |c|прca. Аналогично, bc = |c|прcb и (a + b)c = |c|прc(a + b). По теореме 17.3 прc(a + b) = прc(a) + прc(b). Следовательно, (a + b)c = |c|прc(a + b) = |c|прc(a) + |c|прc(b) = ac + bc. 4. Два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. Теорема 17.14. Пусть векторы a и b имеют декартовы координаты (X1,Y1,Z1) и (X2,Y2,Z2) соот- ветственно. Тогда скалярное произведение ab вычисляется по формуле: ab = X1X2 + Y1Y2 + Z1Z2. Д о к а з а т е л ь с т в о. Из определению декартовых координат вектора следует, что a = X1i + Y1j + Z1k, b = X2i + Y2j + Z2k, где i,j,k — единичные векторы, сонаправленные с осями Ox, Oy и Oz соответственно. Тогда по свойствам скалярного произведения ab = (X1i + Y1j + Z1k)(X2i + Y2j + Z2k) = (X1X2)ii + (X1Y2)ij + (X1Z2)ik+ (Y1X2)ji + (Y1Y2)jj + (Y1Z2)jk+ (Z1X2)ki + (Z1Y2)kj + (Z1Z2)kk. Так как векторы i,j,k попарно перпендикулярны, то их смешанные скалярные произведения равны нулю. Скалярные произведения этих же векторов на самих себя будут равны 1, так как их длины равны 1, а углы (i,^i),(j,^j), (k,^k) равны нулю. Следовательно, ab = X1X2 + Y1Y2 + Z1Z2. 28.Ориентация тройки векторов. Векторное произведение векторов Пусть (a,b,c) — упорядоченная тройка некомпланарных векторов. Отложим их от некоторой точки. Если, глядя с конца третьего вектора c, кратчайший поворот от первого вектора a ко второму вектору b осуществляется против часовой стрелки, то тройка векторов (a, b, c) называется правой, а если кратчайший поворот осуществляется по часовой стрелке, то левой. Из определения следует, что тройки векторов (a, b, c), (b, c, a), (c, a, b) являются тройками одной ориентации, а тройки (b, a, c), (a, c, b), (c, b, a) — тройки противоположной им ориентации. Заметим, что если декартова система координат в пространстве является правой, то упорядоченная тройка (i, j, k) направляющих векторов осей координат также является правой. Если же система координат левая, то тройка векторов (i, j, k) — левая. Векторным произведением вектора a на вектор b называется вектор (обозначается [a,b]), удовлетворяющий следующим условиям: 1) |[a, b]| = |a||b| sin(a,^b); 2) вектор [a, b] перпендикулярен каждому из векторов a и b. 3) упорядоченная тройка векторов (a, b, [a, b]) является правой. Свойства векторного произведения. 1. [a, b] = −[b, a]. 2. [αa, b] = α[a, b], [a, αb] = α[a, b]. 3. [a + b, c] = [a, c] + [b, c], [a, b + c] = [a, b] + [a, c]. 4. Ненулевые векторы a и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору Теорема 17.15. Пусть векторы a и b имеют декартовы координаты (X1,Y1,Z1) и (X2,Y2,Z2) соот- ветственно. Тогда координаты их векторного произведение [a,b] можно вычислить по формуле [a, b] = 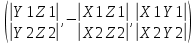 29.Смешанное произведение векторов Смешанным произведением упорядоченной тройки векторов (a,b,c) называется число (обозначается abc),равное скалярному произведению вектора c и векторного произведения [a, b], то есть abc = [a, b]c Свойства смешанного произведения. 1. Пусть V — объем параллелепипеда, построенного на отложенных от одной точки некомпланарных век- торах a, b, c. Тогда abc = 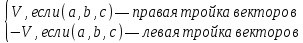 2. Векторы a, b, c компланарны тогда и только тогда, когда их смешанное произведение равно нулю. 3. abc = bca = cab = −acb = −cba = −bac. 4. (αa)bc = a(αb)c = ab(αc) = α(abc). 5. (a + d)bc = abc + dbc, a(b + d)c = abc + adc, ab(c + d) = abc + abd Теорема 17.16. Пусть векторы a,b,c имеют декартовы координаты (X1,Y1,Z1), (X2,Y2,Z2) и (X3,Y3,Z3) соответственно. Тогда их смешанное произведение abc можно вычислить по формуле abc = 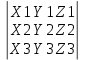 Д о к а з а т е л ь с т в о. По теореме вектор [b, c] имеет координаты [a, b] = 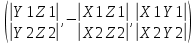 Следовательно, abc = a[b,c] = 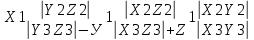 = = 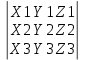 30.Уравнение плоскости Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору Ненулевой вектор перпендикулярный плоскости называется нормальным вектором этой плоскости. Теорема 18.10. Если плоскость проходит через точку M0(x0,y0,z0) и имеет нормальный вектор n(A,B,C) то ее уравнение имеет вид A(x − x0) + B(y − y0) + C(z − z0) = 0 Д о к а з а т е л ь с т в о. Произвольная точка M(x, y, z) будет лежать на плоскости тогда и только тогда, когда векторы M0M и n будут перпендикулярны. Но векторы M0M и n будут перпендикулярны тогда и только тогда, когда их скалярное произведение M0M·n будет равно нулю. Вектор M0M имеет координаты (x−x0,y −y0,z − z0). Следовательно, M0M · n = A(x − x0) + B(y − y0) + C(z − z0). Таким образом, точка M(x,y) будет лежать на прямой тогда и только тогда, когда выполняется равенство A(x − x0) + B(y − y0) + C(z − z0) = 0 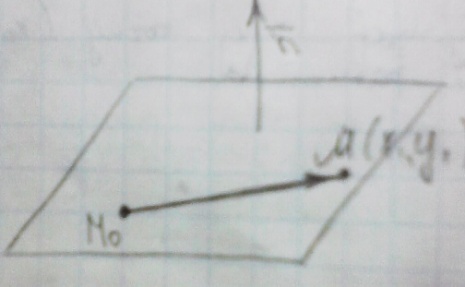 Общее уравнение плоскости Теорема 18.11. Любая плоскость в пространстве может быть задана уравнением вида Ax + By + Cz + D = 0 Если числа A, B и C не обращаются в ноль одновременно, то уравнение (18.3) является уравнением плоскости. Если два общих уравнения A1x + B1y + C1z + D1 = 0, A2x + B2y + C2z + D2 = 0 определяют одну плоскость, то A1/A2=B1/B2=C1/C2=D1/D2 Уравнение плоскости в отрезках Общее уравнение плоскости Ax+By+Cz+D = 0 называется полным, если все его коэффициенты не равны нулю, и неполным в противном случае. Неполные уравнения задают плоскости, которые проходят через начало координат, параллельны координатным осям и координатным плоскостям. Если общее уравнение Ax + By + Cz + D = 0 является полным, то его можно представить в виде 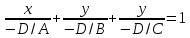 Обозначим a = −D/A, b = −D/B, c = -D/C Тогда уравнение плоскости примет вид 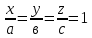 Нормальное уравнение плоскости Теорема 18.13. Уравнение xcosα + y cosβ + z cosγ − p = 0, является уравнением плоскости Π Уравнение плоскости, проходящей через три заданные точки Теорема 18.15. Если плоскость проходит через три различные точки M0(x0,y0,z0), M1(x1,y1,z1) и M2(x2,y2,z2), то ее уравнение имеет вид 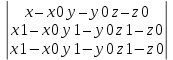 =0 =0Д о к а з а т е л ь с т в о. Произвольная точка пространства будет принадлежать рассматриваемой плоско- сти тогда и только тогда, когда векторы M0M, M0M1 и M0M2 будут компланарны. Но по свойствам смешанного произведения три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю. По теореме 17.16 смешанное произведение M0M M0M1 M0M2 имеет значение 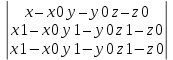 Приравняв его к нулю получим уравнение плоскости. Приравняв его к нулю получим уравнение плоскости.Взаимное расположение плоскостей Пусть в пространстве заданы плоскости Π1 и Π2: A1x + B1y + C1z + D1 = 0, Если плоскости Π1 и Π2 параллельны, то векторы n1 и n2 коллинеарны, и, следовательно, их координаты пропорциональны А1/В1=А2/В2=С1/С2 Это условие является и достаточным для параллельности плоскостей, если плоскости не совпадают угол ϕ между плоскостями Π1 и Π2 сводится к определению угла ϕ между векторами n1 и n2 cosϕ = 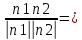 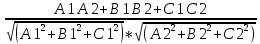 31,Уравнение прямой на плоскости Уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору Теорема 18.1. Если прямая проходит через точку M0(x0,y0) перпендикулярно ненулевому вектору n(A,B), то ее уравнение имеет вид A(x − x0) + B(y − y0) = 0 Д о к а з а т е л ь с т в о. Произвольная точка M(x, y) будет лежать на прямой тогда и только тогда, когда векторы M0M и n будут перпендикулярны. Но векторы M0M и n будут перпендикулярны тогда и только тогда, когда их скалярное произведение M0M · n будет равно нулю. Вектор M0M имеет координаты (x − x0,y − y0). Следовательно, M0M · n = A(x − x0) + B(y − y0). Таким образом, точка M(x,y) будет лежать на прямой тогда и только тогда, когда выполняется равенство A(x − x0) + B(y − y0) = 0 Общее уравнение прямой Теорема 18.2. Любая прямая на плоскости может быть задана уравнением вида Ax + By + C = 0. (18.1) Если числа A и B не обращаются в ноль одновременно, то уравнение (18.1) является уравнением прямой. Д о к а з а т е л ь с т в о. 1. Пусть ∆ — некоторая прямая на плоскости, M0(x0,y0) — точка на прямой, n(A,B) — ненулевой вектор, перпендикулярный ∆. Тогда по теореме 18.1 прямая может быть задана уравнением A(x − x0) + B(y − y0) = 0. Раскрыв скобки и обозначив через C число −Ax0 − By0 получим уравнение Ax + By + C = 0. 2. Рассмотрим уравнение Ax + By + C = 0. Так как коэффициенты A и B не обращаются в ноль од-новременно, то это уравнение всегда имеет решение (x0, y0) (например, в случае B =/ 0, выбрав произвольнозначение для x0, значение для y0 следует выбрать равным −1/B*(Ax0 + C)). Тогда Ax0 + By0 + C = 0. Вычитая это равенство из исходного уравнения, получаем уравнение A(x − x0) + B(y − y0) = 0, которое равносильноисходному уравнению и согласно теоремы 18.1 является уравнением прямой. Следовательно, и исходное уравнение Ax + By + C = 0 является уравнением прямой, причем по теореме 18.1 коэффициенты A и B являются координатами нормального вектора этой прямой. Общее уравнение прямой Ax + By + C = 0 называется полным, если все его коэффициенты не равны нулю,и неполным в противном случае. Уравнение прямой в отрезках Неполные уравнения задают прямые, проходящие через начало координат и параллельные координатным осям: 1. A = 0 — прямая параллельна оси Ox; 2. B = 0 — прямая параллельна оси Oy; 3. C = 0 — прямая проходит через начало координат; 4. A = 0, C = 0 — уравнение оси Ox; 5. B = 0, C = 0 — уравнение оси Oy. Если общее уравнение Ax + By + C = 0 является полным, то его можно представить в виде 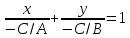 Обозначим a = −C/A, b = −C/B. Тогда уравнение прямой примет вид 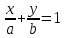 |
