шпоры. Шпора. 1. Матрицы. Определение и действия над ними. Матрицатаблица элементов любой природы. Под матрицей понимается
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Нормальное уравнение прямой Теорема 18.4. Уравнение xcosα + y sinα − p = 0, является нормальным уравнением прямой ∆. Д о к а з а т е л ь с т в о. Обозначим через P точку пересечения прямых ∆ и Γ, n — вектор, имеющий длину 1 и направление, совпадающее с направлением оси Γ. Заметим, что вектор n перпендикулярен прямой ∆. Произвольная точка M(x,y) будет принадлежать прямой ∆ тогда и только тогда, когда векторы n и PM будут перпендикулярны. Но тогда скалярное произведение n · P−−M→ должно быть равно нулю. По определению суммы векторов OP + PM = OM. Следовательно, PM = OM OP, и по свойствам скалярного произведения n·PM = n·OMn·OP. Так как вектор n имеет длину 1, то его декартовы координаты совпадают с направляющими косинусами: xn = cos α и yn = cos(α –π/2) = sinα. Вектор OM является радиус-вектором точки M. Следовательно, по следствию 17.11.1 его декартовы координаты совпадают с координатами точки M: xM = x, yM = y. Тогда по теореме 17.14 скалярное произведение n · OM имеет значение n · OM = xcosα + y sinα. Вычислим скалярное произведение n·O−−→P. Векторы n и O−−→P сонаправлены. Следовательно, угол между ними равен 0. Тогда n · OP = |n| · |OP|cos0 = |n| · |OP|. По построению |n| = 1, |OP| = p. Следовательно, n · OP = p. Таким образом, точка M(x, y) будет принадлежать прямой ∆ тогда и только тогда, когда ее координаты удовлетворяют уравнению xcosα + y sinα − p = 0 Параметрические уравнения прямой Теорема 18.6. Если прямая проходит через точку M0(x0,y0) и имеет направляющий вектор a(a1,a2), то уравнения 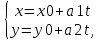 являются параметрическими уравнениями этой прямой. являются параметрическими уравнениями этой прямой.Каноническое уравнение прямой Теорема 18.7. Если прямая проходит через точку M0(x0,y0) и имеет направляющий вектор a(a1,a2), то ее уравнение имеет вид 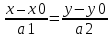 Уравнение прямой, проходящей через две заданные точки Пусть на плоскости задана декартова прямоугольная система координат Oxy. Если прямая ∆ проходит через две различные точки M0(x0,y0) и M1(x1,y1), то вектор −M−0−−M→1 является направляющим вектором этой прямой. Подставив координаты (x1 − x0, y1 − y0) этого вектора в каноническое уравнение прямой, получим уравнение прямой ∆ 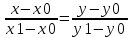 Уравнение прямой с угловым коэффициентом Углом наклона прямой к оси Ox называется угол, на который необходимо повернуть ось Ox против часовой стрелки, чтобы она стала параллельна прямой. Угловым коэффициентом прямой на плоскости называется тангенс угла наклона прямой к оси Ox. Теорема 18.8. Пусть ∆ — прямая, не параллельная оси Oy, k — ее угловой коэффициент. Тогда прямая может быть задана уравнением вида y = kx + b. –уравн с угл коэф Следствие 18.8.1. Пусть ∆ — прямая, не параллельная оси Oy, k — ее угловой коэффициент, M0(x0,y0) — точка на ∆. Тогда прямая может быть задана уравнением вида y = y0 + k(x − x0). Полярное уравнение прямой Теорема 18.9. Полярное уравнение r cos(ϕ − α) = p является уравнением прямой. 32. Уравнения прямой в пространстве Теорема 18.16. Если прямая проходит через точку M0(x0,y0,z0) и имеет направляющий вектор a(a1, a2, a3), то уравнение 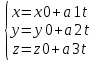 являются параметрическими уравнениями этой прямой. Д о к а з а т е л ь с т в о. Произвольная точка M(x, y, z) будет лежать на рассматриваемой прямой тогда и только тогда, когда векторы M0M и a будут коллинеарны. Коллинеарность векторов M0M и a равносильна рвенству M0M = ta, где t — некоторое число, которое может принимать любое значение от −∞ до +∞ в зависимости от длины вектора M0M. Так как вектор M0M имеет координаты (x − x0,y − y0,z − z0) а вектор ta координаты (ta1,ta2,ta3), то равенство M0M = ta равносильно системе 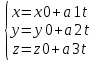 Канонические уравнение прямой Теорема 18.17. Если прямая проходит через точку M0(x0,y0,z0) и имеет направляющий вектор a(a1,a2,a3), то ее уравнения имеют вид 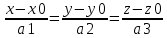 Уравнение прямой, проходящей через две заданные точки Если прямая ∆ проходит через две различные точки M0(x0,y0,z0) и M1(x1,y1,z1), то вектор M0M1 яв-ляется направляющим вектором этой прямой. Подставив координаты (x1 − x0,y1 − y0,z − z0) этого вектора в каноническое уравнение прямой, получим уравнение прямой ∆ 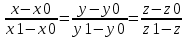 33. Эллипс и его каноническое уравнение Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (обозначается 2a) и большая, чем расстояние между фокусами (обозначается 2c). Теорема 19.2. Эллипс, фокусы которого лежат на оси Ox и равноудалены от оси Oy, задается уравнением  где b =sqrt (a2 − c2) 34. Гиперболa и ее каноническое уравнение Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (обозначается 2a), не равная нулю и меньшая, чем расстояние между фокусами (обозначается 2c). Теорема 19.3. Гипербола, фокусы которой лежат на оси Ox и равноудалены от оси Oy, задается уравнением 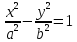 где b =sqrt (c2- a2 ) 35.Парабола и ее каноническое уравнение Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом,и данной прямой, называемой директрисой. Расстояние от фокуса параболы до директрисы называется параметром параболы и обозначается p. Теорема 19.5. Парабола, фокус которой лежит на оси Ox, директриса параллельна оси Oy, начало координат равноудалено от фокуса и директрисы, задается уравнением y2 = 2px, где p — параметр параболы. 36. Числовая последовательность. Бесконечно малые последовательности Последовательностью действительных чисел называют отображение упорядоченного естественным образом (по возрастанию) множества N в множество R, при котором каждому n ∈ N ставится в соответствие число an. Числа an называют членами (элементами) последовательности Удалим из последовательности (an) какие-либо элементы так, что останется бесконечное множество элементов. Оставшиеся элементы не переставляем местами. Они образуют последовательность, называемую подпоследовательностью последовательности (an). Ограниченная последовательность Последовательность (an) называют ограниченной, если ограничено множество {an} всех элементов этой последовательности. Теорема 1.1. Если последовательность ограничена, то ограничен и любой ее остаток. Если какой-либо остаток последовательности ограничен, то и сама последовательность ограничена. Последовательность (αn) называют бесконечно малой последовательностью, если ∀ ε > 0 ∃ν = νε > 0 такое, что ∀n>= ν ⇒ |αn| <= ε. Свойства бесконечно малых последовательностей: Свойство 1. Бесконечно малая последовательность ограничена. Свойство 2. Сумма двух бесконечно малых последовательностей является бесконечно малой последовательностью. Свойство 3. Сумма любого фиксированного числа бесконечно малых последовательностей является бесконечно малой последовательностью. Свойство 4. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью Свойство 5. Произведение двух бесконечно малых последовательностей является бесконечно малой последовательностью Свойство 6. Произведение любого фиксированного числа бесконечно малых последовательностей является бесконечно малой последовательностью. Свойство 7. Если все элементы бесконечно малой последовательности равны, то они равны нулю. 37.Сходящиеся последовательности Последовательность (an) называют сходящейся, если существует такое число a, что ∀ε > 0 ∃ν = νε > 0 такое, что ∀ n ۀ ν ⇒ |an − a| ﻠ ε. Последнее неравенство равносильно тому, что a − ε ≤ an ≤ a + ε. При этом используют обозначение an → a или lim n→∞ an = a. Свойства сходящихся последовательностей Свойство 1. Сходящаяся последовательность имеет только один предел. Свойство 2. Сходящаяся последовательность ограничена. Свойство 3. Если an → a и bn → b, то Aan + Bbn → Aa + Bb. Свойство 4. Если an → a и bn → b, то an · bn → a · b. Свойство 5. Если an → a, bn → b, и bn =/ 0 при любом n, b =/ 0, то аn/bn →a/b Свойство 6. Если an → a, bn → b и an <= bn, при любом n, то a <= b. Теорема 1.2 (о сжатой последовательности). Если последовательности (an) и (bn) имеют общий предел h и an <=cn <= bn при любом n, то и последовательность (cn) сходится к h. 38. Монотонные последовательности Последовательность (an) называют возрастающей, если она удовлетворяет условию : an+1 >= an при любом n. Последовательность (an) называют строго возрастающей, если она удовлетворяет условию : an+1 > an при любом n. Последовательность (an) называют убывающей, если она удовлетворяет условию : an+1 <= an при любом n. Последовательность (an) называют строго убывающей, если она удовлетворяет условию : an+1 < an при любом n. Убывающую и возрастающую последовательности называют монотонными. Строго убывающую и строго возрастающую последовательности называют строго монотонными. Последовательность называют монотонной в широком смысле, если она имеет монотонный остаток. Теорема 1.4 (Критерий сходимости монотонной последовательности). Всякая монотонная ограниченная последовательность сходится. Число e. Последовательность an = (1 +1/n)n возрастает и ограничена сверху числом 3. Поэтому она сходится. Ее предел обозначают e. Это иррациональное число, e = 2, 71828... Таким образом lim(1 +1/n)n = e n→∞ 39.Понятие функции. Первый и второй замечательный пределы Функцией, определенной на множестве X со значениями в множестве Y называют закон f, по которому каждому элементу x ∈ X ставится в соответствие элемент y ∈ Y. Элемент y называют образом элемента x и обозначают y = f(x). При этом записывают f : X → Y или, более подробно, f : x → y = f(x). Множество X называют областью определения функции. В этом разделе мы будем рассматривать числовые функции y = f(x) с числовыми значениями, т.е. считать, что X и Y - множества из R. При этом x называют независимой переменной или аргументом функции, а y -зависимой переменной. Окрестностью точки a называют всякий интервал Ua = (α, β,) содержащий точку a. Точку a ∈ R называют предельной точкой множества X, если X ∩U˙a =/ ∅ для любой проколотой окрестности U˙a точки a Пусть функция f определена на множестве X и a - предельная точка множества X. Число A называют пределом функции в точке a, если ∀ε > 0 ∃δε, ∀x ∈ X, 0 < |x − a| Б= δε ⇒ |f(x) − A|<= ε. При этом используют обозначения lim= A x→a или f(x) → A при x → a Теорема 2.1. Пусть функция y = f(x) определена на множестве X и a - предельная точка множества X. Предел функции в точке a существует и равен A тогда и только тогда, когда для любой последовательности (xn) со свойствами: xn → a, xn ∈ X при любом n, xn ʰ= a соответствующая последовательность значений функции (yn) = (f(xn)) имеет предел A. 40. Предел функции Число L называется пределом функции y = f ( x ) при x, стремящемся к a : если для любого Это определение означает, что L есть предел функции y = f ( x ), если значение функции неограниченно приближается к L , когда значение аргумента xприближается к a. Геометрически это значит, что для любого    41. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ. ТОЧКТ РАЗРЫВА Пусть функция f(x) определена на интервале Х и х0 ∈ Х 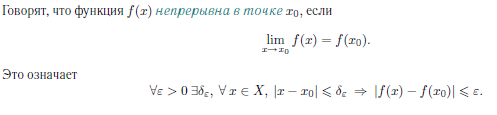 Необходимое и достаточное условие непрерывности функции в точке Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда Замечание. Условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.       42.ТОЧКИ РАЗРЫВА ФУНКЦИИ. ИХ КЛАССИФИКАЦИЯ      |
