шпоры. Шпора. 1. Матрицы. Определение и действия над ними. Матрицатаблица элементов любой природы. Под матрицей понимается

• Название: 1. Матрицы. Определение и действия над ними. Матрицатаблица элементов любой природы. Под матрицей понимается
• Анкор: шпоры
• Дата: 26.09.2022
• Размер: 0.74 Mb.
• Имя файла: Шпора.docx
• Тип: Документы; #697772
• страница: 2 из 5

Часть прямой, ограниченная двумя точками, называется отрезком.

Длиной отрезка d(A, B) называют число, полученное измерением этого отрезка с помощью некоторого отрезка, принятого за единицу длины.

Отрезок называется направленным, если указано, какая из его граничных точек является началом, а какая концом. обозначается AB.

Направленный отрезок называется нулевым, если его начальная и конечная точка совпадают. Нулевой отрезок не имеет определенного направления.

Прямая с указанным направлением называется осью.

Величиной направленного отрезка AB на оси ∆ называется число, равное длине отрезка, взятой знаком плюс, если его направление совпадает с направлением оси, и со знаком минус, если направления оси и отрезка противоположны, то есть

d(A,B), если AB ↑↑ ∆

−d(A,B), если AB ↑↓ ∆

Декартовой координатой x_M произвольной точки M на координатной оси называется величина направленного отрезка OM, то есть x_M = OM.

Пусть M₁(x₁) и M₂(x₂), две точки расположенные на координатной оси. Тогда величина направленного отрезка M₁M₂ равна разности декартовых координат конечной и начальной точек, то есть

M₁M₂ = x₂ − x₁

Расстояние d(M₁,M₂) между точками M₁(x₁) и M₂(x₂) на координатной оси вычисляется по формуле

d(M₁,M₂) = |x₂ − x₁|
Пусть M1 и M2, две различные точки расположенные на оси. Говорят, что точка M делит направленный отрезок M1M2 в отношении λ, если

λ =M1M/MM2

где M1M и MM2 — величины направленных отрезков M1M и MM2. Если точка M лежит между точками M1 и M2, то говорят, что она делит отрезок M1M2 внутренним образом, если же точка M расположена вне

отрезка M1M2, то говорят, что она делит отрезок внешним образом. Число λ при этом называют простым отношением трех точек M1, M и M2.

Свойства простого отношения трех точек.

1. Простое отношение трех точек не может принимать значение -1.

Д о к а з а т е л ь с т в о. Если λ = −1, то M1M/MM2= −1 ⇒ M1M = −MM2 ⇒ M1M = M2M, что возможно лишь в случае совпадения точек M1 и M2, а это противоречит исходному требованию различияэтих точек.

2. Если точка M делит направленный отрезок M1M2 в отношении λ, то отрезок M2M1 точка M делит в отношении 1/λ

Д о к а з а т е л ь с т в о. Если M1M/MM2= λ, то M2M/MM1= −MM2/−M1M=MM2/M1M=1/λ

3. Простое отношение трех точек M1, M и M2 принимает положительное значение, если точка M делит направленный отрезок M1M2 внутренним образом, и отрицательное значение, если точка M делит направленный отрезок M1M2 внешним образом.
18.Декартовы координаты на плоскости
Декартову прямоугольную систему координат на плоскости образуют две перпендикулярные координатные оси с общим началом координат и одинаковой единицей масштаба. Одну из осей называют осью абсцисс или осью Ox, другую осью ординат или осью Oy.

Если кратчайший поворот от первой оси ко второй осуществляется против часовой стрелки, то система координат называется правой, если по часовой стрелке, то левой.

Пусть M — произвольная точка плоскости, на которой задана декартова прямоугольная система координат,Mx и My — проекции точки M на координатные оси Ox и Oy соответственно. Декартовыми прямоугольными координатами x и y точки M (обозначается M(x,y)) называются числа, равные величинам направленных отрезков OMx и OMy на осях Ox и Oy соответственно, то есть

x = OMx, y = OMy.

Расстояние d(M1,M2) между двумя произвольными точками плоскости M1(x1,y1) и M2(x2,y2) вычисляется по формуле

d(M1,M2) = (

Если точка M(x,y) делит направленный отрезок M1M2, ограниченный точками M1(x1,y1) и M2(x2,y2), в отношении λ то ее координаты равны

x =x1 + λx2/1 + λ

y =y1 + λy2/1 + λ
19.Декартовы координаты в пространстве



Декартову прямоугольную систему координат в пространстве образуют три взаимно перпендикулярные координатные оси с общим началом координат и одинаковой единицей масштаба. Одну из осей называют осью абсцисс или осью Ox, другую осью ординат или осью Oy, третью осью аппликат или осью Oz.

Система координат называется правой, если глядя со стороны положительной полуоси Oz кратчайший поворот от оси Ox к оси Oy осуществляется против часовой стрелки, и левой, если по часовой стрелке.

Пусть в пространстве задана декартова прямоугольная система координат, M — произвольная точка пространства, Mx, My и Mz — ее проекции на координатные оси Ox, Oy и Oz соответственно. Декартовыми прямоугольными координатами x, y, z точки M (обозначается M(x,y,z)) называются числа, равные величинам направленных отрезков OMx, OMy и OMz на на осях Ox, Oy и Oz соответственно, то есть

x = OMx, y = OMy, y = OMz

Расстояние d(M1,M2) между двумя произвольными точками плоскости M1(x1,y1,z1) и M2(x2,y2,z2) вычисляется по формуле

d(M1,M2) = sqrt ( (x2 − x1)^2 + (y2 − y1)^2 + (z2 − z1)^2 )

20. Полярные координаты на плоскости
Полярную систему координат на плоскости образуют точка O, выходящий из нее луч Ox и единица масштаба для измерения длин. При этом точка O называется полюсом, луч Ox — полярной осью.

Пусть на плоскости задана полярная система координат и пусть M — произвольная точка плоскости. Полярными координатами точки M называются два числа r и ϕ, первое из которых равно расстоянию от точки M до полюса, второе — угол, на который необходимо полярную ось против часовой стрелки вокруг полюса O до совмещения ее с лучом OM. При этом первая координата r называется полярным радиусом точки M, вторая координата ϕ — полярным углом.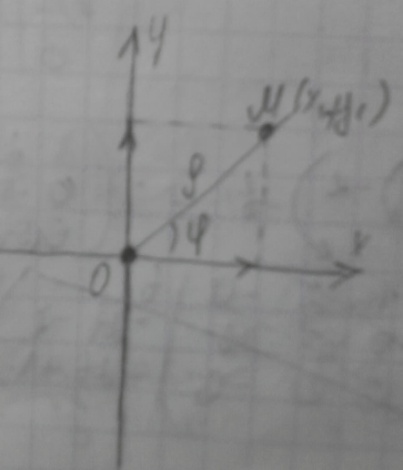



Связь между полярными и декартовыми координатами точки

Расположим декартову прямоугольную систему координат и полярную систему координат таким образом, чтобы полюс совпадал с началом декартовой системы координат, а полярная ось с положительной полуосью Ox. Пусть M произвольная точка плоскости, (x,y) — ее декартовы координаты, (r,ϕ) — полярные координаты .

Тогда

x = r cos ϕ, y = r sin ϕ.

Полярные координаты точки выражаются через декартовы формулами

r = sqrt (x^2 + y^2)

cosϕ = x/ sqrt(x^2 + y^2)

sin ϕ =y/sqrt (x^2 + y^2)
21. Уравнение линии на плоскости. Уравнение линии и поверхности в пространстве
Уравнением линии L в заданной системе координат называют уравнение вида

F(x, y) = 0, (16.1)

которому удовлетворяют координаты всех точек, лежащих на линии, и только они.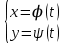



называют параметрическими уравнениями линии, а переменная t — параметром

Уравнение поверхности в пространстве

Уравнением поверхности S в заданной системе координат называют уравнение вида

F(x, y, z) = 0,

которому удовлетворяют координаты всех точек, лежащих на поверхности, и только они. При этом говорят, что уравнение определяет поверхность S.

Уравнение линии в пространстве

Любую линию в пространстве можно рассматривать как линию пересечения поверхностей. Если F1(x,y,z) = 0 и F2(x, y, z) = 0 — уравнения этих поверхностей, то координаты точек линии пересечения должны удовлетворять каждому из этих уравнений. Следовательно, уравнения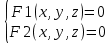


совместно определяют линию, то есть являются уравнениями этой линии.

Параметрическое уравнение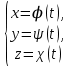

22. Понятие вектора. Линейные операции над векторами
Вектор с началом в точке A и концом в точке B обозначают AB. Длину вектора AB обозначают |AB|. Заметим, что |AB| = d(A,B)

Нулевой вектор не имеет определенного направления и имеет длину равную нулю.

Вектор, длина которого равна 1, называется единичным.

Вектор b, называется противоположным вектору a (обозначается −a), если его длина равна длине вектора, а направление противоположно направлению вектора a.

Два вектора называются равными, если их длины равны, а направления совпадают.

Направленные векторы равной длины азываются свободными векторами. Свободный вектор допускает перенос в любую точку при условии сохранения длины и направления вектора.

Откладыванием вектора a от точки O называется построение вектора, имеющего начало в точке O и равного вектору a.

Пусть a и b — два произвольных ненулевых вектора. Отложим их от некоторой точки O, и пусть a = OA, b=OB. Угол при вершине O в треугольнике OAB называется углом между векторами a и b и обозначается (a,^b). 0 <=(a,^b) <=π

Линейные операции над векторами

1. Произведением вектора a на действительное число α называется вектор (обозначается αa) длина ко-

торого равна длине вектора a, умноженной на |α|, а направление совпадает с направлением вектора a, если

α > 0, и противоположно направлению вектора a, если α < 0.

2. Суммой двух векторов a и b называется вектор (обозначается a+b), который строится по правилу треугольника или параллелограмма. Для этого необходимо отложить вектор b от конца вектора a. Тогда вектор, начало которого совпадает с началом вектора a, а конец с концом вектора b (и любой равный ему) и является суммой a + b.

3. Разностью векторов a и b называется вектор (обозначаем a − b), который при сложении с вектором b дает

вектор a, то есть такой, что b + (a − b) = a.

Свойства линейных операций.

1. a + b = b + a (коммутативность сложения).

2. (a + b) + c = a + (b + c) (ассоциативность сложения).

3. a + 0 = a.

4. a + (−a) = 0.

5. (αβ)a = α(βa).

6. (α + β)a = αa + βa.

7. α(a + b) = αa + αb.

8. 1 · a = a, (−1) · a = −a, 0 · a = 0.
23. Коллинеарные и компланарные векторы. Проекция вектора на ось
Векторы называются коллинеарными, если они расположены либо на одной прямой, либо на параллельных.(векторное произведение =0).

Коллинеарные векторы либо одинаково направлены, либо направлены противоположно. Единичные коллинеарные векторы или равны, или противоположны.

Лемма. Два ненулевых вектора a1 и a2 коллинеарны тогда и только тогда, когда существует число λ, такое что a1 = λa2.

Векторы называются компланарными, если они расположены либо на одной плоскости, либо на параллельных. (смешанное произведение =0)

Пусть a — произвольный вектор, ∆ — некоторая ось. Отложим вектор a от некоторой точки A, и пусть a=AB. Построим проекции A1 и B1 точек A и B на ось ∆. Вектор A1B1 называется проекцией вектора a на ось∆.

Пусть a — произвольный вектор, ∆ — некоторая ось, A−−1−B→1 — проекция вектора a на ось ∆. Величиной проекции вектора a на ось ∆ (обозначается пр∆a) будем называть величину направленного отрезка A1B1 на оси ∆

Величиной проекции вектора a на вектор b (обозначается прba) будем называть величину проекции вектора a, на любую ось, сонаправленную с вектором b.

Теорема. Величина проекции вектора a на ось ∆ равна

пр_∆a = |a|cos(a,^∆),

где (a,^∆) — угол между направлением вектора a и положительным направлением оси ∆.

(a,ꈐ∆) — угол между направлением вектора a и положительным направлением оси ∆.

Д о к а з а т е л ь с т в о. Обозначим через O — произвольную точку на оси ∆ и отложим от нее вектор a.

1. Если угол ϕ между направлением вектора a и положительным направлением оси ∆ острый, то направление отрезка OA1 совпадает с направлением оси. Следовательно,

пр∆a = |OA1| = |OA|cosϕ = |a|cosϕ.

2. Если угол ϕ между направлением вектора a и положительным направлением оси ∆ тупой (рис.), то направление отрезка OA1 противоположно направлению оси. Следовательно,

пр∆a = −|O−−A→1| = −|O−→A|cos(π − ϕ) = |a|cosϕ

Следствие. Величина проекции вектора a на вектор b равна

прba = |a|cos(a,^b)

Теорема . пр_∆(αa) = αпр_∆a.

Д о к а з а т е л ь с т в о. По теореме пр∆αa = |αa|cos(αa^,∆) = |α||a|cos(αa^,∆).

Если α > 0, то |α| = α и (αa^,∆) = (a,^∆). Следовательно,

пр∆αa = α|a|cos(a,^∆) = αпр∆a.

Если α < 0, то |α| = −α и (αa^,∆) = π − (a,^∆). Следовательно,

пр∆αa = −α|a|cos(π − (a,^∆)) = α|a|cos(a,^∆) = αпр∆a.
Теорема . пр_∆(a + b) = пр_∆a + пр_∆b.

Д о к а з а т е л ь с т в о. Пусть a = AB, b = BC. Тогда a+b = AC. Построим точки A1, B1, C1 — проекции

точек A, B, C на ось ∆ (рис). Тогда

пр∆a = A1B1, пр∆b = B1C1, пр∆(a + b) = A1C1.

A1B1 + B1C1 = A1C1. Следовательно,

пр∆a + пр∆b = пр∆(a + b).
24. Линейная зависимость и независимость векторов
Линейной комбинацией векторов a1, a2, . . . , an называется вектор вида

α1a1 + α2a2 + ··· + αnan,

где α1, α2, . . . , αn — произвольные действительные числа.

Если некоторый вектор b представлен в виде линейной комбинации векторов a1, a2, . . . , an, то говорят, что он разложен по этим векторам.

Система векторов a1,a2,...,an называется линейно зависимой, если существую не обращающиеся одновременно в ноль действительные числа α1, α2, . . . , αn, такие что линейная комбинация α1a1+α2a2+···+αnan равна нулевому вектору, и независимой, если нулевому вектору равна лишь линейная комбинация с нулевыми коэффициентами.

Теорема 17.4. Если система векторов a1,a2,...,an содержит нулевой вектор, то она линейно зависима.

Д о к а з а т е л ь с т в о. Пусть один из векторов системы a1, a2, . . . , an, например вектор a1, является нулевым. Тогда линейная комбинация

1 · a1 + 0 · a2 + · · · + 0 · an

имеет среди коэффициентов ненулевые и равна нулевому вектору.

Теорема 17.5. Два ненулевых вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Д о к а з а т е л ь с т в о. Необходимость. Если ненулевые векторы a1 и a2 линейно зависимы, то существует равная нулевому вектору линейная комбинация α1a1+α2a2 c не обращающимися одновременно в ноль коэффициентами. Без ограничения общности будем считать, что α1 =/ 0. Тогда a1 = −α2/α1 *a2. Следовательно, по лемме векторы a1 и a2 коллинеарны.

Достаточность. Пусть ненулевые векторы a1 и a2 коллинеарны. Тогда по лемме 17.1 существует число λ,

такое что a1 = λa2. Следовательно, a1−λa2 = 0, то есть a1−λa2 — линейная комбинация c не обращающимися одновременно в ноль коэффициентами и равная нулевому вектору.

Теорема 17.6. Три ненулевых вектора линейно зависимы тогда и только тогда, когда они компланарны.

Д о к а з а т е л ь с т в о. Необходимость. Если ненулевые векторы a1, a2 и a3 линейно зависимы, то существует равная нулевому вектору линейная комбинация α1a1 + α2a2 + α3a3 c не обращающимися одновременно в ноль коэффициентами. Без ограничения общности будем считать, что α1 =/ 0. Тогда

a1=-α2/α1 *a2 −α3/α1 *a3.

Следовательно, вектор a1 будет параллелен той же плоскости, что и векторы a2 и a3.

Достаточность. Пусть ненулевые векторы a1, a2 и a3 компланарны. Отложим их от некоторой точки O и

пусть a1 = OA1, a2 = OA2, a3 = OA3. Через точку A3 проведем прямые, параллельные векторам OA1 и OA2. Обозначим через M1 и M2 точки пересечения этих прямых с прямыми OA1 и AO2. По определению суммы векторов a3 = OM1 + OM2.

Векторы OA1 и OM1 коллинеарны. Следовательно, по лемме 17.1 существует число λ1, такое что OM1=λ1OA1. Векторы OA2 и OM2 также коллинеарны и следовательно, существует число λ2, такое что OM2=λ1OA2. Тогдаa3 = λ1OA1 + λ2OA2 = λ1a1 + λ2a2,

Следовательно, a3 − λ1a1 − λ2a2 = 0, то есть a3 − λ1a1 − λ2a2 — линейная комбинация c не обращающимися одновременно в ноль коэффициентами и равная нулевому вектору.

Теорема 17.7. Система векторов, состоящая из четырех или более ненулевых векторов, линейно зависима.
25. Базис на прямой, на плоскости, в пространстве. Координаты вектора. Направляющие косинусы вектора
Базисом на прямой называется линейно независимая система векторов, состоящая из одного вектора, параллельного этой прямой.

Из теоремы 17.4 следует, что базис не может содержать нулевой вектор. Следовательно, любой ненулевой вектор параллельный прямой является базисом на этой прямой.

Базисом на плоскости называется линейно независимая система векторов, состоящая из двух векторов, параллельных этой плоскости.

Из определения базиса на плоскости и теоремы 17.5 следует, что любые два неколлинеарных вектора параллельных плоскости являются базисом на этой плоскости.