Определение модуля непрерывности функции на множестве. Примеры нахождения модуля непрерывности
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
Определение модуля непрерывности функции на множестве. Примеры нахождения модуля непрерывности. Xác định môđun liên tục của một hàm trên một tập hợp. Ví dụ về việc tìm môđun của tính liên tục.  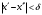 свойста: он всегда неотрицательный, представляет собой неубывающую функцию δ всюду на полупрямой δ>0. При уменьшении δ множество, по которому берётся супремум, сужается, а супремум на части множества не превосходит супремума на всём множестве. свойста: он всегда неотрицательный, представляет собой неубывающую функцию δ всюду на полупрямой δ>0. При уменьшении δ множество, по которому берётся супремум, сужается, а супремум на части множества не превосходит супремума на всём множестве.tính chất: nó luôn luôn không âm, là một hàm không giảm của δ ở mọi nơi trên nửa đường δ> 0. Khi δ giảm, tập hợp mà giá trị tối cao được lấy sẽ thu hẹp lại và giá trị tối cao trên một phần của tập hợp không vượt quá giá trị tối cao trên toàn bộ tập hợp. Эквивалентные определения равномерной непрерывности функции на множестве. Сравнение непрерывности и равномерной непрерывности. Các định nghĩa tương đương về tính liên tục đồng nhất của một hàm số trên một tập hợp. So sánh tính liên tục và tính liên tục đồng đều. Определение 1:  называется равномерно непрерывной на множестве А : được gọi là liên tục đồng nhất trên tập A,, называется равномерно непрерывной на множестве А : được gọi là liên tục đồng nhất trên tập A,,  (  , , 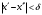 ) ) Определение 2(Критерий Коши):  - равномерно непрерывная функция на множестве - равномерно непрерывная функция на множестве Định nghĩa 2 (Tiêu chuẩn Cauchy): - Hàm số liên tục đồng biến trên tập A, nếu tại x , если  при х’, x” принадлеж. А при х’, x” принадлеж. АТеорема 1 (Эквивалентность определений 1 и 2) Доказательство: Так как 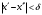 и и  выполняется Критерий Коши. выполняется Критерий Коши. Теорема о равномерной непрерывности функции, непрерывной на отрезке. Định lý về tính liên tục đồng đều của hàm số liên tục trên một khoảng. Если функция определе теорему об общем виде первообразных на и непрерывна на отрезке, то она равномерно непрерывна на нем (для интервала не работает) Nếu một hàm được xác định và liên tục trên một đoạn thì nó là liên tục đồng nhất trên nó (không hoạt động trong một khoảng thời gian) (). (  ). ). Доказательство: Допустим что теорема неверна. Тогда существует ε>0 Giả sử định lý là sai. Khi đó tồn tại ε> 0  (: найдётся пара точек x’, x” có một cặp điểm x ', x ”) Зададим стремящуюся к 0 последовательность положительных чисел Hãy xác định một dãy số dương có xu hướng là 0, khi đó (: найдётся пара точек x’, x” có một cặp điểm x ', x ”) Зададим стремящуюся к 0 последовательность положительных чисел Hãy xác định một dãy số dương có xu hướng là 0, khi đó  , тогда , тогда  . Так как точки последовательности Kể từ khi các điểm của chuỗi . Так как точки последовательности Kể từ khi các điểm của chuỗi 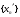 принадлежат к отрезку thuộc về phân khúc принадлежат к отрезку thuộc về phân khúc , то эта последовательность ограничена, и из нее можно выделить, по теореме Больцано-Вейерштрасса, подпоследовательность thì dãy này bị giới hạn, và từ đó, theo định lý Bolzano-Weierstrass, một dãy con có thể được phân biệt, , то эта последовательность ограничена, и из нее можно выделить, по теореме Больцано-Вейерштрасса, подпоследовательность thì dãy này bị giới hạn, và từ đó, theo định lý Bolzano-Weierstrass, một dãy con có thể được phân biệt, , сходящуюся к некоторой точке , сходящуюся к некоторой точке hội tụ đến một điểm nào đó  . Значит, из нее можно выделить также подпоследовательность Do đó, một dãy con cũng có thể được phân biệt với nó. . Значит, из нее можно выделить также подпоследовательность Do đó, một dãy con cũng có thể được phân biệt với nó.  . Аналогично выделим подпоследовательность Tương tự, hãy chọn một dãy con . Аналогично выделим подпоследовательность Tương tự, hãy chọn một dãy con  и и   . Получили противоречие – теорема доказана. (f(x’nk) стр.к f(x0), f(x”nk) стр.к f(x0),а их разность не стремится-противоречие) . Получили противоречие – теорема доказана. (f(x’nk) стр.к f(x0), f(x”nk) стр.к f(x0),а их разность не стремится-противоречие) Chúng ta có một mâu thuẫn - định lý được chứng minh. (f (x'nk) dòng thành f (x0), f (x "nk) dòng đến f (x0) và sự khác biệt của chúng không có xu hướng - mâu thuẫn) Необходимость условия: Điều kiện cần thiết:  , то теорема 2 не выполняется. , то теорема 2 не выполняется. thì Định lý 2 là sai. Пример  Пусть Пусть  при при  . .Производная. Определение, непрерывность функции, имеющей производную. Геометрический смысл производной. Необходимое условие существования производной. Phát sinh. Định nghĩa, tính liên tục của một hàm số có đạo hàm. Ý nghĩa hình học của đạo hàm. Một điều kiện cần thiết để tồn tại một đạo hàm. Определение: Производной от функции  в точке в точке  называется предел, к которому стремится отношение ее приращения называется предел, к которому стремится отношение ее приращения 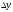 в этой точке к соответствующему приращению в этой точке к соответствующему приращению  аргумента, когда последнее стремится к нулю: аргумента, когда последнее стремится к нулю:Định nghĩa: Đạo hàm của một hàm tại một điểm là giới hạn mà tỷ số giữa số gia của nó tại điểm đó với số gia tương ứng của đối số có xu hướng khi giá trị sau có xu hướng bằng không: 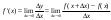 Т.е., если  определена в определена в 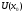 , то , то   Теорема: (необходимое условие существования производной) Định lý: (điều kiện cần để tồn tại đạo hàm) Для существования производной от f в точке x необходимо, чтобы функция f была определена в некоторой окрестности точки х, в том числе в самой точке х. Но не для всякой функции f, определенной в окрестности точки х, существует предел. Обычно, когда говорят, что функция f имеет в точке х производную, подразумевают, что она конечная т.е. предел конечный. Если предел бесконечный, то f имеет бесконечную производную.(y=|x|) Để tồn tại đạo hàm của f tại điểm x, thì hàm f phải được xác định trong một lân cận nào đó của điểm x, bao gồm tại chính điểm x. Nhưng không phải mọi hàm f xác định trong một lân cận của điểm x đều có giới hạn. Thông thường, khi họ nói rằng hàm f có đạo hàm tại điểm x, họ có nghĩa là nó hữu hạn, tức là giới hạn cuối. Nếu giới hạn là vô hạn thì f có đạo hàm vô hạn. (Y = | x |) Если функция  имеет конечную имеет конечную  в точке в точке  , то , то  непрерывна в точке непрерывна в точке  . .Nếu hàm hữu hạn tại điểm, thì nó liên tục tại điểm Доказательство: 1=   Предел 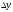 при при  =0 =0Следовательно  - непрерывна в точке - непрерывна в точке  . Do đó - là liên tục tại điểm. . Do đó - là liên tục tại điểm.Теорема доказана. Định lý đã được chứng minh. Замечание: обратное утверждение неверно, если функция  непрерывна в точке непрерывна в точке  , то отсюда не следует, что она имеет производную в этой точке. , то отсюда не следует, что она имеет производную в этой точке. Lưu ý: điều ngược lại là không đúng, nếu hàm liên tục tại điểm thì nó không theo đó mà nó có đạo hàm tại điểm này. Контрпример: 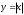 Утверждение: если функция имеет в точке правую и левую производную, то она непрерывна и справа и слева. Phát biểu: nếu một hàm số có đạo hàm bên phải và bên trái tại một điểm thì nó liên tục cả bên phải và bên trái. Контрпример: 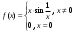  Геометрический смысл производной. Ý nghĩa hình học của đạo hàm. Теорема 1: График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке. Định lý 1: Đồ thị của hàm số có một tiếp tuyến không thẳng đứng khi và chỉ khi tại một điểm cho trước có một giá trị hữu hạn của đạo hàm của hàm số này.  х=х0+  Доказательство: Пусть существует значение f’( 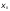 )-конечное, тогда )-конечное, тогда   при   Секущая стремится к касательной.  => =>  ч.т.д. ч.т.д.Пусть существует невертикальная касательная => существует  - конечный. - конечный.Секущая стремится к касательной. 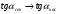 => =>  Касательная-предельное положение секущих. Дифференциал функции. Определение. Геометрический смысл. Hàm vi phân. Sự định nghĩa. ý nghĩa hình học. Дифференциал — это главная линейная часть приращения функции в точке. Vi phân là phần tuyến tính chính của gia số của một hàm tại một điểm.  Пусть функция y=f(x) диф в точке х:т.е. для её приращения выполняется Cho hàm số y = f (x) nghịch biến tại điểm x: tức là để tăng nó, Пусть функция y=f(x) диф в точке х:т.е. для её приращения выполняется Cho hàm số y = f (x) nghịch biến tại điểm x: tức là để tăng nó,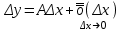 . Тогда . Тогда 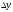 есть сумма двух слагаемых. Первое из них пропорционально есть сумма двух слагаемых. Первое из них пропорционально  , значит AΔx-линейная однородная функция от , значит AΔx-линейная однородная функция от  . Второе-бесконечно малая функция высшего порядка малости по сравнению с . Второе-бесконечно малая функция высшего порядка малости по сравнению с  . Если Ане=0, то второе слагаемое стремится к 0 при . Если Ане=0, то второе слагаемое стремится к 0 при  к 0 быстрее, чем первое, поэтому AΔx= f΄(x)Δx главный член приращения к 0 быстрее, чем первое, поэтому AΔx= f΄(x)Δx главный член приращения 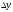 при при  к 0. Это слагаемое-диф функции(dy). По определению dy=df=f΄(x)Δx к 0. Это слагаемое-диф функции(dy). По определению dy=df=f΄(x)ΔxSau đó là tổng của hai số hạng. Giá trị đầu tiên của chúng tỷ lệ với, có nghĩa là AΔx là một hàm thuần nhất tuyến tính của. Thứ hai là một hàm nhỏ vô hạn của một bậc cao hơn của độ nhỏ so với. Nếu Ane = 0, thì số hạng thứ hai có xu hướng về 0 tại k nhanh hơn số hạng thứ nhất, do đó AΔx = f΄ (x) Δx là số hạng chính của số gia tại k 0. Số hạng này là vi phân của hàm số (dy ). Theo định nghĩa, dy = df = f΄ (x) Δx Геометрический смысл дифференциала: A и B – точки графика f(x), соответствующие значениям xo и (xo+Δx) независимой переменной. Ординаты точек A и B соответственно равны f(xo) и f(xo+Δx). Приращение функции Δf=f(xo+Δx)-f(xo) в точке xo равно длине отрезка BD и представимо в виде суммы Δf=BD=DC+CB, где DC=tgαΔx=f΄(xo)Δx и α есть угол между касательной в точке A к графику и положительным направлением оси x. Отсюда видно, что DC есть дифференциал функции f в точке xo: Ý nghĩa hình học của vi phân: A và B là các điểm thuộc đồ thị f (x) ứng với các giá trị xo và (xo + Δx) của biến độc lập. Các hoành độ của điểm A và B lần lượt bằng f (xo) và f (xo + Δx). Số gia của hàm Δf = f (xo + Δx) -f (xo) tại điểm xo bằng độ dài của đoạn thẳng BD và có thể được biểu diễn dưới dạng tổng Δf = BD = DC + CB, trong đó DC = tgαΔx = f΄ (xo) Δx và α là góc giữa tiếp tuyến tại điểm A với đồ thị và chiều dương của trục x. Điều này cho thấy DC là vi phân của hàm f tại điểm xo: DC=df=f΄(xo)Δx= tgαΔx; CB= Δf-df=  При этом на долю второго члена CB приращения Δf приходится величина  . Эта велич . Эта велич Диф и приращение независимой переменной равны между собой, но Δy=dy+  ина, при больших Δx, может быть даже больше, чем главный член, но она есть бесконечно малая более высокого порядка, чем Δx, когда Δx→0. Trong trường hợp này, số hạng thứ hai của số gia Δf là giá trị. Giá trị Dif này và số gia của biến độc lập bằng nhau, nhưng Δy = dy + nếu không, đối với Δx lớn, nó thậm chí có thể lớn hơn số hạng chính, nhưng nó là bậc cao hơn Δx khi Δx → 0. Диф функции f в точке х, соответствующий приращению Δx, есть приращение ординаты точки, лежащей на касательной (dy=CD) Производная f в x=отношению диф функции в этой точке к диф независимой переменной х Диф dx независ переменной не зависит от х, он= Δx-произвольному приращению аргумента х, а dy зависит от х и dx. Vi phân của hàm f tại điểm x, ứng với số gia Δx, là số gia của hoành độ của điểm nằm trên tiếp tuyến (dy = CD) Đạo hàm của f tại x = tỷ số giữa chênh lệch của hàm tại điểm đó với sai khác của biến độc lập x Dx khác biệt không phụ thuộc vào biến không phụ thuộc vào x, nó = Δx-gia số tùy ý của đối số x và dy phụ thuộc vào x và dx Необходимое и достаточное условие дифференцируемости. Điều kiện cần và đủ để tạo sự khác biệt. Если функция f дифференцируема в точке xo, то у неё существует производная и обратно  , где Δf=f(xo+Δx)-f(xo), , где Δf=f(xo+Δx)-f(xo), 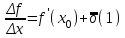 , ,  или или 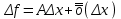 , где A=f΄(xo). где AΔx=df. , где A=f΄(xo). где AΔx=df. Определение: Пусть дана f(x), определенная в U(x0) и  такое, что х0+ такое, что х0+ принадлежит U(x0), тогда Δf=f(xo+Δx)-f(xo) и если ее приращение представимо в виде: принадлежит U(x0), тогда Δf=f(xo+Δx)-f(xo) и если ее приращение представимо в виде: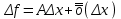 , где AΔx=df (*) то функция f дифференцируема в точке xo. , где AΔx=df (*) то функция f дифференцируема в точке xo.Nếu một hàm f khả vi tại một điểm xo thì nó có đạo hàm và ngược lại , trong đó Δf = f (xo + Δx) -f (xo), , hoặc là , trong đó A = f΄ (xo). trong đó AΔx = df. Định nghĩa: Cho f (x) xác định trong U (x0) cho trước và sao cho x0 + thuộc về U (x0) thì Δf = f (xo + Δx) -f (xo) và nếu số gia của nó có thể được biểu diễn là: , với AΔx = df (*) thì hàm f khả vi tại điểm xo. Определение. Sự định nghĩa. Функция 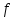 называется дифференцируемой в точке называется дифференцируемой в точке 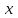 , если ее приращение можно представить в виде: , если ее приращение можно представить в виде: 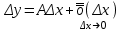 (2), Một hàm được gọi là có thể phân biệt tại một thời điểm nếu số gia của nó có thể được biểu thị như sau: (2), Một hàm được gọi là có thể phân biệt tại một thời điểm nếu số gia của nó có thể được biểu thị như sau: где А не зависит от  , но вообще зависит от , но вообще зависит от 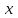 . trong đó A không phụ thuộc vào, nhưng nhìn chung phụ thuộc vào. . trong đó A không phụ thuộc vào, nhưng nhìn chung phụ thuộc vào.Необходимое(но не достаточное) условие дифференцируемости: если f дифференцируема в точке х0 , то f-непрерывна в х0. 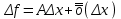 при при  следовательно функция непрерывна в х0 (обратное неверно) Điều kiện cần (nhưng không đủ) để phân biệt: nếu f khả vi tại x0 thì f liên tục tại x0. следовательно функция непрерывна в х0 (обратное неверно) Điều kiện cần (nhưng không đủ) để phân biệt: nếu f khả vi tại x0 thì f liên tục tại x0.và do đó hàm liên tục tại x0 (điều ngược lại không đúng) Если функция диф. в точке, то она непрерывна в этой точке, но не непрерывна в какой-то её окрестности. Nếu chức năng khác tại một điểm, sau đó nó liên tục tại điểm đó, nhưng không liên tục trong một số vùng lân cận của nó. Если существует конечная производная f΄(xo) в точке xo, то функция f(x) дифференцируема в этой точке. Nếu tại điểm xo tồn tại một đạo hàm hữu hạn f΄ (xo) thì hàm f (x) khả vi tại điểm này. Верно и обратное: если функция f дифференцируема в точке xo, т.е. ее приращение представимо в виде (*), то она имеет производную в точке xo, равную A: Điều ngược lại cũng đúng: nếu hàm f khả vi tại điểm xo, tức là Số gia của nó có thể được biểu diễn dưới dạng (*), khi đó nó có đạo hàm tại điểm xo bằng A: 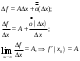 Теорема 1: Для того, чтобы функция была диф в точке х т.е., чтобы её приращение в этой точке представлялось по формуле 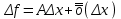 , необходимо и достаточно, чтобы она имела конечную производную в этой точке и тогда A=f΄(x) , необходимо и достаточно, чтобы она имела конечную производную в этой точке и тогда A=f΄(x) Định lý 1: Để hàm là một vi phân tại điểm x, tức là, gia số của nó tại điểm này được biểu diễn bằng công thức , điều cần thiết và đủ để nó có một đạo hàm hữu hạn tại điểm này, và khi đó A = f΄ (x) Доказательство: Достаточность условия доказана выше: из существования конечной производной 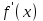 следовала возможность представления следовала возможность представления 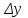 в виде в виде 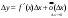 , где можно положить , где можно положить  . .Необходимость условия. Пусть функция 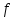 дифференцируема в точке дифференцируема в точке 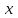 . Тогда из . Тогда из 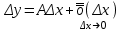 предполагая предполагая  , получаем , получаем 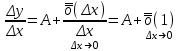 . .Предел правой части при 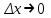 существует и равен А: существует и равен А:  . .Это означает, что существует производная  . Теорема доказана. . Теорема доказана.Bằng chứng: Sự đầy đủ của điều kiện đã được chứng minh ở trên: từ sự tồn tại của một đạo hàm hữu hạn tiếp theo là khả năng trình bày như nơi bạn có thể đặt Điều kiện cần thiết. Để chức năng có thể phân biệt ở một điểm . Sau đó từ giả định , chúng tôi nhận được. Giới hạn của phía bên phải tại tồn tại và bằng A: Điều này có nghĩa là có một đạo hàm . Định lý đã được chứng minh. |
