Определение модуля непрерывности функции на множестве. Примеры нахождения модуля непрерывности
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
Возрастание (убывание) функции в точке. Необходимое условие, достаточное условие возрастания (убывания) функции в точке. Экстремумы. Теорема Ферма. Chức năng tăng (giảm) tại một điểm. Điều kiện cần, điều kiện đủ để cơ năng tăng (giảm) tại một điểm. Cực trị. Định lý Fermat. Определение 1:. f(x) – возрастает (не убывает) tăng (không giảm)  , если , если 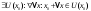 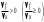 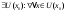 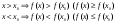 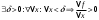 Определение 2. f(x) – убывает (не возрастает) giảm (không tăng) в точке  , если , если 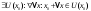 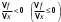 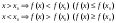 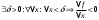 Теорема 1:(Необходимое условие возрастания (убывания) функции (Điều kiện cần để tăng (giảm) hàm  ) )Если f возрастает (убывает) в точке  и дифференцируема дифференцируема có thể phân biệt и дифференцируема дифференцируема có thể phân biệt   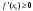  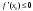 ) )Доказательство: Т.к. функция возрастает (убывает), то, по определению theo định nghĩa 1 , 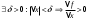 , а значит có nghĩa и , а значит có nghĩa и 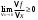 ( (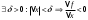 , а значит и , а значит и  ), теорема доказана. định lý được chứng minh. ), теорема доказана. định lý được chứng minh. Теорема 2: (Достаточное условие возрастания) (Đủ điều kiện để sinh trưởng) Если f(x) дифференцируема Nếu f (x) có thể phân biệt được в точке  , причем và , причем và 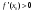 , то f(x) возрастает tăng в точке , то f(x) возрастает tăng в точке  . .Доказательство: 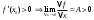 , значит по теореме о сохранении знака có nghĩa là theo định lý bảo toàn dấu hiệu : , значит по теореме о сохранении знака có nghĩa là theo định lý bảo toàn dấu hiệu : 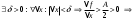 f возрастает. f возрастает.Замечание Nhận xét : если 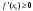 , то про возрастание сказать ничего нельзя. sau đó không thể nói gì về sự gia tăng. , то про возрастание сказать ничего нельзя. sau đó không thể nói gì về sự gia tăng. Теорема 2’: (Достаточное условие убывания) (Điều kiện đủ để giảm) Если f(x) дифференцируема Nếu f (x) có thể phân biệt được в точке  , причем , причем 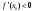 , то f(x) убывает в точке , то f(x) убывает в точке  . .Доказательство: По теореме о сохранении знака Theo định lý bảo toàn dấu : 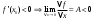 , значит có nghĩa , значит có nghĩa 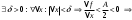 f(x) убывает. f(x) убывает.Замечание nhận xét : если 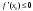 , то про убывание сказать ничего нельзя. sau đó không thể nói gì về sự giảm sút. , то про убывание сказать ничего нельзя. sau đó không thể nói gì về sự giảm sút. Экстремум-локальное свойство функции Thuộc tính địa phương cực đại của một hàm . Пусть дана точка x0 и существует U(x0), если для любого х принадл. U(x0) f(x)≤ f(x0), то x0-точка max, f(x)≥ f(x0), то x0-точка min Cho một điểm x0 đã cho và tồn tại U (x0) nếu, với x bất kỳ, U (x0) f (x) ≤ f (x0) thì x0-điểm max, f (x) ≥ f (x0), sau đó x0-point min Теорема Ферма:(Необходимое условие существования экстремума) Định lý Fermat: (Điều kiện cần thiết để tồn tại một điểm cực trị) Если f(x) дифференцируема có thể phân biệt в точке  и и  – точка локального экстремума điểm cực đại cục bộ, , то – точка локального экстремума điểm cực đại cục bộ, , то 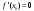 . .Доказательство: Пусть 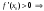 f(x) возрастает в точке f(x) возрастает в точке  , т.е. , т.е.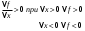 , т.е. , т.е.  – не точка экстремума. không phải là một điểm cực đoan. – не точка экстремума. không phải là một điểm cực đoan. Аналогично невозможен случай Tương tự, trường hợp 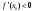 , следовательно kể từ đây , следовательно kể từ đây 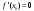 . . Теорема Ролля. Геометрический и физический смысл. Định lý Rolle. ý nghĩa hình học và vật lý. Теорема: Если функция 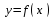 непрерывна на liên tục непрерывна на liên tục 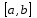 , дифференцируема на , дифференцируема на 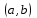 и и 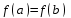 , то существует tồn tại точка , то существует tồn tại точка 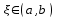 , такая, что , такая, что 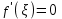 . .Доказательство: Так как функция f непрерывна на [a,b], то существует точка x1, в которой f достигает максимума и точка x2, в которой f достигает минимума. Рассмотрим 2 случая: Vì hàm f liên tục trên [a, b] nên có điểm x1 mà f đạt cực đại và điểm x2 mà f đạt cực tiểu. Hãy xem xét 2 trường hợp: Обе точки x1 и x2 совпадают с a или b Cả hai điểm x1 và x2 trùng với a hoặc b, , тогда  И тогда sau đó  производная phát sinh производная phát sinh 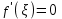 Одна из точек не является концевой отрезка [a,b] Một trong những điểm không phải là đoạn cuối [a, b] . Пусть 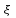 - та из них một trong số cchúng , которая - та из них một trong số cchúng , которая 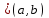 , тогда в точке , тогда в точке 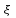 достигается локальный экстремум một cực điểm địa phương đã đạt được , кроме того Hơn thế nữa , достигается локальный экстремум một cực điểm địa phương đã đạt được , кроме того Hơn thế nữa , 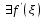 , так как по условию bởi vì theo điều kiện , так как по условию bởi vì theo điều kiện 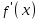 существует tồn tại существует tồn tại 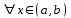 . Поэтому по теореме Ферма . Поэтому по теореме Ферма 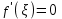 , что и требовалось доказать. cần được chứng minh. , что и требовалось доказать. cần được chứng minh. Контрпример 1:Уберем непрерывность в точке b: теорема потеряет силу т.к. нет точки, в которой касательная параллельна Ох Chúng ta hãy loại bỏ tính liên tục tại điểm b: định lý sẽ mất hiệu lực kể từ không có điểm nào mà tiếp tuyến song song  Контрпример 2:Уберем дифференцируемость в одной из точек: теорема потеряет силу т.к. нет точки, в которой касательная параллельна Ох Ví dụ 2: Hãy loại bỏ tính phân biệt ở một trong những điểm: định lý sẽ mất giá trị bởi vì không có điểm nào mà tiếp tuyến song song 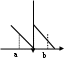 Контрпример3: убираем равенство на отрезках, нет точки, в которой 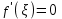 геометрический смысл: если выполнены все условия теоремы, то на графике функции 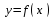 существует точка существует точка 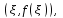 касательная в которой параллельна оси x. касательная в которой параллельна оси x.Ví dụ 3: chúng tôi loại bỏ sự bình đẳng trên các phân đoạn, không có điểm nào tại đó Ý nghĩa hình học: nếu thỏa mãn tất cả các điều kiện của định lý thì trên đồ thị của hàm số có một tiếp tuyến tại đó song song với trục x. 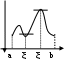 Физический смысл: при прямолинейном движении если перемещение тела = 0, то существует момент времени, в который скорость тела = 0. Ý nghĩa vật lý: trong chuyển động thẳng đều, nếu độ dời của vật = 0 thì tại thời điểm đó vận tốc của vật = 0 Теорема Коши. Физический смысл. Định lý Cauchy. ý nghĩa vật lý. Пусть функции f(x) и g(x) непрерывны на отрезке [a,b] и диференцируемые на интервале (a,b), одновременно не обращающиеся в ноль. Тогда на интервале (a,b) найдется точка ζ, для которой выполняется равенство: Để các hàm số f (x) và g (x) liên tục trên khoảng [a, b] và đồng biến trên khoảng (a, b), không biến mất cùng một lúc. Khi đó trên khoảng (a, b) có một điểm ζ mà đẳng thức là: 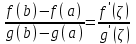 , a<ζ , a<ζДоказательство: g(b)-g(a)¹0 (что следует из условия g΄(x)¹0). Вводим функцию H(x)=(f(b)-f(a))·g(x)-(g(b)-g(a))·f(x). Очевидно, что она непрерывна на [a,b] и диференцируема на (a,b), т.к. f(b)-f(a) и g(b)-g(a) постоянны. Кроме того, H(a)=H(b), поэтому по теореме Ролля найдется такая точка ζ из (a,b), что H΄(ζ)=0. Chứng minh: g (b) -g (a) ¹0 (tuân theo điều kiện g΄ (x) ¹0). Chúng tôi giới thiệu hàm H (x) = (f (b) -f (a)) g (x) - (g (b) -g (a)) f (x). Rõ ràng, nó liên tục trên [a, b] và có thể phân biệt trên (a, b), bởi vì f (b) -f (a) và g (b) -g (a) là hằng số. Hơn nữa, H (a) = H (b), do đó, theo định lý Rolle, tồn tại một điểm ζ từ (a, b) sao cho H΄ (ζ) = 0. H΄(ζ)=(f(b)-f(a))·g΄(ζ)-(g(b)-g(a))·f΄(ζ)Þ(f(b)-f(a))·g΄(ζ)=(g(b)-g(a))·f΄(ζ) 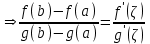 , т.к. по условию g(b)-g(a)¹0 и g΄(x)¹0 на (a,b). theo điều kiện g (b) -g (a) ¹0 và g΄ (x) ¹0 trên (a, b). , т.к. по условию g(b)-g(a)¹0 и g΄(x)¹0 на (a,b). theo điều kiện g (b) -g (a) ¹0 và g΄ (x) ¹0 trên (a, b). Физический смысл: Если f΄(x) и g΄(x) – скорости, то отношение перемещений равно отношению скоростей в какой-то момент времени. Ý nghĩa vật lý: Nếu f΄ (x) và g΄ (x) là vận tốc thì tỉ số độ dời bằng tỉ số vận tốc tại một thời điểm nào đó. Теорема Лагранжа. Геометрический и физический смысл. Формула конечных приращений. Định lý Lagrange. ý nghĩa hình học và vật lý. Công thức của số gia hữu hạn. Пусть функция 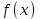 непрерывна на liên tục непрерывна на liên tục 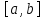 и диференцируема на và có thể phân biệt bằng и диференцируема на và có thể phân biệt bằng 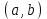 . Тогда существует на Sau đó tồn tại trên . Тогда существует на Sau đó tồn tại trên 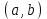 точка точка  , для которой выполняется mà sự bình đẳng равенство mà sự bình đẳng , для которой выполняется mà sự bình đẳng равенство mà sự bình đẳng 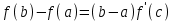 , причем , причем 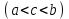 . .Доказательство: В теореме Коши, возьмем 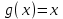 . Тогда . Тогда 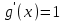 , ,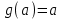 , , 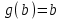 . .Из теоремы Коши: 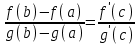  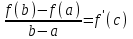 теорема доказана. định lý được chứng minh. теорема доказана. định lý được chứng minh. Физический смысл: f(b)–f(a)=S; b-a=t Найдется момент времени когда 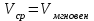 (средняя скорость равна мгновенной) (средняя скорость равна мгновенной) Ý nghĩa vật lý: f (b) –f (a) = S; b-a = t (tốc độ trung bình bằng tức thời) 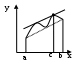 Геометрический смысл: Теорема Лагранжа утверждает, что если кривая есть график непрерывной на Cảm giác hình học: Định lý Lagrange phát biểu rằng nếu một đường cong là một đồ thị liên tục trên Геометрический смысл: Теорема Лагранжа утверждает, что если кривая есть график непрерывной на Cảm giác hình học: Định lý Lagrange phát biểu rằng nếu một đường cong là một đồ thị liên tục trên  функции, диференцируемой на có thể phân biệt bằng функции, диференцируемой на có thể phân biệt bằng  , то на этой кривой существует точка, соответствующая некоторой абсциссе , то на этой кривой существует точка, соответствующая некоторой абсциссе  такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой thì có một điểm trên đường cong này tương ứng với một số abscissa sao cho tiếp tuyến của đường cong tại điểm này song song với hợp âm co các đầu của đường cong такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой thì có một điểm trên đường cong này tương ứng với một số abscissa sao cho tiếp tuyến của đường cong tại điểm này song song với hợp âm co các đầu của đường cong 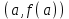 и и 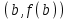 . .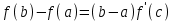 формула (Лагранжа) конечных приращений công thức (Lagrange) cho số gia hữu hạn. . Промежуточное значение giá trị trung gian 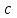 удобно записывать в виде nó là thuận tiện để viết trong biểu mẫu удобно записывать в виде nó là thuận tiện để viết trong biểu mẫu 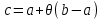 , где , где 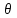 есть некоторое число, удовлетворяющее неравенствам Có một số thỏa mãn các bất đẳng thức есть некоторое число, удовлетворяющее неравенствам Có một số thỏa mãn các bất đẳng thức 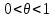 . Тогда формула Лагранжа примет вид Khi đó công thức Lagrange có dạng . Тогда формула Лагранжа примет вид Khi đó công thức Lagrange có dạng 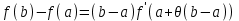 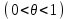 Она верна, очевидно, не только для Đó là sự thật, rõ ràng, không chỉ cho 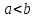 , но и для , но и для 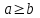 . .Условие монотонности функции на отрезке. Условие постоянства функции на отрезке. Điều kiện để tính đơn điệu của một hàm số trên một đoạn thẳng. Điều kiện không đổi của một hàm trên một đoạn. Определение: Sự định nghĩa Функция 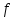 называется строго возрастающей на отрезке [a,b], если для любых точек được gọi là tăng nghiêm ngặt trên khoảng [a, b] nếu với bất kỳ điểm nào называется строго возрастающей на отрезке [a,b], если для любых точек được gọi là tăng nghiêm ngặt trên khoảng [a, b] nếu với bất kỳ điểm nào 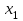 , , 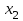 из [a,b], удовлетворяющих неравенству thỏa mãn bất đẳng thức из [a,b], удовлетворяющих неравенству thỏa mãn bất đẳng thức 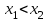 , имеет место неравенство chúng ta có sự bất bình đẳng , имеет место неравенство chúng ta có sự bất bình đẳng 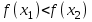 . .Определение: Функция 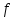 называется неубывающей на [a,b], если из того, что được gọi là không giảm trên [a, b] nếu từ thực tế rằng называется неубывающей на [a,b], если из того, что được gọi là không giảm trên [a, b] nếu từ thực tế rằng 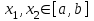 и и 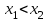 следует, что следует, что 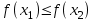 . .Определение: Функция 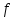 называется строго убывающей на отрезке [a,b], если из того, что được gọi là giảm nghiêm ngặt trên khoảng [a, b] nếu từ thực tế rằng называется строго убывающей на отрезке [a,b], если из того, что được gọi là giảm nghiêm ngặt trên khoảng [a, b] nếu từ thực tế rằng 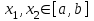 и и 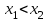 следует, что следует, что 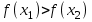 . . Определение: Функция 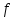 называется невозрастающей на [a,b], если из того, что được gọi là không gia tăng trên [a, b] nếu từ thực tế là называется невозрастающей на [a,b], если из того, что được gọi là không gia tăng trên [a, b] nếu từ thực tế là 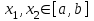 и и 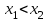 следует, что следует, что 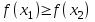 . .Пример: 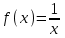 Если 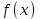 убывает на убывает на 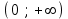 и на и на 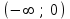 , то нельзя говорить, что , то нельзя говорить, что 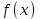 убывает на убывает на 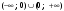 . .Теорема 1: (Достаточное условие возрастания (неубывания) и убывания (невозрастания) функции на отрезке) (Điều kiện đủ để các hàm tăng (không giảm) và giảm (không tăng) trên một đoạn) Если 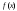 непрерывна на отрезке liên tục trên phân khúc непрерывна на отрезке liên tục trên phân khúc 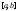 и дифференцируема на интервале và có thể phân biệt trong khoảng thời gian и дифференцируема на интервале và có thể phân biệt trong khoảng thời gian 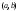 и и 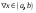 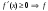 - неубывающая на - неубывающая на 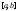 ko giảm ko giảm 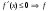 - невозрастающая на - невозрастающая на 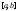 ko tăng ko tăng 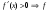 - возрастающая на - возрастающая на 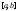 tăng tăng 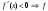 - убывающая на - убывающая на 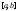 giảm giảm Доказательство: 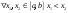 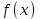 на отрезке trên phân khúc на отрезке trên phân khúc 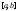 удовлетворяет теореме Лагранжа, т.е. thỏa mãn định lý Lagrange, tức là удовлетворяет теореме Лагранжа, т.е. thỏa mãn định lý Lagrange, tức là 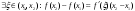 1) Т.к. 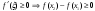 , т.е. функция – неубывающая. , т.е. функция – неубывающая.2), 3) и 4) доказываются аналогично. được chứng minh theo cách tương tự. Теорема доказана. Теорема 2: (Условие постоянства функции на отрезке) (Điều kiện đồng biến của hàm số trên khoảng) Если 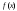 непрерывна на отрезке liên tục trên phân khúc непрерывна на отрезке liên tục trên phân khúc 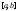 и дифференцируема на интервале và có thể phân biệt trong khoảng thời gian и дифференцируема на интервале và có thể phân biệt trong khoảng thời gian 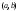 и и 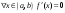 , то , то 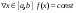 Доказательство: Зафиксируем точку Sửa một điểm 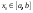 , тогда , тогда 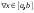 на отрезках trên các phân đoạn на отрезках trên các phân đoạn 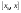 и и 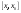 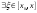 или или 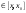 такое, что на этих отрезках будет выполняться теорема Лагранжа: такое, что на этих отрезках будет выполняться теорема Лагранжа: rằng trên các đoạn này, định lý Lagrange sẽ giữ nguyên: 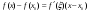 А т.к. 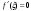 , ,  . .Теорема доказана. Достаточные условия экстремума. Điều kiện đủ cho một điểm cực trị. Теорема 1: (первое достаточное условие существования экстремума) (điều kiện đủ đầu tiên để tồn tại một điểm cực trị) Если 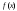 непрерывна в точке liên tục tại điểm непрерывна в точке liên tục tại điểm  дифференцируема в правой и левой có thể phân biệt ở bên phải và bên trái дифференцируема в правой и левой có thể phân biệt ở bên phải và bên trái 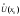 , , 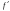 имеет разные знаки слева и справа от có các dấu hiệu khác nhau ở bên trái và bên phải của имеет разные знаки слева и справа от có các dấu hiệu khác nhau ở bên trái và bên phải của  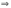  – точка экстремума. điểm cao nhất. – точка экстремума. điểm cao nhất. Доказательство: Т.к 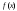 с одной стороны возрастает, с другой убывает, т.е. một mặt nó tăng, mặt khác nó giảm, tức là с одной стороны возрастает, с другой убывает, т.е. một mặt nó tăng, mặt khác nó giảm, tức là 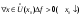 - max; - max; 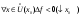 - min - minЗамечания: в самой точке х0 функция не обязательно должна быть диферен(х^(2/3)), непрерывность важна (хотя бы односторонняя) Nhận xét: tại chính điểm x0, hàm không phải là khác phương (x ^ (2/3)), tính liên tục là quan trọng (ít nhất là một phía) Теорема 2: (второе достаточное условие существования экстремума) Если функция дважды диф в точке Định lý 2: (điều kiện đủ thứ hai để tồn tại cực trị) Nếu hàm đồng biến kép tại một điểm  т.е. существует производная в U(x0), при этом tồn tại một đạo hàm trong U (x0), và т.е. существует производная в U(x0), при этом tồn tại một đạo hàm trong U (x0), và 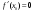 и и 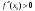 , то , то  - точка min; если - точка min; если 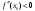 , то , то  - точка max - точка maxДоказательство: 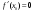 , существует tồn tại , существует tồn tại 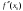  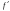 определена в được định nghĩa trong определена в được định nghĩa trong 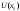 . .Рассмотрим 2 случая: Hãy xem xét 2 trường hợp: 1) 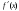 в точке в точке  возрастает ( возрастает (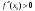 ) )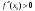 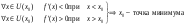 , ,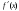 возрастает, возрастает, 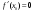 => =>2) 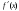 в точке в точке  убывает ( убывает (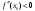 )0. )0.Формула Тейлора для многочленов. Công thức Taylor cho đa thức. Рассмотрим произвольный многочлен степени n: Xét một đa thức bậc n tùy ý: (1) 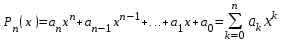 Пусть a – любое фиксированное число, тогда, полагая Đặt một số cố định bất kỳ, sau đó, 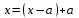 , получим chúng tôi nhận được , получим chúng tôi nhận được (2) 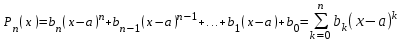 Это выражение называют разложение многочлена Biểu thức này được gọi là khai triển của đa t 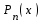 по степеням theo độ по степеням theo độ 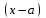 . Здесь . Здесь 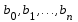 – числа, зависящие от là những con số phụ thuộc vào – числа, зависящие от là những con số phụ thuộc vào 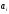 и и  , – коэффициенты разложения là hệ số mở rộng , – коэффициенты разложения là hệ số mở rộng 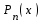 по степеням theo độ по степеням theo độ 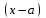 . . Подставим в выражение (2) Thay thế trong biểu thức (2) 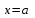 , получим , получим(3) 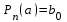 Найдем последовательные производные Hãy tìm các đạo hàm kế tiếp 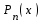 и подставим в них và đặt chúng vào и подставим в них và đặt chúng vào 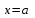 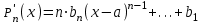 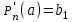 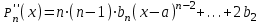 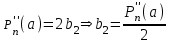 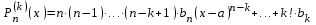 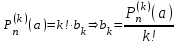 Пусть f(x) n раз диф в точке x0, тогда для неё pn(a)=f n(a) Gọi f (x) gấp n lần dif tại điểm x0, thì pn (a) = f n (a) 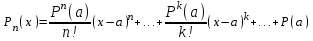 или 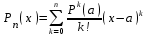 Последняя формула называется формулой Тейлора для многочлена Công thức cuối cùng được gọi là công thức Taylor cho đa thức 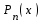 по степеням theo độ по степеням theo độ 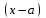 . Отметим, что правая часть этого выражения фактически не зависит от Lưu ý rằng phía bên phải của biểu thức này thực sự độc lập với . Отметим, что правая часть этого выражения фактически не зависит от Lưu ý rằng phía bên phải của biểu thức này thực sự độc lập với 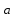 . . Формула Тейлора для дифференцируемых функций с остаточным членом в форме Лагранжа. Công thức của Taylor cho các hàm phân biệt với số hạng dư ở dạng Lagrange. Если функция f(x) n раз дифференцируема в точке а, то для нее существует многочлен (a=x0) Nếu một hàm f (x) khả vi n lần tại điểm a thì nó có một đa thức (a = x0) 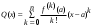 - это многочлен Тейлора n-го порядка функции f(x) в точке a. Обозначим за là đa thức Taylor bậc n của hàm f (x) tại điểm a. Biểu thị bởi - это многочлен Тейлора n-го порядка функции f(x) в точке a. Обозначим за là đa thức Taylor bậc n của hàm f (x) tại điểm a. Biểu thị bởi 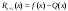 - на сколько многочлен отличается от самой функции đa thức khác với chính hàm bao nhiêu. . - на сколько многочлен отличается от самой функции đa thức khác với chính hàm bao nhiêu. . 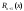 называют остаточным членом. Нужно доказать, что для «хороших» функций được gọi là phần dư. Chúng tôi cần chứng minh rằng đối với các chức năng "tốt" называют остаточным членом. Нужно доказать, что для «хороших» функций được gọi là phần dư. Chúng tôi cần chứng minh rằng đối với các chức năng "tốt" 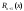 будет достаточно мало. Докажем теорему, которую сформулируем в конце. sẽ đủ nhỏ. Hãy để chúng tôi chứng minh định lý, mà chúng tôi xây dựng ở cuối. будет достаточно мало. Докажем теорему, которую сформулируем в конце. sẽ đủ nhỏ. Hãy để chúng tôi chứng minh định lý, mà chúng tôi xây dựng ở cuối. Рассмотрим функцию f; зафиксируем точку a, в которой будем раскладывать функцию, и произвольную точку x, такую что f(x) n-1 раз дифференцируема на [a,x] и n раз дифференцируема 1на (a,x). В точке а функция дифференцируема n-1 раз, значит для нее можно составить многочлен Тейлора n-1 порядка. Xét hàm f; chúng ta cố định một điểm a mà tại đó chúng ta sẽ khai triển hàm và một điểm x tùy ý sao cho f (x) phân biệt được n-1 lần trên [a, x] và n lần phân biệt được 1 trên (a, x). Tại điểm a, hàm khả vi n-1 lần, nghĩa là có thể lập một đa thức Taylor bậc n-1. 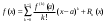 Представим Tưởng tượng 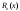 в виде như: : в виде như: :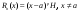 , где р – произвольное число, H – некоторая функция, зависящая от x. trong đó p là một số tùy ý, H là một số hàm phụ thuộc vào x. , где р – произвольное число, H – некоторая функция, зависящая от x. trong đó p là một số tùy ý, H là một số hàm phụ thuộc vào x. Рассмотрим функцию Xem xét chức năng : 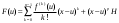 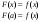 Рассмотрим F(u) на [a,x]: F(u) непрерывная на [a,x], дифференцируема на (a,x), F(x)=F(a) Xét F (u) trên [a, x]: F (u) liên tục trên [a, x], khả vi trên (a, x), F (x) = F (a) 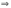 по теореме Ролля 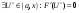 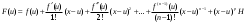 ; продифференцируем: hãy phân biệt: ; продифференцируем: hãy phân biệt:      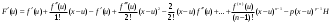 - и почти все взаимно уничтожается. - và hầu hết mọi thứ đều tiêu diệt lẫn nhau. - и почти все взаимно уничтожается. - và hầu hết mọi thứ đều tiêu diệt lẫn nhau. 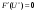 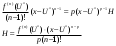 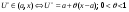 , тогда , тогда 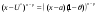 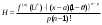 ; ; 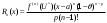 Подставим теперь p:=n; Thay ngay p: = n; Подставим теперь p:=n; Thay ngay p: = n; 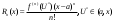 - это остаточный член в форме Лагранжа. Подставим теперь p:=1 - это остаточный член в форме Лагранжа. Подставим теперь p:=1 là số hạng còn lại ở dạng Lagrange. Thay thế ngay bây giờ p: = 1 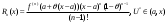 - это остаточный член в форме Коши. - это остаточный член в форме Коши. là số hạng còn lại ở dạng Cauchy. Теорема Если функция n-1 раз дифференцируема на [a,x], n раз на (a,x), то она раскладывается по формуле Тейлора с остаточными членами в форме Лагранжа и Коши. Если функция f(x) имеет непрерывную n-ю производную в точке а, то в окрестности точки а она раскладывается по формуле Тейлора с остаточными членами в форме Лагранжа, Коши и Пеано. Nếu một hàm phân biệt n-1 lần trên [a, x], n lần trên (a, x), thì nó được khai triển bởi công thức Taylor với các số hạng dư ở dạng Lagrange và Cauchy. Nếu hàm f (x) có đạo hàm cấp n liên tục tại điểm a, thì trong một lân cận của điểm a, nó được khai triển theo công thức Taylor với các số hạng dư dưới dạng Lagrange, Cauchy và Peano. Формула Тейлора для дифференцируемых функций с остаточным членом в форме Пеано. Единственность разложения. Công thức của Taylor cho các hàm phân biệt với số hạng dư ở dạng Peano. Tính duy nhất của sự phân hủy. Рассмотрим форму Лагранжа: Hãy xem xét dạng Lagrange: Пусть теперь f имеет непрерывную n-ю производную в точке а. Это означает, что на [a,x) функция n раз дифференцируема. Значит f(x) можно представить в виде: Bây giờ cho f có đạo hàm cấp n liên tục tại a. Điều này có nghĩa là trên [a, x) hàm phân biệt n lần. Vì vậy, f (x) có thể được biểu diễn dưới dạng: 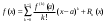 ; ; 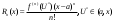 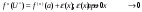 , т.к. производная непрерывна. Тогда bởi vì đạo hàm là liên tục. sau đó , т.к. производная непрерывна. Тогда bởi vì đạo hàm là liên tục. sau đó 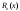 можно представить в виде: có thể được biểu diễn dưới dạng: можно представить в виде: có thể được biểu diễn dưới dạng: 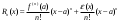 ; ; 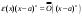 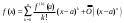 - это формула Тейлора с остаточным членом в форме Пеано. - это формула Тейлора с остаточным членом в форме Пеано. Таким образом, мы доказали следующую теорему: là công thức Taylor với số hạng dư ở dạng Peano. Như vậy, chúng ta đã chứng minh được định lý sau: Теорема (о единственности разложения функции по формуле Тейлора в форме Пеано) (về tính duy nhất của khai triển một hàm theo công thức Taylor ở dạng Peano) Если 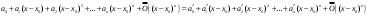 , то , то 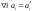 , , 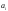 - коэффициенты из формулы Тейлора. Т.е. если есть какие-то другие коэффициенты hệ số từ công thức Taylor. Những thứ kia. nếu có bất kỳ hệ số nào khác - коэффициенты из формулы Тейлора. Т.е. если есть какие-то другие коэффициенты hệ số từ công thức Taylor. Những thứ kia. nếu có bất kỳ hệ số nào khác 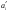 , то они тоже есть коэффициенты из формулы Тейлора: , thì chúng cũng là các hệ số từ công thức Taylor: , то они тоже есть коэффициенты из формулы Тейлора: , thì chúng cũng là các hệ số từ công thức Taylor: 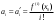 Доказательство. Устремим Hãy cố gắng 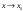 , получим, что , получим, что 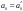 , т.к. , т.к. 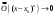 ; тогда ; тогда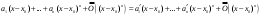 сократив на giảm bớt 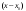 , получим: , получим: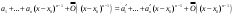 и опять же Và một lần nữa и опять же Và một lần nữa 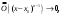 если если 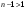 . . И так мы можем проделать до n-го коэффициента. Теорема доказана. Và vì vậy chúng tôi có thể làm đến hệ số thứ n. Định lý đã được chứng minh. Формула Маклорена для основных элементарных функций с остаточным членом в форме Пеано и Лагранжа Công thức Maclaurin cho các hàm cơ bản cơ bản với số hạng còn lại ở dạng Peano và Lagrange Общий вид формулы Тейлора для функций: Quan điểm chung về công thức Taylor cho các hàm: 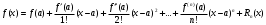 , где , где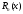 - остаточный член. thành viên dư. - остаточный член. thành viên dư. При 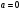 получаем так называемую формулу Маклорена. chúng tôi nhận được cái gọi là công thức Maclaurin. получаем так называемую формулу Маклорена. chúng tôi nhận được cái gọi là công thức Maclaurin. 1) 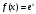 , , 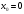 , , 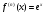 , , 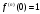 . Отсюда получаем, что Do đó chúng tôi nhận được điều đó . Отсюда получаем, что Do đó chúng tôi nhận được điều đó 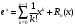 . . 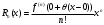 , ,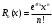 , где , где 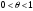 . И в итоге имеем Và cuối cùng chúng ta có : . И в итоге имеем Và cuối cùng chúng ta có : 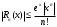 , , 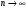 , , 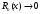 . .Пример: Пусть 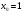 , тогда получим: , тогда получим: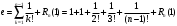 , , 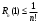 . .2) 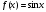 , ,Поскольку Trong chừng mực 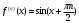 , , 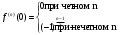 , формула имеет вид: công thức trông giống như: , формула имеет вид: công thức trông giống như:  , где n – нечётное число, а остаточный член в форме Лагранжа равен trong đó n là số lẻ, và số hạng còn lại ở dạng Lagrange là , где n – нечётное число, а остаточный член в форме Лагранжа равен trong đó n là số lẻ, và số hạng còn lại ở dạng Lagrange là 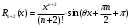 , , 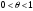 . .Очевидно, что для остаточного члена справедлива следующая оценка: Rõ ràng là ước tính sau đây hợp lệ cho thời hạn còn lại: 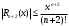 . .3) 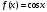 , , Поскольку Trong chừng mực 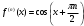 , то , то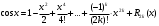 , , 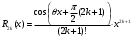 , ,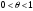 , , 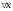 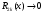 , , 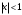 . .4) 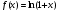 , ,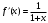 , , 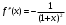 , , 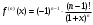 , , 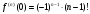 , ,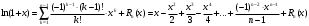 , ,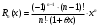 , , 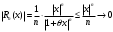 при при 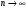 , ,Рассмотрим остаточный член в форме Коши: Xem xét số hạng còn lại ở dạng Cauchy: 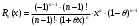 , , 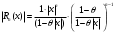 , , 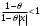 , ,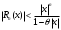 , где , где 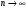 , , 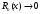 и и 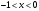 . .5) 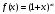 , ,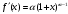 , , 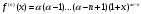 , , 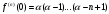 , ,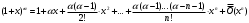 , ,Остаточный член в форме Пеано. Hạn dư ở dạng Peano. Разложения по формуле Тейлора в окрестности произвольной точки с помощью стандартных разложений. Taylor mở rộng trong vùng lân cận của một điểm tùy ý bằng cách sử dụng mở rộng tiêu chuẩn.   Вычисление пределов с помощью формулы Тейлора. Tính toán các giới hạn bằng công thức Taylor. 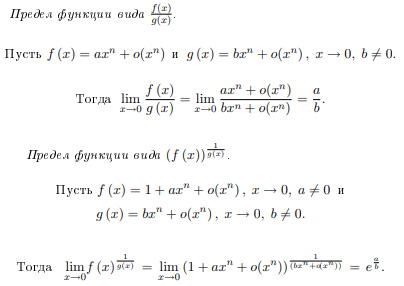 Выпуклость функции в точке. Достаточное условие. Выпуклость функции в точке. Достаточное условие. Определение: Функция f(x) называется выпуклой вверх (вниз) в точке xo, если найдется такая окрестность U(xo), что для всех точек из этой окрестности U(xo) график функции f(x) лежит не выше (не ниже) касательной, проведенной в точке xo. Định nghĩa: Hàm f (x) được gọi là lồi lên (xuống) tại một điểm xo nếu có lân cận U (xo) sao cho mọi điểm từ lân cận U (xo) này thì đồ thị của hàm f (x) nằm không cao hơn (không thấp hơn) tiếp tuyến vẽ tại điểm xo. З  амечание: Выпуклость в точке-локальное свойство функции, речь идёт об окрестности. Говорить о выпуклости в точке можно только если функция дифференцируема в этой точке. Lưu ý: Độ lồi tại một điểm là thuộc tính cục bộ của một hàm, chúng ta đang nói về một vùng lân cận. Có thể nói về độ lồi tại một điểm chỉ khi hàm có thể phân biệt được tại điểm này Контрпример: 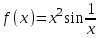 . 0 - ни точка выпуклости вверх, ни точка выпуклости вниз, ни точка перегиба, потому что в любой окрестности U(0) есть точки в которых функция выпукла вверх и вниз 0 không phải là điểm lồi lên, cũng không phải là điểm lồi xuống, cũng không phải là điểm uốn, bởi vì trong bất kỳ vùng lân cận nào của U (0) đều có điểm mà hàm lồi lên và xuống. . 0 - ни точка выпуклости вверх, ни точка выпуклости вниз, ни точка перегиба, потому что в любой окрестности U(0) есть точки в которых функция выпукла вверх и вниз 0 không phải là điểm lồi lên, cũng không phải là điểm lồi xuống, cũng không phải là điểm uốn, bởi vì trong bất kỳ vùng lân cận nào của U (0) đều có điểm mà hàm lồi lên và xuống.Теорема: (Достаточное условие выпуклости вверх (вниз) (Điều kiện đủ để độ lồi lên (xuống). Если функция f в U(xo) имеет непрерывную вторую производную Nếu hàm số f trong U (xo) có đạo hàm cấp hai liên tụcb  в точке xo, и при этом в точке xo, и при этом 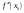 <0 (>0), то f выпукла в вверх (вниз) в точке xo. thì f lồi lên (xuống) tại điểm xo. <0 (>0), то f выпукла в вверх (вниз) в точке xo. thì f lồi lên (xuống) tại điểm xo. Доказательство: Т.к. функция f имеет непрерывную вторую производную hàm f có đạo hàm cấp hai liên tục 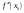 , то эта производная определена в некоторой окрестности , то эта производная определена в некоторой окрестности , thì đạo hàm này được xác định trong một số vùng lân cận 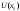 . Разложим функцию f по формуле Тéйлора с остаточным членом в форме Пеано: . Chúng ta khai triển hàm f theo công thức Taylor với số hạng dư ở dạng Peano: . Разложим функцию f по формуле Тéйлора с остаточным членом в форме Пеано: . Chúng ta khai triển hàm f theo công thức Taylor với số hạng dư ở dạng Peano: 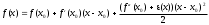 . .Причем функция 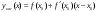 является графиком касательной к функции f в точке является графиком касательной к функции f в точке là đồ thị của tiếp tuyến của hàm số f tại điểm  . Поэтому если . Поэтому если 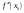 >0, то f(x)> >0, то f(x)>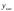 (x) в окрестности (x) trong khu phố (x) в окрестности (x) trong khu phố 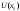 (т.к. ε(x)→0, при x→0), а если (т.к. ε(x)→0, при x→0), а если 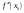 <0, то f(x)< <0, то f(x)< 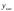 (x) в (x) в 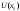 . .Точка перегиба. Достаточное условие. Điểm uốn. Đủ điều kiện. Определение. đnghia Точка 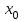 называется точкой перегиба, если в этой точке график переходит через сторону касательной (разные выпуклости слева и справа). называется точкой перегиба, если в этой точке график переходит через сторону касательной (разные выпуклости слева и справа). được gọi là điểm uốn nếu tại điểm này đồ thị đi qua cạnh của tiếp tuyến (các chỗ phồng khác nhau ở bên trái và bên phải). Замечание. NX Точка перегиба существует только если Điểm uốn chỉ tồn tại nếu 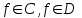 . Пример . Пример 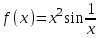 |
