Определение модуля непрерывности функции на множестве. Примеры нахождения модуля непрерывности
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
Интегрирование тригонометрических выражений. Рационализация. Tích phân các biểu thức lượng giác. Hợp lý hóa. Пусть  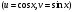 , где , где 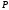 и и 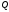 - многочлены от - đa thức từ - многочлены от - đa thức từ  и и  . .1) Если один из многочленов 1) Nếu một trong các đa thức  , ,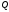 четный по thậm chí ở четный по thậm chí ở  , а другой – нечетный по , và cái còn lại là kỳ quặc trong , а другой – нечетный по , và cái còn lại là kỳ quặc trong  , то подстановка , sau đó thay thế , то подстановка , sau đó thay thế 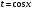 рационализирует интеграл. hợp lý hóa tích phân. рационализирует интеграл. hợp lý hóa tích phân. 2) Если один из многочленов Nếu một trong các đa thức 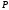 , ,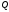 четный по thậm chí ở четный по thậm chí ở  , а другой – нечетный по và cái còn lại là kỳ quặc trong , а другой – нечетный по và cái còn lại là kỳ quặc trong  , то подстановка sau đó thay thế , то подстановка sau đó thay thế  рационализирует интеграл. hợp lý hóa tích phân. рационализирует интеграл. hợp lý hóa tích phân. 3) Если оба многочлена четные по Nếu cả hai đa thức là chẵn trong  и и  , то подстановка sau đó thay thế , то подстановка sau đó thay thế 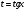 рационализирует интеграл. hợp lý hóa tích phân. рационализирует интеграл. hợp lý hóa tích phân. 3’) Выражения вида Biểu thức của dạng 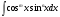 , где , где  и и  - четные. Они сходны с 3 случаем, где cũng. Chúng tương tự như trường hợp 3, trong đó - четные. Они сходны с 3 случаем, где cũng. Chúng tương tự như trường hợp 3, trong đó 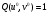 4) Универсальная подстановка. Thay thế phổ quát. Рационализация Hợp lý hóa 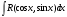 также достигается с помощью подстановки cũng đạt được bằng cách thay thế также достигается с помощью подстановки cũng đạt được bằng cách thay thế  , которая называется универсальной. В самом деле, , được gọi là phổ quát. Thật, , которая называется универсальной. В самом деле, , được gọi là phổ quát. Thật, 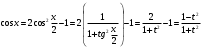 ; ; 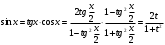 ; ; 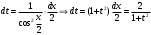  . .5) Выражения вида ) Biểu thức của biểu mẫu 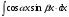 ; ; 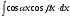 ; ; 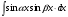 . Они рационализируются с помощью перевода в тригонометрические суммы. . Они рационализируются с помощью перевода в тригонометрические суммы. Chúng được hợp lý hóa bằng cách chuyển đổi thành các tổng lượng giác. Вычисление интегралов вида 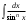 и и 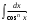 Tính tích phân dạng Tính tích phân dạng Интегрирование выражений, содержащих квадратичную иррациональность. Тригонометрические подстановки. Tích phân của biểu thức chứa vô tỉ bậc hai. Các phép thế lượng giác. Следующие интегралы превращаются в тригонометрические выражения при помощи тригонометрических подстановок: Các tích phân sau được chuyển thành biểu thức lượng giác bằng cách sử dụng các phép thay thế lượng giác:  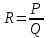 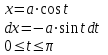 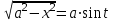 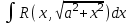 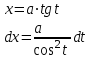 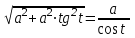  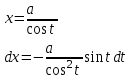 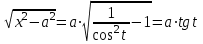 Пример: 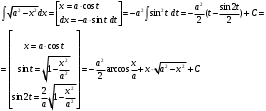 Интегрирование выражений вида 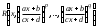 . Tích hợp các biểu thức của biểu mẫu . Tích hợp các biểu thức của biểu mẫuДокажем, что любой такой интеграл – берущийся в элементарных функциях. Hãy để chúng tôi chứng minh rằng bất kỳ tích phân nào như vậy được lấy trong các hàm cơ bản . Пусть 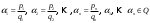 , т.к. , т.к. . Пусть m=НОК . Пусть m=НОК , ,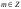 . Сделаем замену: Hãy thay thế: . Сделаем замену: Hãy thay thế: 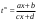 , тогда , тогда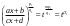 , причем последнее выражение - рациональное, т.к. m делится на любое và biểu thức cuối cùng là hợp lý, bởi vì m chia hết cho bất kỳ , причем последнее выражение - рациональное, т.к. m делится на любое và biểu thức cuối cùng là hợp lý, bởi vì m chia hết cho bất kỳ 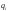 . .Тогда получим, что x=φ(t), dx=φ΄(t)dt, где φ(t) и φ΄(t)dt – рациональные выражения, поэтому: Khi đó chúng ta nhận được rằng x = φ (t), dx = φ΄ (t) dt, trong đó φ (t) và φ΄ (t) dt là các biểu thức hữu tỉ, do đó: 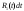 - тоже рациональное выражение cũng là một biểu thức hợp lý - тоже рациональное выражение cũng là một biểu thức hợp lý Подстановки Эйлера. Thay thế Euler. 1) 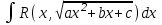 , где R-рациональная дробь. trong đó R là một phân số hữu tỉ. , где R-рациональная дробь. trong đó R là một phân số hữu tỉ. Пусть многочлен Cho đa thức 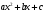 имеет вещественные корни. rễ thật. имеет вещественные корни. rễ thật. Пусть 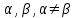 - корни GỐC , тогда - корни GỐC , тогда 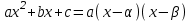 . .Рассмотрим подстановку Cân nhắc sự thay thế 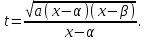 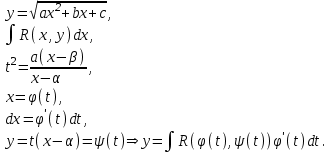 2) 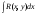 , где , где 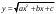 . .Корни трехчлена ax2+bx+c комплéксные. Тогда надо считать, что a>0, иначе трехчлен был бы отрицателен для всех x. Các nghiệm của tam thức ax2 + bx + c là phức. Sau đó, chúng ta phải giả sử rằng a> 0, nếu không thì tam thức sẽ âm với mọi x. 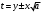 Thay .Возводя это равенство в квадрат и заменяя .So sánh sự bình đẳng này và thay thế Thay .Возводя это равенство в квадрат и заменяя .So sánh sự bình đẳng này và thay thế   его выражением, biểu hiện của nó, chúng tôi nhận được: получим:  его выражением, biểu hiện của nó, chúng tôi nhận được: получим: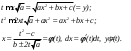 Где x, y и dx – некоторые рациональные функции от t. В конечном счете получаем: Trong đó x, y và dx là một số hàm hữu tỉ của t. Cuối cùng thì chúng tôi nhận được: 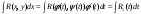 . .Типовые задачи Вычисление производных, в том числе с помощью предварительного дифференцирования. Найти второй дифференциал функции 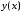 : : 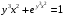 . .Найти производную порядка 2016 функции 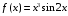 . .Разложить по формуле Тейлора в окрестности точки 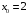 функцию функцию 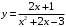 до п-го порядкас остаточным членом в форме Пеано, используя стандартное разложение. до п-го порядкас остаточным членом в форме Пеано, используя стандартное разложение.Вычисление интегралов. Упражнения к повышенному уровню Найти модуль непрерывности функций на множестве  : : а) 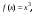 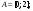 б) б) 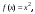 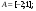 в) в) 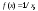 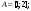 г) г) 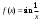 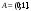 2. Верно ли утверждение: «Если функция дифференцируема в точке, то она непрерывна в некоторой окрестности этой точки» ? Если да, то доказать, если нет – привести пример. 3. Верно ли утверждение: «Если функция возрастает в точке, то она возрастает в некоторой окрестности этой точки»? Если да, то доказать, если нет – привести пример. 4. В каких случаях инвариантна форма: а) второго дифференциала; б) третьего дифференциала? 5. Для функции  вычислить вычислить 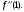 6. Решить уравнение 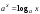 при при 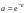 . .7. Пусть функции 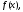 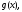 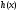 непрерывны на отрезке непрерывны на отрезке 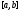 и дифференцируемы в интервале и дифференцируемы в интервале 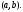 Доказать, что Доказать, что 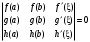 при некотором при некотором  8. Дифференцируемая функция 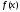 такова, что такова, что  Доказать, что существует точка Доказать, что существует точка 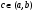 такая, что такая, что 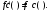 9. Доказать, что 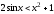 при всех при всех  О дифференцируемой функции  известно, что известно, что 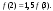 Доказать, что существует число Доказать, что существует число 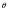 такое, что такое, что 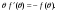 Пусть 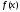 – дифференцируемая функция такая, что – дифференцируемая функция такая, что 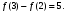 Доказать, что существует число Доказать, что существует число 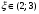 такое, что такое, что 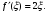 Определить, сколько действительных решений имеет уравнение 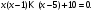 Функция 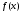 непрерывна на отрезке непрерывна на отрезке 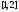 и дифференцируема на интервале и дифференцируема на интервале 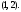 Доказать, что существует такое Доказать, что существует такое  что что 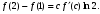 Найти 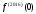 и и  если если 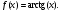 Для функции 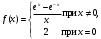 найти найти 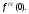 Найти 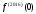 и и  если если 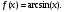 Найти 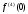 , если , если 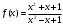 с помощью рекуррентной формулы. с помощью рекуррентной формулы. |
