Определение модуля непрерывности функции на множестве. Примеры нахождения модуля непрерывности
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
Замена переменной в неопределенном интеграле. Đổi biến trong tích phân bất định. 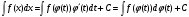 (1). (1).В этой формуле предполагается, что Công thức này giả định rằng  есть непрерывно дифференцируемая функция на некотором интервале изменения là một chức năng có thể phân biệt liên tục trên một số khoảng thời gian thay đổi есть непрерывно дифференцируемая функция на некотором интервале изменения là một chức năng có thể phân biệt liên tục trên một số khoảng thời gian thay đổi  , а , а 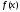 - непрерывная функция на соответствующем интервале или отрезке оси hàm liên tục trên khoảng hoặc đoạn tương ứng của trục - непрерывная функция на соответствующем интервале или отрезке оси hàm liên tục trên khoảng hoặc đoạn tương ứng của trục  . Докажем это утверждение. Слева в (1) стоит функция, которая является первообразной от . Докажем это утверждение. Слева в (1) стоит функция, которая является первообразной от Hãy chứng minh nhận định này. Ở bên trái trong (1) là một hàm là hàm chống đạo hàm của 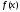 . Ее производная по . Dẫn xuất của nó đối với . Ее производная по . Dẫn xuất của nó đối với  равна: равна: Следовательно, если ввести в этой функции подстановку Do đó, nếu chúng tôi giới thiệu một sự thay thế trong chức năng này  , то получится первообразная от функции , sau đó chúng ta nhận được hàm antideriuctor của hàm , то получится первообразная от функции , sau đó chúng ta nhận được hàm antideriuctor của hàm 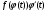 . Интеграл же справа есть, по определению, некоторая первообразная от . Tích phân bên phải, theo định nghĩa, là một số phản đạo hàm của . Интеграл же справа есть, по определению, некоторая первообразная от . Tích phân bên phải, theo định nghĩa, là một số phản đạo hàm của 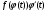 . Но две первообразные для одной и той же функции отличаются на некоторую постоянную Nhưng hai chất khử trùng cho cùng một chức năng khác nhau bởi một số hằng số . Но две первообразные для одной и той же функции отличаются на некоторую постоянную Nhưng hai chất khử trùng cho cùng một chức năng khác nhau bởi một số hằng số  . Это и записано в виде первого равенства (1). Что касается второго, то оно носит формальный характер - мы просто уславливаемся писать: . Это и записано в виде первого равенства (1). Что касается второго, то оно носит формальный характер - мы просто уславливаемся писать: . Điều này được viết dưới dạng đẳng thức đầu tiên (1). Đối với điều thứ hai, nó mang tính chất trang trọng - chúng tôi chỉ đơn giản đồng ý viết:  Пример: 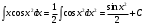 . .Интегрирование по частям. Tích hợp theo bộ phận. Пусть даны U и V, тогда по правилу интегрирования по частям Cho U và V, sau đó theo quy tắc tích phân từng phần 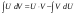  Пример 1: 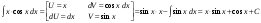 Пример 2: 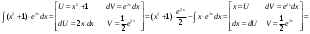  Пример 3: 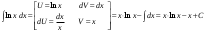 Пример 4:  Правило: При интегрировании выражений вида Khi tích phân các biểu thức có dạng  , где P(x)-многочлен, , trong đó P (x) là một đa thức, , где P(x)-многочлен, , trong đó P (x) là một đa thức, Если  за U принимаем cho U , chúng tôi lấy за U принимаем cho U , chúng tôi lấy Если  за U принимаем за U принимаем Пример5.  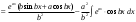 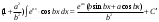 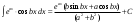 Интегрирование элементарных (простейших) дробей. Tích phân các phân số sơ cấp (đơn giản). 1. 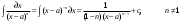 2.  n=1 n=1 4.  5 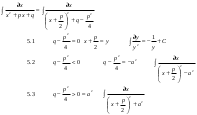 . . 6.  7.   8.  -случай 7 -случай 79. 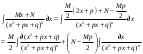 Случай 8. Случай 8.Интегрирование рациональных дробей. Tích phân phân số hữu tỉ. Пусть нужно найти неопределенный интеграл Hãy tìm tích phân bất định 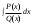 от рациональной действительной дроби. Если степень многочлена P k не меньше степени многочлена Q n từ một phân số thực hữu tỉ. Nếu bậc của đa thức P k không nhỏ hơn bậc của đa thức Q n ( ( от рациональной действительной дроби. Если степень многочлена P k не меньше степени многочлена Q n từ một phân số thực hữu tỉ. Nếu bậc của đa thức P k không nhỏ hơn bậc của đa thức Q n ( ( ), то прежде всего разделим P на Q : sau đó trước hết chúng ta chia P cho Q: ), то прежде всего разделим P на Q : sau đó trước hết chúng ta chia P cho Q:  Многочлен R интегрируется без труда, а Đa thức R được tích hợp mà không gặp khó khăn, và  – правильная действительная дробь. Все трудности сводятся к интегрированию правильной дроби, которую мы снова обозначим через là một phân số thực thích hợp. Tất cả những khó khăn liên quan đến việc tích phân một phân số thích hợp, mà chúng ta lại ký hiệu là – правильная действительная дробь. Все трудности сводятся к интегрированию правильной дроби, которую мы снова обозначим через là một phân số thực thích hợp. Tất cả những khó khăn liên quan đến việc tích phân một phân số thích hợp, mà chúng ta lại ký hiệu là 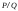 и представим в виде: và đặt nó ở dạng: и представим в виде: và đặt nó ở dạng:  Тогда пусть  , ,  1 случай. 1 trường hợp. Знаменатель содержит простые действительные корни, тогда его можно разложить на простейшие множители: (см.Теор.1) Mẫu số chứa các gốc thực đơn giản, sau đó nó có thể được phân tích thành các thừa số đơn giản: (xem Theor.1) 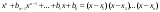 . Тогда . Тогда Приравнивая тождественно равные числители, получим: Bằng nhau các tử số giống nhau, chúng ta nhận được: 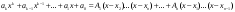 Существуют 2 метода нахождения Có 2 phương pháp để tìm 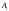 : :сравниваем коэффициенты при x с одинаковыми степенями; однако этот метод очень трудоемкий. so sánh các hệ số tại x với các lũy thừa giống nhau; tuy nhiên, phương pháp này rất tốn công sức. Т.к. равенства тождественны, можем взять Bởi vì sự bình đẳng giống hệt nhau, chúng ta có thể lấy  , тогда , тогда  . Так, подставляя поочередно . Vì vậy, lần lượt thay thế . Так, подставляя поочередно . Vì vậy, lần lượt thay thế 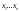 найдем все tìm mọi thứ найдем все tìm mọi thứ 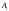 Т.о., мы получили сумму элементарных дробей, которые можем легко проинтегрировать. Như vậy, chúng ta đã có được tổng của các phân số sơ cấp, tích phân một cách dễ dàng. Пример 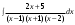 2 случай. TRƯỜNG HỢP 2 Знаменатель содержит кратные корни, тогда его можно представить в виде: Mẫu số chứa nhiều căn, sau đó nó có thể được biểu diễn dưới dạng:  . . Пусть существуют n различных корней с кратностями Cho có n căn phân biệt với các cấp số nhân 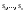 , тогда , тогда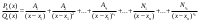 - и делаем все так же, как и в предыдущем примере. và làm mọi thứ theo cách tương tự như trong ví dụ trước. - и делаем все так же, как и в предыдущем примере. và làm mọi thứ theo cách tương tự như trong ví dụ trước. Пример 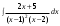 3 случай. TRƯỜNG HỢP 3 Знаменатель содержит кратные корни и многочлены, имеющие комплексные корни; Mẫu số chứa nhiều căn và đa thức có căn phức; 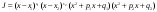 , где многочлены trong đó đa thức , где многочлены trong đó đa thức 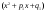 , ,  имеют комплексные корни. có rễ phức tạp. имеют комплексные корни. có rễ phức tạp. Тогда R(x) представим в виде: Khi đó R (x) có thể được biểu diễn dưới dạng: 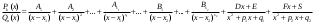 Снова приводим к общему знаменателю и приравниваем числители. Một lần nữa, chúng tôi giảm xuống một mẫu số chung và cân bằng các tử số. Пример  4 случай 4 trường hợp Знаменатель содержит кратные действительные и кратные комплексные корни; Mẫu số chứa nhiều căn thực và nhiều căn phức 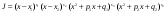 Тогда R(x) представим в виде: Khi đó R (x) có thể được biểu diễn dưới dạng:  А дальше все делаем по старой схеме: методом неопределенных коэффициентов находим A, B... Và sau đó chúng tôi làm mọi thứ theo sơ đồ cũ: bằng phương pháp hệ số không xác định, chúng tôi tìm thấy A, B … Пример 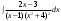 Теорема 1 Любой многочлен над полем С раскладывается на линейные и квадратичные множители с действительными коэффициентами: Bất kỳ đa thức nào trong trường C đều được phân tích thành nhân tử tuyến tính và nhân tử bậc hai với hệ số thực:  Доказательство Если 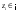 , то все в порядке : sau đó mọi thứ đều ổn , то все в порядке : sau đó mọi thứ đều ổn 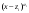 - линейный множитель с вещественными коэффициентами - hệ số nhân tuyến tính với hệ số thực - линейный множитель с вещественными коэффициентами - hệ số nhân tuyến tính với hệ số thực Пусть тогда существует невещественный корень Để rồi có một gốc không thực 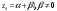 . Ему соответствует скобка Nó khớp với dấu ngoặc . Ему соответствует скобка Nó khớp với dấu ngoặc  . .Тогда если Sau đó nếu  – корень, то сопряженный к нему - một gốc, sau đó liên hợp với nó – корень, то сопряженный к нему - một gốc, sau đó liên hợp với nó  тоже будет корнем. Тогда наряду с множителем cũng sẽ là một gốc. Sau đó, cùng với hệ số тоже будет корнем. Тогда наряду с множителем cũng sẽ là một gốc. Sau đó, cùng với hệ số  будет присутствовать множитель sẽ có một hệ số будет присутствовать множитель sẽ có một hệ số  . Перемножим эти 2 скобки: . Hãy nhân 2 dấu ngoặc này: . Перемножим эти 2 скобки: . Hãy nhân 2 dấu ngoặc này: 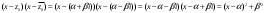 - квадратный трехчлен с вещественными коэффициентами, что и требовалось доказать. - квадратный трехчлен с вещественными коэффициентами, что и требовалось доказать. là một tam thức bình phương với các hệ số thực, đã được chứng minh. Теперь нам нужно доказать, что любые правильные дроби раскладываются на простейшие. Bây giờ chúng ta cần chứng minh rằng bất kỳ phân số thích hợp nào cũng có thể được chuyển thành những phân số đơn giản. Лемма 1 Bổ đề 1 Пусть многочлен Cho đa thức  представим в виде: hãy đặt nó ở dạng: представим в виде: hãy đặt nó ở dạng: 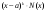 , где , где  - выделили максимальное кол-во скобок (x-a) đã chọn số lượng tối đa của dấu ngoặc (x-a) - выделили максимальное кол-во скобок (x-a) đã chọn số lượng tối đa của dấu ngoặc (x-a) и  - степень числителя меньше степени знаменателя, тогда - bậc của tử số nhỏ hơn bậc của mẫu số thì - степень числителя меньше степени знаменателя, тогда - bậc của tử số nhỏ hơn bậc của mẫu số thì 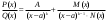 , причем дробь và phân số , причем дробь và phân số  - правильная; если - Chính xác; nếu như - правильная; если - Chính xác; nếu như 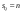 , то , то 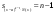 ; M(x) – многочлен с действительными коэффициентами. ; M (x) là một đa thức với hệ số thực. ; M(x) – многочлен с действительными коэффициентами. ; M (x) là một đa thức với hệ số thực. Доказательство Действуем так же, как в примерах: приводим к общему знаменателю и приравниваем числители: Chúng tôi hành động theo cách tương tự như trong các ví dụ: chúng tôi giảm xuống một mẫu số chung và cân bằng các tử số:  ; подставим thay thế ; подставим thay thế  , тогда , тогда 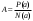 , по условию theo điều kiện , по условию theo điều kiện   - нам нужно доказать, что это – многочлен, а не дробь - Chúng ta cần chứng minh rằng đây là một đa thức, không phải là một phân số. . Подставим x=a, числитель при такой подстановке = 0, а это значит, что многочлен Thay x = a, tử số của thay thế đó = 0, có nghĩa là đa thức - нам нужно доказать, что это – многочлен, а не дробь - Chúng ta cần chứng minh rằng đây là một đa thức, không phải là một phân số. . Подставим x=a, числитель при такой подстановке = 0, а это значит, что многочлен Thay x = a, tử số của thay thế đó = 0, có nghĩa là đa thức  делится на chia делится на chia 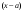 , т.е. M(x) – многочлен с действительными коэффициентами. là một đa thức với hệ số thực. , т.е. M(x) – многочлен с действительными коэффициентами. là một đa thức với hệ số thực. Теперь докажем, что дробь Bây giờ chúng ta chứng minh rằng phân số  - правильная, т.е. что - đúng, tức là gì - правильная, т.е. что - đúng, tức là gì  . .Степень знаменателя дроби = n-1, для числителя ( M(x)): по условию Bậc của mẫu số của phân số \ u003d n-1, đối với tử số (M (x)): theo điều kiện  и и  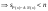 , да еще делим на và thậm chí chia cho (x-a) ( , да еще делим на và thậm chí chia cho (x-a) ( ), значит ), значит 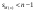 - меньше степени знаменателя, что и требовалось доказать. nhỏ hơn bậc của mẫu số, điều này đã được chứng minh. - меньше степени знаменателя, что и требовалось доказать. nhỏ hơn bậc của mẫu số, điều này đã được chứng minh. Лемма 2 Bổ đề 2 Если многочлен Q(x) имеет комплексный корень кратности k, т е представим в виде Nếu đa thức Q (x) có căn phức là bội k, tức là, chúng ta biểu diễn nó dưới dạng  , при этом многочлен trong khi đa thức , при этом многочлен trong khi đa thức  имеет только комплексные корни, которые не являются корнями N(x) . chỉ có các gốc phức không phải là gốc của N (x). имеет только комплексные корни, которые не являются корнями N(x) . chỉ có các gốc phức không phải là gốc của N (x).  , тогда дробь можно представить в виде: , thì phân số có thể được biểu diễn dưới dạng: , тогда дробь можно представить в виде: , thì phân số có thể được biểu diễn dưới dạng: 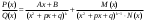 , причем вторая дробь будет правильной. M(x) – многочлен с действительными коэффициентами. , và phân số thứ hai sẽ đúng. M (x) là một đa thức với hệ số thực. , причем вторая дробь будет правильной. M(x) – многочлен с действительными коэффициентами. , và phân số thứ hai sẽ đúng. M (x) là một đa thức với hệ số thực. Доказательство Снова приведем дробь к общему знаменателю и приравняем числители. Получим Một lần nữa chúng ta đưa phân số về một mẫu số chung và quy đồng các tử số. Đến  Пусть  , , 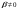 - корень многочлена - gốc đa thức - корень многочлена - gốc đa thức  , , 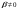 , значит сопряженное к нему , có nghĩa là liên hợp với nó , значит сопряженное к нему , có nghĩa là liên hợp với nó  тоже корень. Подставим cũng là một gốc. Thay thế тоже корень. Подставим cũng là một gốc. Thay thế  и и  : : 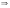  ; ;  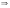 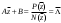 Найдем определитель системы, чтобы выяснить, имеет она решения, или нет: Hãy cùng tìm ra yếu tố quyết định của hệ thống để biết nó có giải pháp hay không: Найдем определитель системы, чтобы выяснить, имеет она решения, или нет: Hãy cùng tìm ra yếu tố quyết định của hệ thống để biết nó có giải pháp hay không: 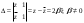 , значит, система разрешима и существуют A и B – решения системы, нужно доказать, что do đó hệ thống có thể giải được và có các nghiệm A và B của hệ thống, chúng ta cần chứng minh rằng , значит, система разрешима и существуют A и B – решения системы, нужно доказать, что do đó hệ thống có thể giải được và có các nghiệm A và B của hệ thống, chúng ta cần chứng minh rằng 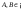  , заменим A и B на thay thế A và B bằng , заменим A и B на thay thế A và B bằng  : :  , решим сопряженную систему: giải quyết hệ thống liền kề: , решим сопряженную систему: giải quyết hệ thống liền kề:  - получили исходную систему; có hệ thống ban đầu; - получили исходную систему; có hệ thống ban đầu; так как столбец kể từ cột  - решение, столбец quyết định, cột - решение, столбец quyết định, cột  является решением. А т.к. решение должно быть единственным là giải pháp. Và kể từ khi giải pháp nên là duy nhất (определитель bản ngã является решением. А т.к. решение должно быть единственным là giải pháp. Và kể từ khi giải pháp nên là duy nhất (определитель bản ngã  ), ),  ; M(x) находится аналогично Лемме 1 ; теорема доказана. M (x) được tìm thấy tương tự với Bổ đề 1; định lý được chứng minh. ; M(x) находится аналогично Лемме 1 ; теорема доказана. M (x) được tìm thấy tương tự với Bổ đề 1; định lý được chứng minh. Обобщая все вышесказанное, получаем: («Теорему о разложении на простейшие дроби») Tổng hợp tất cả những điều trên, chúng ta nhận được: (“Định lý về phép phân tích thành phân số đơn giản”) Пусть многочлен Cho đa thức  представим в виде: hãy đặt nó ở dạng: представим в виде: hãy đặt nó ở dạng:  и положим và đặt и положим và đặt  , тогда , тогда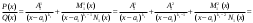  Заметим, что в самой последней дроби степень числителя (первая) меньше степени знаменателя (вторая) , т.е. последняя дробь – правильная. И каждую из дробей-слагаемых мы можем проинтегрировать в элементарных функциях. Lưu ý rằng ở phân số cuối cùng, bậc của tử số (thứ nhất) nhỏ hơn bậc của mẫu số (thứ hai), tức là phân số cuối cùng là đúng. Và chúng ta có thể tích hợp từng số hạng phân số trong các hàm cơ bản. Общий вывод:Любая рациональная дробь интегрируется в элементарных функциях. Kết luận chung: Mọi phân số hữu tỉ đều được tích phân trong các hàm số sơ cấp. |
