Определение модуля непрерывности функции на множестве. Примеры нахождения модуля непрерывности
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
Теорема 1 (Достаточное условие существования точки перегиба). (Điều kiện đủ để tồn tại điểm uốn).Если функция 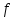 имеет Nó có имеет Nó có 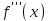 непрерывной LIÊN TỤC в точке непрерывной LIÊN TỤC в точке 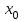 , , 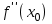 =0 и =0 и 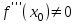 , то , то 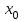 точка перегиба. điểm uốn. точка перегиба. điểm uốn. Доказательство: В этом случае : Trong trường hợp này 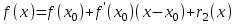 , , 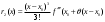 ) (формула Тейлора) , или ) (формула Тейлора) , или 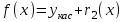 . .В силу непрерывности Do tính liên tục  в в 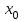 и того факта, что và thực tế là и того факта, что và thực tế là 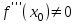   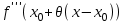 сохраняет знак в некоторой окрестности точки bảo tồn biển báo trong một số khu vực lân cận của điểm сохраняет знак в некоторой окрестности точки bảo tồn biển báo trong một số khu vực lân cận của điểm 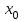 . С другой стороны, множитель Mặt khác, hệ số nhân . С другой стороны, множитель Mặt khác, hệ số nhân  меняет знак при переходе dấu hiệu thay đổi khi chuyển đổi меняет знак при переходе dấu hiệu thay đổi khi chuyển đổi 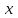 через через 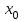 , а вместе с ним и величина , а вместе с ним и величина và cùng với nó là giá trị 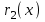 (равная превышению точки кривой над касательной в (равная превышению точки кривой над касательной в 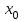 ) меняет знак при переходе ) меняет знак при переходе 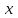 через через 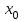 . (bằng phần dư của điểm đường cong trên tiếp tuyến trong . (bằng phần dư của điểm đường cong trên tiếp tuyến trong) thay đổi dấu hiệu khi đi qua Теорема доказана. Общая теорема об экстремумах и точках перегиба. Định lý tổng quát về điểm cực trị và điểm uốn. Теорема:Пусть функция 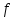 обладает следующими свойствами: có các thuộc tính sau обладает следующими свойствами: có các thuộc tính sau 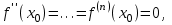 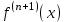 непрерывна tiếp diễn в непрерывна tiếp diễn в 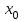 и и 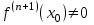 . Тогда, если . Тогда, если 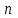 - нечетное число, то кривая số lẻ, sau đó là đường cong - нечетное число, то кривая số lẻ, sau đó là đường cong 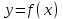 обращена выпуклостью вверх или вниз в зависимости от того, будет ли phồng lên hoặc xuống, tùy thuộc vào việc обращена выпуклостью вверх или вниз в зависимости от того, будет ли phồng lên hoặc xuống, tùy thuộc vào việc 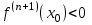 или или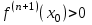 , а если , а если 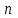 четное, то четное, то 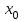 есть точка перегиба кривой. есть точка перегиба кривой. có một điểm uốn của đường cong. Доказательство: 1) Разложим по формуле Тейлора: Chúng tôi mở rộng theo công thức Taylor: 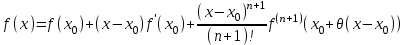 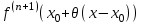 того же знака, cùng một dấu hiệu что того же знака, cùng một dấu hiệu что 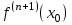 , ,  , , 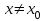 , если , если 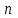 - нечетное то - нечетное то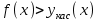 или или   всегда, всегда, 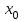 - не точка перегиба. không phải là một điểm uốn. - не точка перегиба. không phải là một điểm uốn. Если 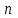 - четная - четная  С одной стороны Ở một bên 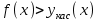 , с другой стороны , с другой стороны   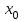 - точка перегиба. - точка перегиба. 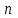 - четное. - четное.2) 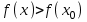 , , 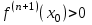 - min - min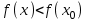 , , 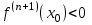 - max - maxПравило Лопиталя. Случай  . Раскрытие неопределенностей различных видов с помощью правила Лопиталя. Quy tắc của L'Hopital. Đang xảy ra . Раскрытие неопределенностей различных видов с помощью правила Лопиталя. Quy tắc của L'Hopital. Đang xảy ra. Tiết lộ các loại độ không chắc chắn khác nhau bằng cách sử dụng quy tắc của L'Hopital. Теорема 1:(Неопределенность вида 0/0) (Dạng không chắc chắn 0/0) Пусть f(x) и g(x) дифференцируемы в некоторой окрестности точки а Để f (x) và g (x) là phân biệt trong một số lân cận của điểm a ,  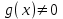 в этой окрестности и trong lĩnh vực này và в этой окрестности и trong lĩnh vực này và  в той же окрестности, тогда, если trong cùng một vùng lân cận, sau đó nếu в той же окрестности, тогда, если trong cùng một vùng lân cận, sau đó nếu 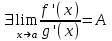 , то , то  Доказательство: 1) a – конечное. Доопределим функции: f(a)=0 и g(а) = 0; f(x) и g(x) непрерывны на [a;x] 1) a là hữu hạn. Hãy mở rộng các hàm: f (a) = 0 và g (a) = 0; f (x) và g (x) liên tục trên [a; x] 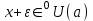 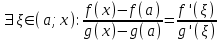 при при  f(a)=g(a)=0 => 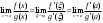 2) 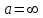 Пусть 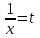 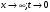 Введем функции Chúng tôi giới thiệu các HS  и и 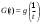 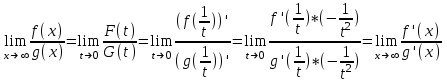 Теорема доказана. Замечание: обратное неверно, т.е. из существования предела функций не следует существование предела производных. Lưu ý: điều ngược lại không đúng, tức là sự tồn tại của một giới hạn của các hàm không bao hàm sự tồn tại của một giới hạn của các đạo hàm. Контрпример:  Теорема: Пусть функции f и g определены и дифференцируемы в некоторой окрестности точки a и Để các hàm f và g được xác định và phân biệt được trong một số lân cận của điểm a và 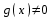 и и 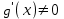 в некоторой выколотой окрестности точки a, тогда, если trong một số vùng lân cận bị thủng của điểm a, thì nếu в некоторой выколотой окрестности точки a, тогда, если trong một số vùng lân cận bị thủng của điểm a, thì nếu 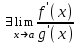 , то , то 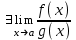 и и 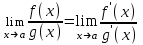 Доказательство: Возьмем произвольную последовательность Thực hiện một trình tự tùy ý  , , 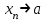 , , 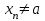 , тогда по определению предела по Гейне sau đó theo định nghĩa của giới hạn Heine , тогда по определению предела по Гейне sau đó theo định nghĩa của giới hạn Heine 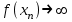 и и 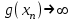 Тогда 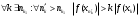 - для f(x) определение предела вида |f(x)|>C, где C = - для f(x) определение предела вида |f(x)|>C, где C = - đối với f (x) định nghĩa giới hạn có dạng | f (x) |> C, trong đó C =   - аналогично для g(x) - tương tự cho g (x) - аналогично для g(x) - tương tự cho g (x) Тогда можно найти такой номер, для которого будут выполняться оба неравенства: Sau đó, bạn có thể tìm thấy một số mà cả hai bất đẳng thức sẽ đúng:  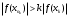 , ,  Используя термины Sử dụng các điều khoản 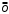 можно записать: можно записать: 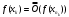 , , 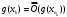 Пояснение: Giải trình: Пояснение: Giải trình: 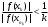 , а т.к. , а т.к. 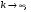 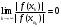 Найдем теперь предел отношения Bây giờ chúng ta hãy tìm giới hạn của mối quan hệ  к к 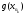 : :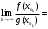 [ можно добавить или отнять [có thể được thêm hoặc bớt [ можно добавить или отнять [có thể được thêm hoặc bớt 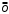 , предел от этого не изменится ] , giới hạn sẽ không thay đổi so với điều này] , предел от этого не изменится ] , giới hạn sẽ không thay đổi so với điều này]  [ воспользуемся теоремой Коши [ воспользуемся теоремой Коши [sử dụng định lý Cauchy: :  или или  - смотря, что больше] - cái nào lớn hơn] - смотря, что больше] - cái nào lớn hơn] 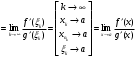 - по определению предела по Гейне. theo định nghĩa của giới hạn Heine. - по определению предела по Гейне. theo định nghĩa của giới hạn Heine. Мы получили еще не совсем теорему о сходимости последовательности через подпоследовательности, ( ее формулировка: если Chúng tôi vẫn chưa thu được một định lý về sự hội tụ của một dãy theo các dãy con, (công thức của nó: nếu 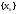 такова, что из любой её подпоследовательности такова, что из любой её подпоследовательности như vậy có phải từ bất kỳ chuỗi con nào của nó không 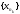 можно извлечь в свою очередь подпоследовательность можно извлечь в свою очередь подпоследовательность có thể trích xuất lần lượt một dãy con  , сходящуюся к конечному или бесконечному А , сходящуюся к конечному или бесконечному А , hội tụ đến A hữu hạn hoặc vô hạn, thì giới hạn , то предел 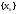 =А) мы пока что только из самой последовательности выделили сходящуюся подпоследовательность, а это еще не значит, что сама последовательность сходится. =А) мы пока что только из самой последовательности выделили сходящуюся подпоследовательность, а это еще не значит, что сама последовательность сходится. cho đến nay chúng ta chỉ chọn ra một dãy con hội tụ từ chính dãy, và điều này không có nghĩa là bản thân dãy hội tụ. Теперь возьмем произвольную последовательность Bây giờ lấy một chuỗi tùy ý 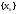 и её произвольную подпоследовательность và dãy con tùy ý của nó и её произвольную подпоследовательность và dãy con tùy ý của nó 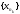 , тогда по только что доказанному из подпоследовательности , sau đó bằng những gì vừa được chứng minh từ hệ con , тогда по только что доказанному из подпоследовательности , sau đó bằng những gì vừa được chứng minh từ hệ con 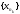 мы можем выделить подпоследовательность chúng ta có thể chọn một dãy con мы можем выделить подпоследовательность chúng ta có thể chọn một dãy con  , сходящуюся к , hội tụ với , сходящуюся к , hội tụ với  , т. е. , т. е.  Теперь мы взяли произвольную последовательность, поэтому Bây giờ chúng tôi đã thực hiện một trình tự tùy ý, vì vậy 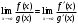 Причем важно, чтобы предел отношения производных существовал. Hơn nữa, điều quan trọng là giới hạn của tỷ lệ các dẫn xuất tồn tại. Теорема доказана. Раскрытие неопределенностей вида Tiết lộ sự không chắc chắn của biểu mẫu 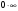 , ,  , , , , , ,  . .Кроме неопределенностей Vượt lên trên những điều không chắc chắn 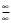 и и  , встречаются неопределенности вида có những điểm không chắc chắn về hình thức , встречаются неопределенности вида có những điểm không chắc chắn về hình thức 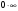 , , , , , , , ,  , определение которых очевидно. Эти неопределенности сводятся к неопределенностям , определение которых очевидно. Эти неопределенности сводятся к неопределенностям 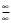 или или  алгебраическими преобразованиями. алгебраическими преобразованиями. , định nghĩa của ai là hiển nhiên. Những độ không chắc chắn này được giảm xuống thành độ không chắc chắn Неопределенность Tính không chắc chắn 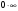 ( ( при при 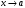 ). ). Ясно, что 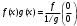 или или 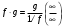 . .Неопределенности вида Nhập các điểm không chắc chắn  , ,  , ,  для выражения để diễn đạt для выражения để diễn đạt 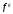 сводятся к неопределенности giảm đến mức không chắc chắn сводятся к неопределенности giảm đến mức không chắc chắn 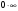 . . Согласно определению этой функции Theo định nghĩa của hàm này  . . 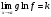 , то , то  . .Неопределенность Tính không chắc chắn  ( (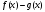 , , 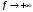 , , 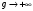 при при 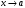 ) ) Легко видеть, что Có thể dễ dàng nhận thấy rằng 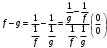 . .Первообразная. Неопределенный интеграл. Свойства. Nguyên thủy. Không xác định, không thể thiếu. Tính chất. Определение 1: Функция F называется первообразной функции f на (a,b), если функция F диф на интервале (a,b), и для всех x из этого интервала выполняется равенство: F΄(x)=f(x). Định nghĩa 1: Hàm F được gọi là đạo hàm của f trên (a, b) nếu hàm F đồng biến trên khoảng (a, b) và với mọi x từ khoảng này thì đẳng thức sau đây là: F΄ (x) = f (x). Замечание: Вместо (a,b) можно рассматривать [a,b], (a,b] и [a,b), но нужно будет говорить про односторонние производные: Lưu ý: Thay vì (a, b), bạn có thể xem xét [a, b], (a, b] và [a, b), nhưng bạn sẽ cần nói về đạo hàm một phía  =f(a), и =f(a), и 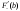 =f(b). =f(b).Пример  . .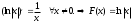 на промежутке (-∞,0) и на (0,+∞). trên khoảng (-∞, 0) và trên (0, + ∞). на промежутке (-∞,0) и на (0,+∞). trên khoảng (-∞, 0) và trên (0, + ∞). Теорема:(О множестве всех первообразных). Định lý: (Trên tập hợp tất cả các đạo hàm). Пусть F(x) является первообразной функции f(x) на промежутке I{(a,b) [a,b] (a,b] [a,b) }, тогда функции вида F(x)+C и только они являются первообразными функции f(x), где C – произвольная константа. Gọi F (x) là đạo hàm của f (x) trên khoảng I {(a, b) [a, b] (a, b] [a, b)} thì hàm có dạng F (x) + C và chỉ chúng là các đạo hàm của hàm f (x), trong đó C là một hằng số tùy ý. Доказательство: Пусть функция F(x) – первообразная функции f(x), тогда F΄(x)=f(x) и (F(x)+C)΄=f(x). Пусть функции F и G – первообразные функции f(x) на промежутке I (нужно доказать, что они отличаются на константу). Тогда (F-G)΄=0 Gọi hàm F (x) là đạo hàm của hàm f (x) thì F΄ (x) = f (x) và (F (x) + C) ΄ = f (x). Gọi hàm F và G là các đạo hàm của f (x) trên khoảng I (cần chứng minh rằng chúng khác nhau một hằng số). Khi đó (F-G) ΄ = 0 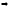 F-G=C (по теореме о функции, имеющей нулевую производную). F-G = C (theo định lý hàm số có đạo hàm bằng 0). F-G=C (по теореме о функции, имеющей нулевую производную). F-G = C (theo định lý hàm số có đạo hàm bằng 0). Теорема доказана. Определение 2: Множество всех первообразных функции f(x) на промежутке I называется неопределенным интегралом и обозначается Định nghĩa 2: Tập hợp tất cả các đạo hàm của hàm số f (x) trên khoảng I được gọi là tích phân bất định và được kí hiệu là  . При этом если функция F(x) – первообразная функции f(x), то Hơn nữa, nếu hàm F (x) là đạo hàm của hàm f (x) thì . При этом если функция F(x) – первообразная функции f(x), то Hơn nữa, nếu hàm F (x) là đạo hàm của hàm f (x) thì 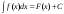 . .Пример:  . .Свойства первообразных и неопределенного интеграла. Tính chất của đạo hàm và tích phân bất định. 1. Пусть функция f(x) имеет первообразную F(x) на промежутке I и функция g(x) имеет первообразную G(x) на промежутке I, тогда функция f(x)±g(x) будет иметь первообразную F(x)±G(x) на промежутке I. Для интегралов: 1. Để hàm số f (x) có đạo hàm F (x) trên khoảng I và hàm số g (x) có đạo hàm G (x) trên khoảng I thì hàm số f (x) ± g (x ) sẽ có đạo hàm F (x) ± G (x) trên khoảng I. Đối với tích phân  +C +CЗамечание: Обратное неверно! Из существования интеграла Lưu ý: Điều ngược lại là không đúng! Từ sự tồn tại của tích phân 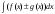 не следует существование интегралов sự tồn tại của tích phân không tuân theo  и и . .2. Первообразной функции k·f(x) является функция k·F(x). Для интегралов: 2. Đạo hàm của hàm k · f (x) là hàm k · F (x). Đối với tích phân: 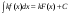 . .3. Т.к. f(x)-первообразная для f΄(x), то 3. Vì f (x) -đạo hàm cho f΄ (x) thì 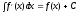 . .4. 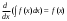 (слева производная) (đạo hàm bên trái) (слева производная) (đạo hàm bên trái) |
