1 Неопред БИ 12. 1. Неопределенность информации

• Название: 1. Неопределенность информации
• Дата: 19.09.2018
• Размер: 1.17 Mb.
• Имя файла: 1 Неопред БИ 12.doc
• Тип: Документы; #51096
• страница: 1 из 6

1. Неопределенность информации \

Факторы, обусловливающие необходимость учета фактора неопределенности многообразны.

• Характеристики некоторых товаров, приобретаемых потребителем, изначально не могут быть точно определены в момент покупки. Например, это касается рискованности и доходности ценных бумаг, выпускаемых компаниями.

• К неопределенности приводит действие внешних факторов (states of the world, state of Nature ) влияющих на выбор, осуществляемый индивидом, но никак от него не зависящих. Например, это может касаться регулятивных, правовых, коньюнктурных и пр. изменений, непосредственно затрагивающих деятельность компании и интересы акционеров.

• Неопределенность может порождаться непредсказуемым поведением контрагентов, например, благосостояние инвесторов в существенной степени зависит от того, насколько эффективным будет руководство компанией, осуществляемое менеджерами, от того окажется политика, проводимая Советом директоров компании и в какой в какой степени, она сможет препятствовать возможным злоупотреблениям со стороны высших менеджеров и пр.

Теоретические концепции поведения экономических агентов в условиях неопределенности и их тестирование. «Рамочные» эффекты.

Принимая решение в условиях неопределенности, индивид всегда участвует в своего рода лотерее. Например, покупая некую акцию, инвестор может как получить значительный выигрыш, так и лишиться инвестированных средств Обозначив через x_i исходы в такого рода лотерее, мы можем записать эту лотерею следующим образом

L₁ р о х₁ (1 - р) о х₂,

что означает: "Индивид с вероятностью р получит приз х₁и с вероятностью (1 - р) - приз х₂" Альтернативой участию в этой лотерее может быть покупка иной акции

L₂ q о х₃ (1 - q) о х₄

Какую из этих двух лотерей предпочтет индивид? При совпадении перечня исходов(призов) в обеих лотереях (х₁= х₃; х₂= х₄ ) ответ на этот вопрос может быть обусловлен вероятностным распределением выигрышей. Изменив вероятности получения призов в сторону увеличения вероятности получения лучшего приза, мы получим новую лотерею, которая будет стохастически доминировать исходную (более подробно о стохастическом доминировании будет сказано позднее). Но это отнюдь не снимает проблему ранжирования лотерей при отсутствии четко выраженного стохастического доминирования, столь частого при большем количестве возможных исходов.

Лотереи. Сведение сложных лотерей к простым.

Простая лотерея может быть описана как вектор вероятностей выпадения возможных исходов: L(р)=(р₁, р₂ , ... , р_n), где _i p _i =1 и p _i ≥ 0 для всех i =1, ... , n.

Геометрически простая лотерея соответствует точке на (n -1)-мерном симплексе 

Рис.1.1. n = 2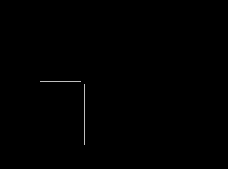



Рис.1.2. n = 3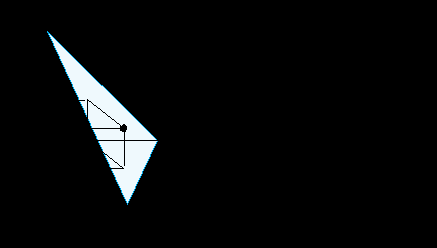



Сложные лотерии (compound lotteries)- в отличие от простых лотерей - допускают возможность рассмотрения в качестве возможных исходов не только получение индивидом неких конкретных "призов", но так называемых "вторичных" лотерей. Сложной, например, является лотерея, включающая в перечень возможных призов билеты следующего тура этой лотереи.

Математически сведение сложной лотереи к простой, т.е. определение вероятностей получения конечных призов, может быть осуществлено путем расчета сумм условных вероятностей, т.е. вероятностей получения этих призов во вторичных лотереях, взвешенных по вероятностям выпадения вторичных лотерей:

p(x_i) = _i p(x_iL_j ) p( L_j).

Например, если призами в первичной лотерее выступают лотереи

L₁=(0.6, 0.4) и L₂=(0.2, 0.8), причем вероятность выигрыша L₁равна 2/3, а вероятность выигрыша L₂равна соответственно 1/3, то такая сложная лотерея будет эквивалентна простой лотерее с вероятностями получения конечных призов

(0.6 ^х (2/3) + 0.2 ^х (1/3), 0.4 ^х (2/3) + 0.8 ^х (1/3) ) = (14/30, 16/30).

Графически этот процесс сведения этой сложной лотереи к простой представлен на рис. 1.3.а, а следующий рисунок 1.3.б иллюстрирует сходную процедуру в предположении существования ( в каждой из двух вторичных лотерей ) уже не двух, а трех конечных призов.

1.3.а

1.3.б

Допустимость подобного сведения сложных лотерей к простым следует оговорить как отдельную предпосылку дальнейшего анализа (RCLA - the reduction of compound lotteries axiom), ибо с точки зрения отдельного индивида различные сложные лотереи, сводимые к одной и той же простой лотерее, могут оцениваться весьма различным образом. В частности, Джошуа Ронен (Ronen,1973) убедился, что даже простая перестановка двух этапов лотереи влияет на ее привлекательность для индивидов,а именно, семидесятипроцентный шанс получить 100 долл с вероятностью 30 % оказался более привлекательным для опрашиваемых, чем тридцатипроцентный шанс получить 100 долл с вероятностью 70 %. Но подобного рода соображения мы пока оставим в стороне, и в дальнейшем будем полагать эквивалентными различные сложные лотереи, сводимые к одной и той же простой лотерее.
Невозможность использования математического ожидания выигрыша как оценки привлекательности лотереи для индивида, т.е. ее полезности. Санкт-Петербургский парадокс

Собственно привлекательность лотереи или игры можно попытаться оценить, определив уровень ее cреднего выигрыша , стремящийся при n  к величине математического ожидания денежного выигрышаЕ(W) =

Однако еще в 18 веке такого рода подход начал вызывать серьезные возражения. В частности, Николас Бернулли в 1728 году обратил внимание на то, что ни один игрок не будет готов заплатить сколь-нибудь заметную сумму за участие в игре, математическое ожидание выигрыша в которой равно бесконечности. Суть рассмотренной им игры состояла в следующем: бросается монета, и в том случае, если орел выпадает в i - ом бросании, игрок получает выигрыш, равный2 ⁱ. Вероятность выпадения орла в i - ом бросании составляет

р_i=(1/2)ⁱ, т.е.1/2, 1/4 и т.д.

Номер игры	1	2	...	n
Выигрыш	2	4	...	2 n
Вероятность	1/2	1/4	...	1/ 2n

Е(W) == (1/2) ⁱ2 ⁱ= 1+1+.....+1= ∞

Парадоксальность этой ситуации состоит в том, что не найдется желающих платить, скажем 1 млн долл, за право участия в подобной игре, несмотря на то, что эта сумма несопоставимо меньше математического ожидания выигрыша - бесконечности.

Собственно, одновременно выдвинутая Габриэлем Крамером и Даниэлем Бернулли гипотеза о том, что важна не сама сумма выигрыша, а та полезность которую получает потребитель¹ , не является решением этого так называемого Санкт-Петербургского парадокса , но она способствовала весьма здравому теоретическому переосмыслению проблемы.

Характер предпочтения индивида относительно лотерей.

Суть этой новой концепции состояла в том, что интегральная оценка полезности лотереи должна представлять собой ту или иную комбинацию вероятностей исходов и полезностей этих исходов (а отнюдь не уровней богатства, которыми индивид обладает при различных исходах). Но построение такого рода оценки( заметим - имеющей сугубо ординалистскую природу, ведь речь идет лишь о ранжировании лотерей) предполагает наложение неких ограничений на характер предпочтений индивида на пространстве лотерей, т.е. на рассмотренном выше (n-1)-мерном симплексе .

Многое из того, что будет сказано ниже, не может не показаться знакомым, и это и неудивительно, ибо выбор между лотереями есть лишь некий частный случай общей задачи потребительского выбора. Итак, начнем с привычных аксиом потребительского выбора, лишь несколько модифицированных применительно к рассматриваемым ситуациям неопределенности.

Мы будем полагать, что предпочтения индивида на пространстве простых лотерей L асимметричны и негативно транзитивны.

Во многом мы повторим традиционные аксиомы анализа поведения потребителя , когда будем говорить о том, что

- объекты выбора(в данном случае лотереи) должны быть четко определены;

- ситуации с одними и теми же исходами должны вести к одинаковым решениям;

- индивид должен быть в состоянии произвести анализ имеющихся альтернатив;

-предпочтения относительно лотерей должны быть транзитивны, локально ненасыщаемы и т.д. и т.д.

Особое положение в перечне исходных аксиом занимает аксиома непрерывности предпочтений индивида относительно простых лотерей.

Содержательно эта предпосылка важна с той же самой точки зрения, что и в условиях определенности она позволяет упростить анализ, отказавшись от рассмотрения поведения индивидов, обладающих лексикографическими предпочтениями. Например, покупка акций, облигаций или прочих товаров, чья покупка сопряжена с той или иной степенью неопределенности, сопровождается постоянным торгом между повышением надежностью компании и понижением уровня доходности ценных бумаг. Для индивида с лексикографическими предпочтениями и приоритетом безопасности вложений над экономической выгодой такого рода решение было бы невозможно.
Теория ожидаемой полезности Неймана-Моргенштерна: линейность ожидаемой полезности в вероятностях. Теорема Неймана-Моргенштерна .

Если к числу аксиом, определяющих характер предпочтений потребителя относительно лотерей добавить еще одну - аксиому независимости, то мы тем самым перейдем к рассмотрению теории ожидаемой полезности Неймана-Моргенштерна, в соответствии с которой ожидаемая полезность представляет собой линейную комбинацию вероятностей исходов и полезностей этих исходов, т.е. сумму полезностей, получаемых индивидом при различных исходах лотереи, взвешенных по вероятностям их выпадения.

Аксиома независимости)( Samuelson,1952 ) формализует принцип некомплементарности дохода, получаемого при различных исходах (principle of nоn-complementarity of income over the states of the world) или, иными словами, независимость уровня полезности, получаемого индивидом при том или ином (например, первом, т.е. х₁ ) исходе лотереи

р о х₁ (1 - р) о х₂

от того, каким мог быть иной исход, т.е. х₂ .

Именно отказ от рассмотрения альтернатив, представляющий собой суть предпосылки независимости, и позволяет строить функцию кардиналистской полезности(иначе называемую функцией Бернулли), ставящую в соответствие каждому призу(выигрышу) некий уровень полезности, определяемый лишь размерами полученного приза.

	х1 ,	х2 ,	.... ,	хn
	u(х1),	u(х2),	.... ,	u(хn)

Итак, речь идет о независимости кардиналистcкой полезности от контекста, в котором индивид сталкивается с исходом х_i. Разумеется, измеряя полезность исходов u(х_i) в неких малопонятных "ютилах", следует допустить неединственность этого измерителя. В данном случае допустимыми будут лишь аффинные преобразования функции Бернулли а + bu, b ≠ 0, сохраняющие относительное "расстояние" между полезностью различных исходов, что, в конечном итоге, обеспечивает сохранение прежнего ранжирования лотерей.

Итак, в условиях заданности альтернативного исхода (х₂) и вероятности его выпадения (1 - р) ранжирование лотерей, различающихся лишь первым исходом (х₁) , определяется порядком ранжирования этих исходов. Предположим, индивид может подвергнуться нападению в ходе путешествия. Причем вероятность этого нападения не зависит от того, каким видом транспорта он предпочтет воспользоваться. В свете принятой предпосылки при равной вероятности подвергнуться нападению выбор индивида будет обусловлен сравнительными преимуществами отдельных видов транспорта.

Суть дела не меняется, если в качестве исходов первичной лотереи выступают некие вторичные лотереи. Предположим, что речь идет о сложной лотерее, в которой с вероятностью (1 - а) можно выиграть лотерею L₃ , а с вероятностью а оказаться вновь перед выбором между лотереей L₁ и лотереей L₂ .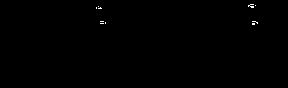



Принятие аксиомы независимости обусловливает выбор между сложными лотереями

а о L₁ (1 - а) о L₃ и а о L₂  (1 - а) о L₃

выбором между L₁ и L₂ :

L₁ L₂  а о L₁ (1 - а) о L₃ > а о L₂  (1 - а) о L₃

L₁ L₂ а о L₁ (1 - а) о L₃ а о L₂  (1 - а) о L₃

Иначе говоря, при изолированном "смешении " исходных простых лотерей L₁ и L₂ с третьей лотерей L₃ в определенной "пропорции", задаваемой вероятностью а , порядок ранжирования этих "смесей" соответствует порядку ранжирования исходных лотерей, и не зависит от того, что собой представляет эта третья лотерея. В противном случае - если бы характер лотереи L₃ влиял бы на порядок ранжирования "смешанных" лотерей, то можно было бы говорить о существовании комплементарного эффекта.

Следует отдавать себе отчет в том, что принятие подобной предпосылки является ограничивающим, и это действительно так. Но все же не до такой степени, как это было бы, если бы некий исход лотерей L₁ или L₂ сопровождался бы неким исходом другой лотереи, т.е. L₃ . Обратите внимание- речь идет о взаимоисключающих лотереях (на первом этапе индивид получает либо L₁ или L₂ , либо L₃ ).

Теорема Неймана-Моргенштерна:

Если выполняются ранее изложенные предпосылки, то существует функция полезности, удовлетворяющая свойству ожидаемой полезности: U(L) = Eu(L) =i pi u(xi ) и L1 L2 тогда и только тогда, когда Eu (L1) ≥ Eu (L2 ), т.е. 

Итак, общем виде ожидаемая полезность может быть определена как модель, предсказывающая или предписывающая максимизацию индивидом взвешенной по вероятностям суммы полезностей отдельных исходов: ,

где w_i - возможный выигрыш

р( w_i ) - вероятность этого выигрыша.

Означает значит ли использование кардиналистских функций полезности u(w_i), что теория Неймана-Моргенштерна является кардиналистской? С точки зрения измерения полезности - да, безусловно, но с точки зрения предпочтений ее " следует трактовать как ординалистскую , поскольку она обеспечивает лишь порядковое ранжирование лотерей. Поэтому полезность по Нейману-Моргенштерну не следует интерпретировать как измерение силы предпочтения в условиях определенности, что качественно отличает ее от неоклассической кардиналистской полезности. Это объясняется тем, что предпочтения, придаваемые лотереям определяются по крайней мере двумя различными факторами, а именно:

1) силой предпочтений достоверных исходов;

2) отношением к риску.

Функция Неймана-Моргенштерна является составной комбинацией этих двух факторов, которая не требует ни прямого сопоставления интервалов, ни измерения силы предпочтений. Как теория предпочтений она является всецело ординалистской. Тем не менее она неявно предполагает, что существует полезность неоклассического типа - иначе было бы невозможно определить достоверный эквивалент лотерей"¹

Ожидаемая полезность по Нейману-Моргенштерну линейна по вероятностям, и , соответственно, кривые безразличия функции ожидаемой полезности на (n -1)-мерном симплексе будут линейны и параллельны друг другу (рис.1.4.а. и рис.1.4.б.):

U(L) = Еu== const .

Однако для их рассмотрения будет удобнее воспользоваться не традиционным симплексом, а так называемым треугольником Маршака- Машина( the Marschak-Machina triangle)(см. рис. 1.4.в)

Перейти к нему возможно, выразив вероятность второго исхода через вероятности первого и третьего исхода:

U(L) = Eu == const ; =1

p3 = const + [(u2 -u1)/(u3 –u2)]p1

Тем самым кривые безразличия, изображенные в осях (p₁,p₃)

• при u₁ < u₂ <u₃ будут иметь положительный наклон ;

• представляют собой прямые линии, т.к. выражение для p₃ линейно относительно p₁;

• более того - параллельны друг другу, т.к. отношение (u₂ -u₁)/(u₃ -u₂) представляет собой некую константу.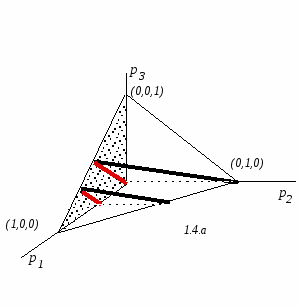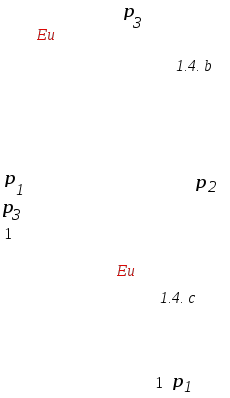



Теория ожидаемой полезности, в условиях, когда поведение индивида соответствует аксиомам, представляет собой весьма полезный инструмент для принятия решений в условиях неопределенности. В частности, она позволяет решить проблему выбора в ситуации, когда различия в вероятностях получения призов слишком малы, и вследствие этого не могут быть оценены индивидом.

Рассмотрим две лотереи L₁ и L₂ , близко расположенные друг к другу в треугольнике Маршака - Машина.

Рис.1.5.а

Рис.1.5.б

В подобном случае уместно вспомнить о свойствах ожидаемой полезности по Н.- М., а именно, о ее линейности по вероятностям. Решая конкретную проблему о выборе одной из двух близких лотерей, следует сравнить между собой лотерею L₁ и лотерею L₃ , которой будет соответствовать точка, лежащая на продолжении прямой линии, соединяющей точки L₁ и L₂ , на некотором отдалении, достаточном для однозначного ранжирования точек L₁ и L₃ . В том случае, если L₃ L₁ , можно утверждать, что и L₂ L₁ , и , наоборот, выполнение условия L₁ L₃ должно означать, что L₁ L₂ .

Иначе говоря, усугубив различия между точками, можно сделать вывод о направлении возрастания уровня полезности вдоль линии, соединяющей две исходные точки.

Линейность ожидаемой полезности в вероятностях как тестируемая гипотеза. Отмеченные нарушения линейности.

Традиционно перечень экспериментальных свидетельств, ставящих под сомнение гипотезу максимизации ожидаемой полезности по Нейману-Моргенштерну, начинается описанием парадокса Алле, датируемым еще 1952 годом. Однако мы попытаемся несколько сократить изложение, обратив внимание на общие черты экспериментов, нацеленных на проверку гипотезы линейности ожидаемой полезности в вероятностях.

Типичным в подавляющем большинстве подобных экспериментов являлось то, что респондентам предлагалось провести попарное сопоставление четырех лотерей: А₁, А₂, B₁, В₂ . Лотереи преднамеренно подбирались таким образом, чтобы линии А₁А₂ и B₁В₂ , соединяющие точки в треугольнике Маршака-Машина, и соответствующие каждой паре лотерей, были параллельны друг другу. Результат выбора, сделанного индивидом в первой паре лотерей: А₁ или А₂, сопоставлялся с результатом выбора во второй паре лотерей: В₁ и В₂. Возможные сочетания : А₁В₁(т.е. А₁ - в первой паре и В₁ - во второй), А₁В₂, А₂ В₁ и А₂ В₂ .

Какие ограничения накладывает на поведение индивида аксиома независимости, т.е. линейность ожидаемой полезности по вероятностям?Как уже говорилось, кривые безразличия функции ожидаемой полезности по Нейману-Моргенштерну в треугольнике Маршака-Машина должны представлять собой параллельные прямые линии с положительным(при возрастании призов по мере увеличения индекса) наклоном. Соответственно, в том случае, если линии, соединяющие лотереи, входящие в каждую пару : А₁А₂и B₁ В₂ , также параллельны друг другу, выбор А₁В₂ и А₂ В₁ будет противоречить гипотезе ожидаемой полезности. При попарном сравнении лотерей( А₁ - А₂и B₁ - В₂ ), лежащих на паралельных линиях А₁А₂и B₁ В₂ , избираться всегда должны лотереи, соответствующие не диагональным элементам, а одной стороне четырехугольника. В случае, иллюстрируемом рис.1.6.а подобный выбор соответствует А₁ B₁ , а в случае, иллюстрируемом рис.1.6.б: А₂ B₂ . Различие между двумя этими вариантами обусловлено лишь тем, как соотносится наклон кривых безразличия функции ожидаемой полезности и кривых А₁А₂и B₁ В₂ ( в первом случае наклон кривых безразличия - более крутой, а во втором - более пологий, чем наклон кривых А₁А₂и B₁ В₂ .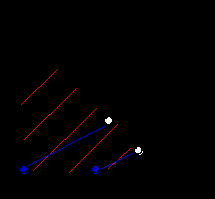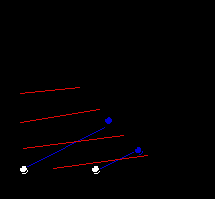

Рис.1.6.а А1В1

Рис.1.6.б А2В2

Рассмотрим вначале следующий пример:

Лотереи	х1 = 0	х2 = $ 3 тыс	х3 = $ 4 тыс
А1	0	 1	0
А2	0.2	0	0.8
В1	0.75	0.25	0
В2	0.8	0	0.2

Тангенс угла наклона кривой А₁ А₂. = 0.8/0.2 = 4

Тангенс угла наклона кривой B₁ B₂. = 0.2/( 0.8 - 0.75)= 0.2/ 0.05 = 4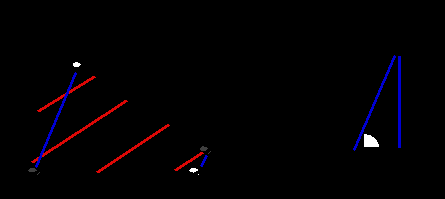

рис. 1.7.а

При попарном сравнении подавляющее большинство опрашиваемых полагали А₁ А_{2 ,}и в то же самое время многие из них предпочитали лотерею В₂ лотерее В₁ , хотя принятие аксиомы независимости и соответствующая линейность ожидаемой полезности в вероятностях диктуют иной выбор, а именно В₁ В₂ (коль скоро А₁ А₂ )

В₁ 0.75 о $ 0 0.25 о А₁ В₂ 0.75о $ 0 0.25 о А₂



Этот эксперимент представляет собой непосредственную проверку того, соответствует ли поведение индивидов аксиоме независимости. Возможно некоторое его усложнение, в котором лотерея L^* предполагает гарантированное получение некоторого выигрыша х_2, а лотерея L^** - получение c некоторыми вероятностями призов х₁ и х₃, таких, что х₁ < х₂<х_{3 .} При этом



Как уже говорилось, линейность ожидаемой полезности при попарном сравнении диктует выбор либо А₁В₁ , в том случае, если L^* предпочтительнее L^**, либо А₂ В₂ - в противном случае, но в подавляющем большинстве опрашиваемые и в этом случае выбирали A₁В₂ , демонстрируя модель поведения, несовместную с ограничениями на вид кривых безразличия, накладываемыми аксиомой независимости.

Полученный результатсвидетельствует о либо о неполноте предпочтений( и тогда анализ утрачивает всякий смысл), либо о том, что кривые безразличия не являются прямыми параллельными линиями с положительным наклоном, как это предполагается теорией ожидаемой полезности Неймана-Моргенштерна.

Известный парадокс Алле, несмотря на то, что он был выдвинут вне более общего контекста, представляет собой, по сути, частный случай ранее рассмотренного примера. Различие состоит в том, что четырехугольник А₁А₂ В₂ В₁ в парадоксе Алле представляет собой параллелограмм , в то время как прежде он имел вид трапеции. Большой роли это не играет: важна лишь параллельность сторон А₁А₂и B₁ В₂ .

Парадокс Алле(Allais Paradox,1952)

Попарно сопоставляется привлекательность лотерей А₁, А₂, В₁, В₂ , разнящиxся вероятностями получения трех различных денежных выигрышей: $ 0, $ 1 млн и $ 5 млн

Лотереи	Х1 = $ 0	х2 = $ 1 млн	х3 = $ 5 млн
А1	0	1	0
А2	0, 01	0, 89	0,10
В1	0, 89	0,11	0
В2	0, 9	0	0,10

Особенность условий эксперимента, как уже отмечалось, состоит в том, что точки, соответствующие лотереям , будучи соединены прямыми линиями, образуют параллелограмм А₁А₂ В₂ В₁ (рис. 1.7.а).

рис. 1.8.а

рис. 1.8.б

Как выяснилось в результате проведенных экспериментов, опрашиваемые индивиды при попарном сравнении, как правило, выбирают «диагональные» лотереи, в частности, предпочитают лотерею А₁ лотерее А₂ и лотерею В₂ - лотерее В₁ :

А₁ А₂ и В₂ В₁ ,

что противоречит гипотезе о линейности ожидаемой полезности по вероятностям. (рис1.8.б.).

Эффекты контекста или рамочные эффекты (framing effects)

1. Slovic(1969) и Payne &Braunstein(1971) проводили серию опросов предпочтительности для индивидов различных вариантов так называемых дуплексных игр( duplex games).

Предположим, перед индивидом крутятся два барабана. Первый барабан(барабан выигрышей) с некоторой вероятностью указывает на выигрыш $ 0.4 или нулевой выигрыш. Второй(барабан проигрышей) - с некоторой вероятностью указывает на проигрыш $ 0.4 или нулевой выигрыш. В итоге индивид получает разность выигрыша и проигрыша.

Индивидам были предложены два варианта игры: А и В.

В игре А

вероятность выигрыша $ 0.4 (на первом барабане) составляла 60 %,

а вероятность проигрыша $ 0.4 на втором барабане была равна 50 %.

В игре В

вероятность выигрыша $ 0.4 (на первом барабане) составляла 50 %,

а вероятность проигрыша $ 0.4 на втором барабане была равна 40 %.

Обозначим выигрыши w =(w₁, w₂ ,w₃ )=( 0.4, - 0.4, 0)

Несложно убедиться, что обе эти игры сводимы к одной и той же простой лотерее

L = (0.3, 0.2, 0.5),

но индивиды систематически выбирали игру А.

2). Точка отсчета ( reference point)

Обратите внимание: исходы лотерей тождественны, различаются лишь их описания

.• первый вариант (Kahneman & Tversky(1979)

Индивиду дают $ 1000 и предлагают на выбор

А₁ 1 о $ 500 84%

_А2 0.5о $ 1000  0.5о $ 0

Индивиду дают $ 2000 и предлагают на выбор

В₁ 1 о (- $ 500)

В₂ 0.5о (- $ 1000)  0.5о $ 0 69%

• второй вариант Kahneman & Tversky(1981)

600 человек может умереть в результате некоей болезни.

Возможно два варианта действий

А₁ 200 чел будет спасено выбрали 72%

_А2 1/3 о (600 чел будет спасено) 2/3 о 0 (никто не будет спасен)
В₁ 400 чел умрет

В₂ 1/3о (никто не умрет)  2/3о (600 умрут) выбрали 78%
3. Парадокс Эллсберга(Ellsberg)

Индивиду предлагается выбрать одну из двух урн, содержащих по 100 шаров красного и черного цвета. В первой урне содержится одинаковое количество красных и черных шаров, содержание второй урны неизвествно. В соответствии с условиями игры, индивид, вытянувший красный шар, получает $ 100. Большинство респондентов выбрали первую урну, что, кстати, не помешало им вновь выбрать эту же урну, при изменении условий игры, а именно, при обещании выдавать ту же сумму при вытягивании не красного, а черного шара.