1 Неопред БИ 12. 1. Неопределенность информации

• Название: 1. Неопределенность информации
• Дата: 19.09.2018
• Размер: 1.17 Mb.
• Имя файла: 1 Неопред БИ 12.doc
• Тип: Документы; #51096
• страница: 2 из 6

Риск и отношение к риску. Меры несклонности к риску.

Измерение степени риска(степени рискованности игры). Стохастическое доминирование первого и второго рода.
Стохастическое доминирование первого рода.

Рассмотрим два распределения F(W) и G(W)(см. рис(2.1.а).

С одной стороны, с некоей заданной вероятностью можно получить выигрыш

W ≤ w_F - при распределении F и W ≤ w_G- при распределении G . Т.к. F(W ) ≤ G(W ) для любогоW, то, следовательно, w_F >w_G, что позволяет оценивать распределение F как менее рискованное. Иначе, более корректно, эту мысль можно сформулировать, указав на стохастическое доминирование распределения F распределения G.

Def. Распределение F(W) первично стохастически доминирует распределение G(W) (F(W) first-order stochastically dominates G(W)), тогда и только тогда, когда F(W ) ≤ G(W) для любогоW.

Рис.2.1.а Доминирование первого рода

Соответственно, если распределение F первично стохастически доминирует распределение G, то

• при распределении выигрышей F математическое ожидание выигрыша будет выше чем при распределении G:

W dF(W) ≥ W dG(W)

Графически это может интерпретироваться следующим образом(простоты ради зададим в данном случае совпадающие интервалы выигрышей):

Рис.2.2.а E(W) =W dG(W)

Рис.2.2..б E(W) = W dF(W)

Рис.2.2..в E(W) =  W dF - W dG

•при распределении выигрышей F ожидаемая полезность будет выше, чем при распределении G, т.е. для любой неубывающей функции u(W) выполняется условие

Eu (F ) ≥ Eu (G ) u(W) dF(W) ≥ u (W) dG(W ).

Обратите внимание, на то обстоятельство, что несмотря на то, что стохастическое доминирование первого рода позволяет нам проранжировать лотереи как по уровню матетамического ожидания выигрыша, так и по уровню их ожидаемой полезности, обратное неверно, т.е. ни по уровню математического ожидания выигрыша , ни по уровню ожидаемой полезности нельзя делать вывод о стохастическом доминировании первого рода, поскольку ранжирование лотерей с точки зрения доминирования первого рода является частичным. Например, распределение G(W ) первично стохастически доминируется распределениями F(W) и F '(W), но не существует возможности, рассматривая лишь доминирование первого рода, проранжировать эти два последние распределения.

Рис.2.3.

Стохастическое доминирование второго рода при совпадении математического ожидания выигрышей.

Несколько упрощая рассмотрение стохастического доминирования второго рода, сконцентрируемся лишь на тех распределениях, которые характеризуются совпадением математических ожиданий выигрышей.

Итак, две игры могут иметь одно и тоже математическое ожидание выигрыша, но различаться в степени своей рискованности. Например, игра, в которой с вероятностью 1/2 можно выиграть и с вероятностью 1/2 проиграть h долларов всегда будет менее рискованной чем игра, где с равными вероятностями можно выиграть или проиграть 2 h долларов. В подобном случае уместно говорить о стохастическом доминировании второго рода или вторичном стохастическом доминировании.

Def. Распределение F(W) вторично стохастически доминирует

распределение G(W) ( F(W) second-order stochastically dominates G (W) ),

имеющее такое же математическое ожидание

 W dF(W) =  W dG(W),

если распределение G предполагает больший разброс выигрышей, т.е. его дисперсия больше.

Пример. Сравним две игры, имеющие распределение G(W) и F(W) .В первой игре с вероятностями 0.25 можно выиграть 1, 2, 3 и 4. Во второй с вероятностями 0.5 можно получить 2 и 3. В обоих случаях математическое ожидание одинаково - 2.5 , что графически иллюстрируется совпадением площадей заштрихованных фигур.

Но поскольку в распределении G(W) задан больший разброс выигрышей, т.е. его дисперсия выше, чем при распределении F(W), оно является более рискованным.

Рис.2.4.а

Рис.2.4..б

Рис.2.4.в

Без доказательства приведем теорему, гласящую, что, если распределение F(W) вторично стохастически доминирует распределение G(W), то для любой возрастающей вогнутой функции полезности u(W) выполняется условие

 u(W) dF(W) ≥  u(W) dG(W).

Обратите внимание на то, что в данном случае мы формулируем этот вывод лишь для вогнутых, т.е. свидетельствующих о несклонности индивида к риску, кардиналистских функций полезности u(W), в то время как говоря о сходном результате, связанном со стохастическом доминированием первого рода, мы оговаривали лишь неубывающий характер этой функции . Несколько позже этот результат может быть легко получен и графически проиллюстрирован. Проделайте это в качестве упражнения(после прочтения всей темы).
Отношение к риску: склонность, несклонность(неприятие) и нейтральность. Критерии оценки отношения индивида к риску.

Попадая в одни и те же рискованные ситуации, индивиды демонстрируют тем не менее весьма различные стратегии поведения. Следовательно, наряду с различиями в степени рискованности лотерей внимания заслуживают и различия в отношении различных индивидов к риску . Самая общая классификация предполагает деление экономических агентов на три основные группы : не склонные, склонные и нейтральные к риску.

• Индивид, не склонный к риску, всегда предпочтет участию в игре гарантированное получение суммы, соответствующей математическому ожиданию выигрыша:

u(E(W)) > Eu .

• Индивид, склонный к риску, всегда предпочтет участие в игре гарантированному получению суммы, соответствующей математическому ожиданию выигрыша:

u(E(W)) < Eu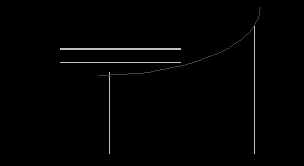

Рис.2.5. а Индивид не склонен к риску( is globally risk-averse). Функция полезности вогнутая: < 0

Рис.2.5.б Индивид склонен к риску( is globally risk-lover). Функция полезности выпуклая: > 0

• Нейтральность к риску (risk-neutrality), т.е. безразличие между участием в справедливой игре и гарантированным получением суммы, соответствующей математическому ожиданию выигрыша: u(E(W)) = Eu ,предполагает линейность функции Бернулли : u(W) = a + bW, u "(W) = 0

Рис.2.5.в Индивид нейтрален к риску( is globally risk-neutral). Функция полезности линейна: = 0

Итак:

несклонность к риску	u '(W) > 0; u "(W) < 0	u(W) вогнутая
склонность к риску	u '(W) > 0; u "(W) > 0	u(W) выпуклая
нейтральность к риску	u '(W) > 0; u "(W) = 0	u(W) линейнaя

Несложно догадаться, что характер функции u(W), т.е. ее вогнутость, либо выпуклость, не может не сказаться и на виде кривых безразличия функции ожидаемой полезности. И это действительно так, в чем можно убедиться перейдя, в частности, к рассмотрению уже упоминавшегося треугольника Маршака- Мaшина( the Marschak-Machina triangle).

Наряду с кривыми безразличия, т.е. прямыми линиями, соответствующими заданному уровню ожидаемой полезности, изобразим в треугольникеМаршака- Машина и так называемые линии постоянного ожидаемого выигрыша (iso-expected value lines), представляющие собой совокупность точек, соответствующих лотереям с одинаковым математическим ожиданием выигрыша:

= const ; =1p₃= const + [] p₁

Полученное выражениесвидетельствует о том, что линии постоянного ожидаемого выигрыша (также как и кривые безразличия) будут параллельными прямыми линиями, имеющими положительный наклон приw₁ < w₂ <w₃ .

Именно соотношение наклонов кривых безразличия и кривых постоянного ожидаемого выигрыша, и будет характеризовать отношение индивида к риску.

Рассмотрим два треугольника Маршака- Машина , на которых пунктиром обозначены линии постоянного ожидаемого выигрыша( iso-expected value lines), а непрерывными линиями - кривые безразличия.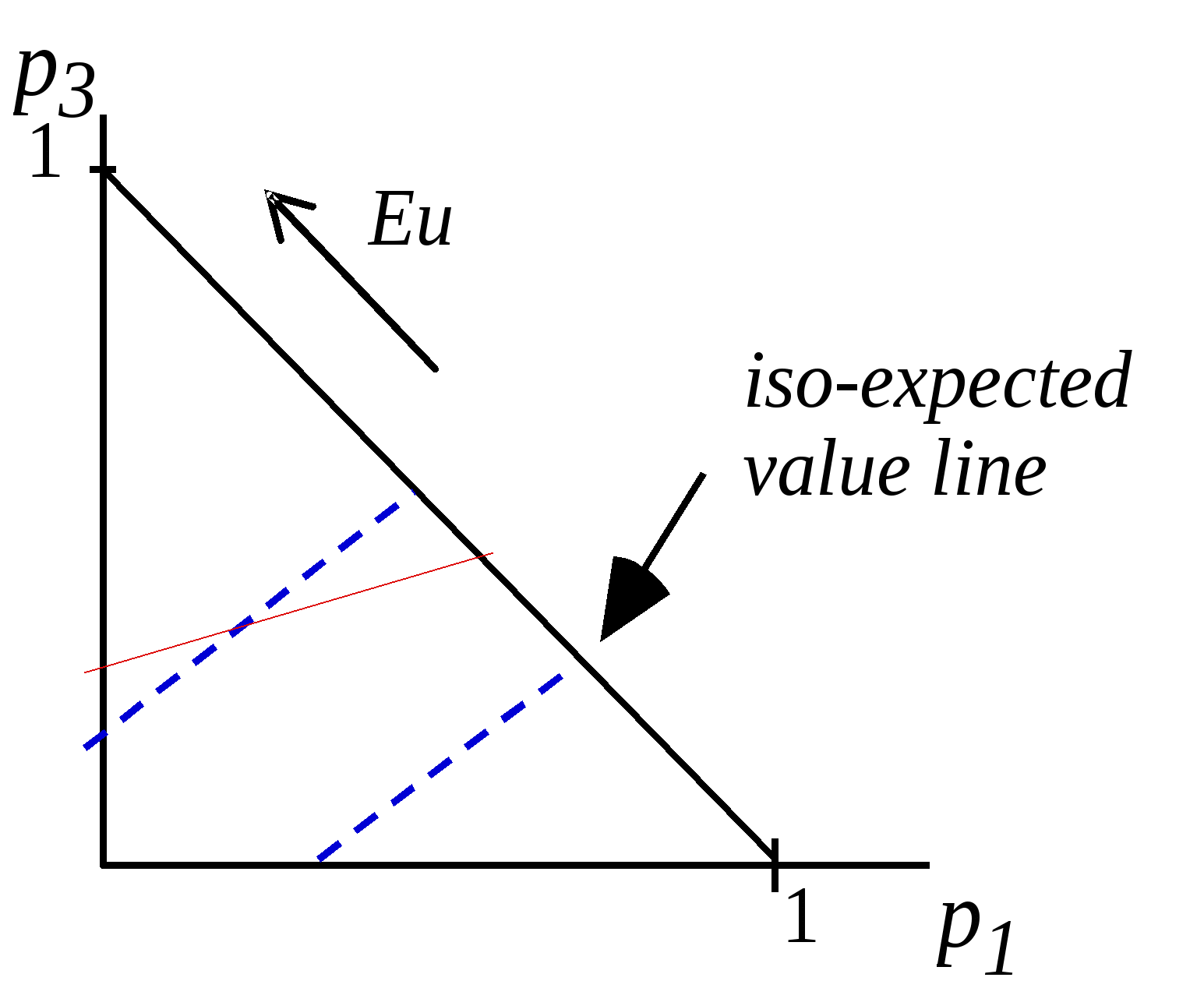

Рис.2.6.а Индивид не склонен к риску.

Рис.2.6.б Индивид склонен к риску.

Cдвигу вдоль линий постоянного ожидаемого выигрыша к северо- востоку, соответствует повышение степени рискованности лотереи - при том же математическом ожидании выигрыша сокращается вероятность выигрыша промежуточного приза(w₂) при росте вероятностей выигрыша большего(w₃) и меньшего (w₁) призов. Уместно предположить, что для индивида, не склоненного к риску, подобного рода перемещение в треугольнике Маршака-Машина должно сопровождаться сокращением уровня получаемой им полезности, и, соответственно, его кривые безразличия имеют более крутой наклон, чем линии постоянного ожидаемого выигрыша(Рис.2.6.а ).

В противном случае, когда кривые безразличия являются более пологими, чем линии постоянного ожидаемого выигрыша , индивид отчетливо демонстрирует склонность к риску(Рис.2.6.б ). Нейтральность к риску предполагает совпадение углов наклона кривых постоянного ожидаемого выигрыша и кривых безразличия.

Иначе отношение индивида к риску скажется на кривых безразличия, изображаемых на пространстве условных благ. Набору условных благ соответствует точка, координаты которой характеризуют уровни благосостояния в различных состояниях(Wg иW_b будут соответствовать "богатству" в хорошие и плохие времена).

Для индивидов, не склонных к риску, кривые безразличия функции ожидаемой полезности кривые Eu = u(W₁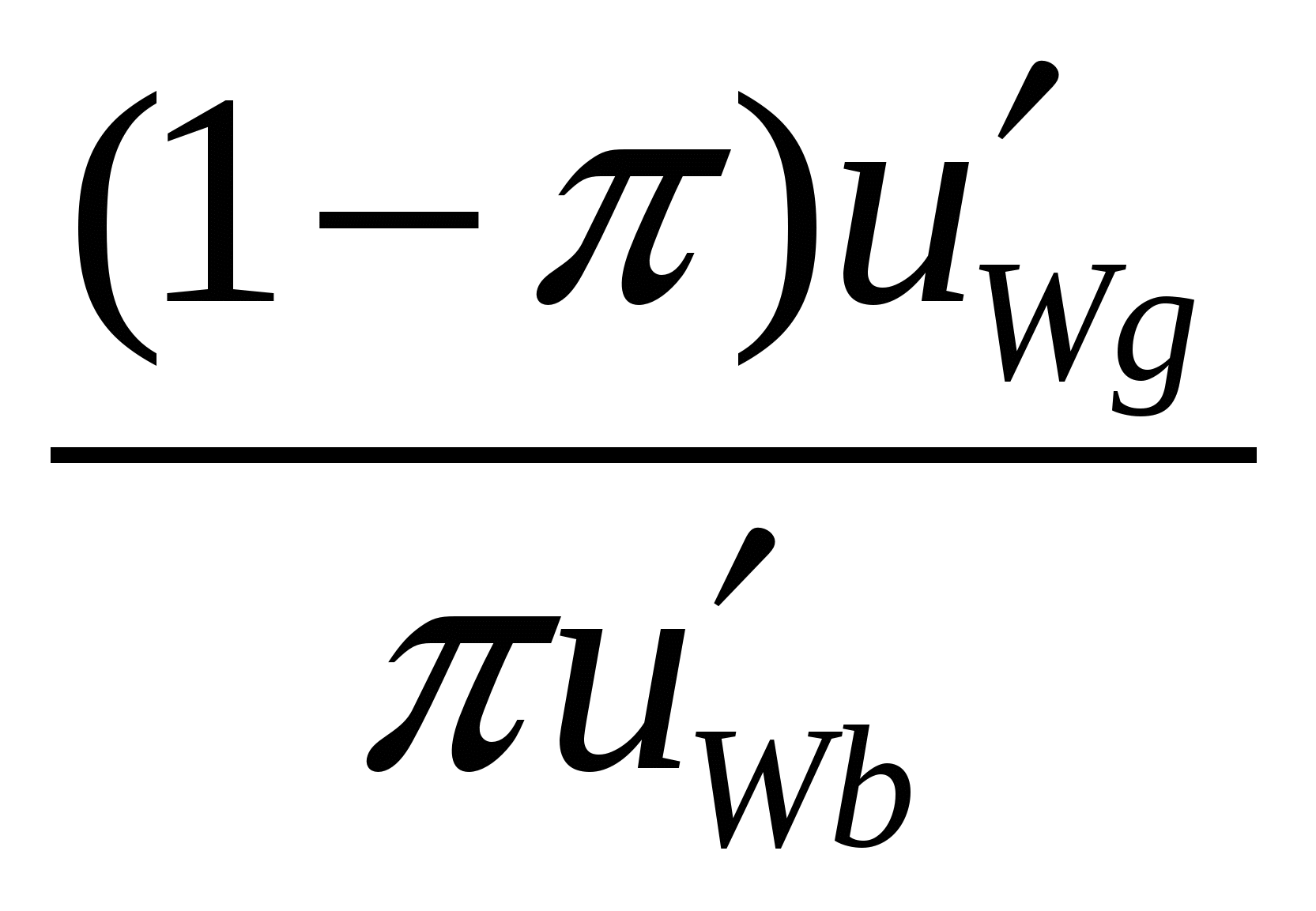)+(1 - )u(W₂) будут иметь традиционный (выпуклый) вид, поскольку при увеличении потребления условного блага Wg значения предельной нормы замещения

MRS= =

будут убывать. В сущности, можно было ограничиться указанием на то, что функция ожидаемой полезности, представляющая собой выпуклую комбинацию вогнутых функций, также должна обладать свойством вогнутости, а , следовательно - и квазивогнутости, что, в свою очередь, предполагает убывание предельной нормы замещения. Иначе тот же результат можно получить, взяв производную MRS по W_g (это выражение неоднократно будет использовано впоследствии):

= [ (1-) / u'(W_b)²] {[u''(W_g)u'(W_b)] -[u'(W_g)u''(W_b)(dW_b/dW_g)] }

Заметим, что знак этой производной будет определяться знаком выражения в фигурных скобках (первый сомножитель заведомо положителен), а он( ввиду вогнутости функции Бернулли: u''(W)< 0)будет негативным.

Нейтральность к риску предполагает линейность кривых безразличия и совпадение резервной кривой безразличия с кривой постоянного ожидаемого выигрыша:

MRS ==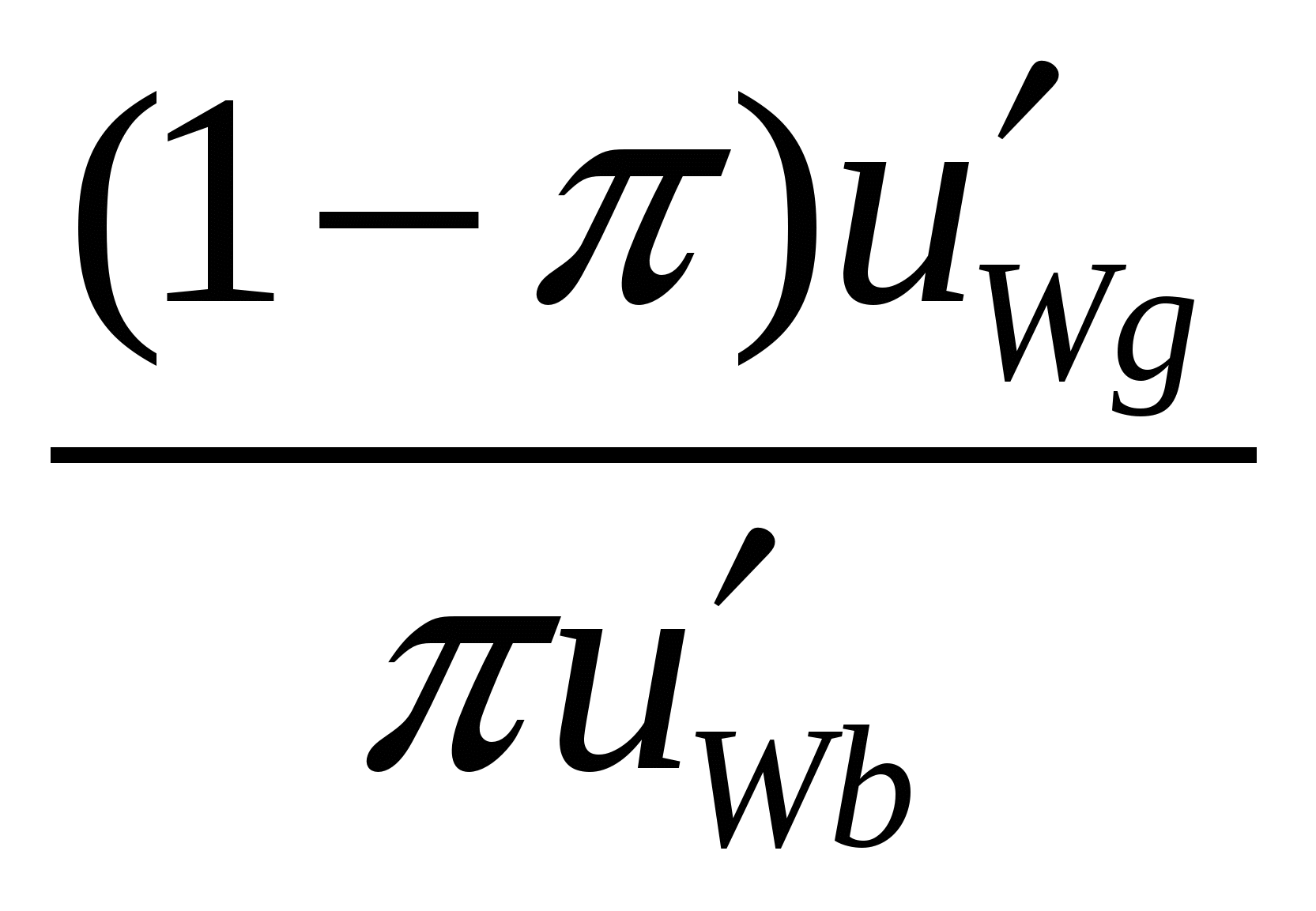

а склонность к риску графически будет иллюстрироваться кривыми безразличия, при движении вдоль которых MRS будет возрастать: при увеличении Wg числитель дроби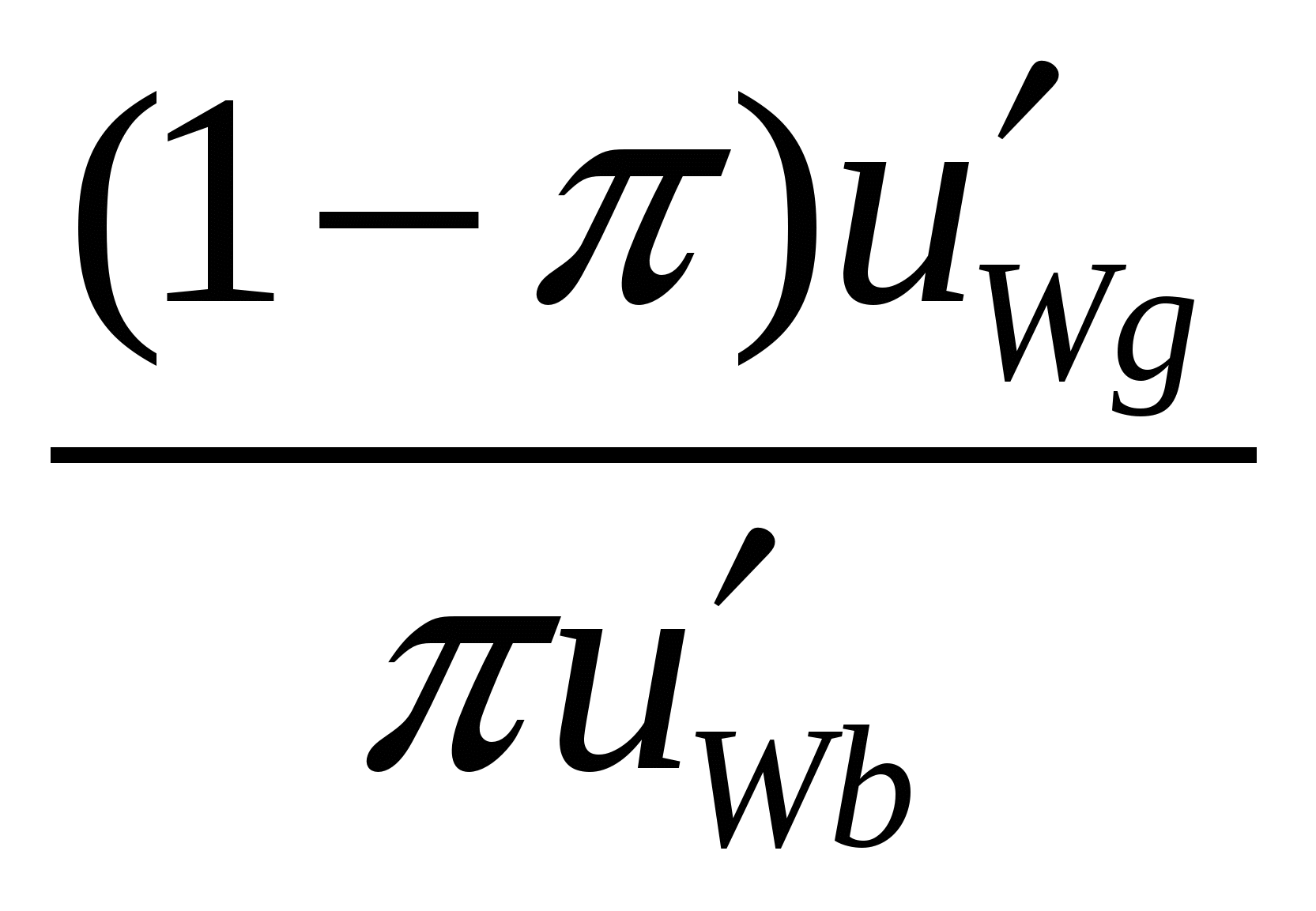

будет возрастать одновременно с убыванием знаменателя.

Рис.2.7.а Несклонность к риску.

Рис.2.7.б Нейтральность к риску.

Рис.2.7.в Склонность к риску.

Обычно полагается, что индивид не склонен к риску. Подтверждением тому служит, в частности, стремление индивида дивеpсифицировать свой портфель. Действительно, нейтральный к риску индивид стремился бы вложить свои сбережения в ценные бумаги, обеспечивающие максимальное математическое ожидание дохода, в то время как диверсификация портфеля, гарантирующая индивида от провально низких уровней дохода за счет потери части ожидаемого дохода, является своего рода страховой премией, уплачиваемой не склонным к риску индивидом.

Тем не менее в определенных ситуациях люди демонстрируют поведение совершенно иного типа. Те же самые индивиды, которые проявляют свою несклонность к риску, страхуя здоровье и имущество, наполняют залы казино, являющихся, казалось бы, естественным местом обитания любящих риск индивидов. Объяснением тому может служит указание на то обстоятельство, что для большинства людей игра в рулетку - это скорее отдых, чем деятельность, нацеленная на повышение дохода, соответственно, проигранные деньги возможно списать на приобретение потребительских ценностей.Это скорее consumption good, чем investment good.

О том, что индивиды отнюдь не всегда несклонны к риску свидетельствуют и приведенные ранее в связи с рамочным эффектом примеры. Один из них, приведенный в работе Kahneman & Tversky "Prospect theory: an analysis of decision under risk" (Econometrica, 1979) выглядит следующим образом:

AИндивиду дают $ 1000 и предлагают на выбор

А₁ 1 о $ 500 84%

_А2 0.5о $ 1000  0.5о $ 0

BИндивиду дают $ 2000 и предлагают на выбор

В₁ 1 о (- $ 500)

В₂ 0.5 о (- $ 1000) 0.5 о $ 0 69%

В лотерее А 84% респондентов выбрали гарантированное получение $ 500 , демонстрируя явную несклонность к риску, и в тоже время в игре B 69% респондентов предпочли вторую лотерею, т.е. модель поведения, присущую любящим риск.

Kahneman & Tversky объяснили подобный асимметричный результат уже упомянутым выше"рамочным эфектом", состоящим в том, что индивиды демонстрируют несклонность к риску при формулировании этих тождественных ситуаций в терминах приобретения, но склонны к риску, когда речь идет о потерях.


Рис.2.8

Впрочем, следует подчеркнуть, что само по себе желание застраховаться или заплатить за участие в игре может служить индикатором склонности или несклонности к риску только в том случае, если речь идет о справедливых играх. Несложно привести примеры неблагоприятных игр, непривлекательных и для индивидов любящих риск или же примеры благоприятных игр, за участие к которых готовы будут заплатить и не склонные к риску агенты. Впрочем, для того, чтобы подробнее разобраться в этом вопросе, следует ввести понятия достоверного эквивалента, рисковой премии, справедливой премии и пр.
Достоверный эквивалент. Рисковая премия. Справедливая(fair) премия. Вероятностная премия

Достоверным эквивалентом (certainty equivalent) (c) называется денежная сумма, гарантированное получение которой с точки зрения индивида будет равноценно участию в игре:

U [ о W₁ (1-)о W₂] = Eu = u(W₁)+(1 - )u(W₂) = u(c)

Определение достоверного эквивалента с, задаваемого посредством функций распределения:

U = Eu =u (W) dF(W ) = u [с(F,u )]

Рис.2.9

Собственно, именно величина достоверного эквивалента и представляет собой минимальную цену, по которой индивид будет готов продать право участия в игре или же - максимальную цену, по которой он готов будет его купить.

Как уже отмечалось, u (W), называемая кардиналистской функцией полезности или функцией Бернулли, часто трактуется ( в полном соответствии с подходом Бернулли) как кардиналистская полезность в условиях определенности, т.е. как полезность при гарантированном получении некоторой суммы денег W.

Но этот подход не является единственно возможным. В частности, Пол Шумейкер настаивает на необходимости иного подхода к интерпретации u (W), рассматривая ее как кардиналистскую меру полезности достоверного эквивалента лотереи, т.е. как кардиналисткую полезность в условиях неопределенности).

Рисковая премия (risk premium), обозначаемая в дальнейшем r, представляет собой максимальную плату, которую не склонный к риску индивид готов заплатить за то, чтобы избавиться от предстоящей ему справедливой игры, и , соответственно, равна разности между математическим ожиданием выигрыша E(W) и величиной достоверного эквивалента игры (c):

r = E(W) - c

Рис.2.10 Рисковая премия ( risk premium) r = E(W) - c.

Рассмотрение неблагоприятной игры предполагает некоторое усложнение. А именно, наряду с введением понятия рисковая премия оно требует также введения понятия справедливая премия ( а fair premium).

Справедливая премия ( а fair premium) , обозначаемая в дальнейшем r ^*, представляет собой разность между суммой, которой индивид обладал первоначально, и математическим ожиданием выигрыша:

r^* = W₀ - E(W)

Рис.2.11 Справедливая премия в неблагоприятной ( W0 =W2) игре : r* = W0 - EW > 0

После уплаты или напротив - получения индивидом справедливой премии(все зависит от уровня его первоначального богатства ), игра для него перестает быть несправедливой и превращается в справедливую. Действительно, перед ее началом индивид обладает суммой денег, равной математическому ожиданию выигрыша). Справедливая премия тем самым может интерпретироваться как (до)плата за превращение игры из неблагоприятной в справедливую .

Именно на величину r^*максимальная сумма денег, которой индивид будет готов пожертвовать, с тем чтобы избежать участия в неблагоприятной игре, т.е. (W₀ - c),будет превышать размер рисковой премии r :

r^*+ r = [W₀ - E(W)]+ [ E(W)- c]= W₀ - c

• Для несклонного к риску индивида, чьи предпочтения будут выпуклыми,

графически проиллюстрируем введенные понятия на пространстве условных благ. Проведем из начала кординат луч, имеющий наклон 45 градусов. Подобного рода линию в дальнейшем мы будем называть линией уверенности (certainty line), поскольку для любой ее точки выполняется условие Wg= W_b

Через исходную точку ( W₂ ,W₁) также следует провести резервную кривую безразличия , т.е. кривую безразличия, соответствующую уровню ожидаемой полезности, получаемой незастрахованным индивидом:

Eu ^R = Eu = u(W₁)+(1 - )u(W₂)

Эта кривая безразличия пройдет через точки (W_b, W_g), такие что

Eu =u (W_b