1 Неопред БИ 12. 1. Неопределенность информации
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
) + (1- и пересечет линию уверенности в некоторой точке координаты которой( равные по обеим осям) будут равны достоверному эквиваленту лотереи c.  Рис.2.12. Рис.2.12.Следующим шагом будет построение линии математического ожидания выигрыша ( iso-expected value linе) незастрахованного индивида E W = Наклон этой линии будет равен - (1 - E(W) = Wb = соnst - Сдвигаясь по этой линии вверх вплоть до точки ее пересечения с линией уверенности(certainty line), мы будем переходить к лотереям все более предпочтительным в смысле стохастического доминирования второго рода, ибо при фиксированном математическом ожидании выигрыша дисперсия будет непрерывно уменьшаться, достигая в точке пересечения с линией уверенности нулевого уровня (и вновь возрастая по мере дальнейшего удаления от исходной точки). Координаты точки А по обеим осям будут равны между собой и равны величине математического ожидания выигрыша: EW = Величина справедливой премии r* = W0 - EWтем самым будет соответствовать расстоянию(по оси абсцисс) между точкой А и исходной точкой, а рисковой премии r = EW- с будет отведен промежуточный интервал между достоверным эквивалентом и справедливой премией. • В завершение несколько слов о возможных экономических интерпретациях введенных понятий. Поскольку индивид безразличен между гарантированным получением c и участием в игре , т.е. и в том и в другом случае получает получает одинаковый уровень полезности, то рисковая премия r в справедливых играхможет интерпретироваться как эквивалентная вариация дохода (EV) по Хиксу Eu = u (c) = u(E(W) - r ) Соответственно, в неблагоприятных играх возможна подобная же экономическая интерпретация величины ( r*+ r) : Eu = u (c) = u [W0 - ( r + r*)] Рисковое вознаграждение или рисковая нагрузка(risk loading) и вероятностная премия. До сих пор рассматривались ситуации, в которых индивид вынужден был подвергнуться тому или иному риску, однако подобная постановка не вполне уместна, когда речь идет о возможных инвестициях в рискованные проекты со стороны агентов, изначально располагающих некоторой суммой и обладающих возможностью поместить эти средства в безрисковые активы. Предположим, индивид располагает некоторой суммой. Эта сумма может быть помещена им в безрисковые активы, что приведет к ее возрастанию до W0 . Если не склонному к риску индивиду предложат рискованное вложение первоначальной суммы на условиях, обеспечивающих то же самое (т.е. W0 ) математическое ожидание выигрыша, он безусловно откажется. Побудить его к рискованным вложениям могут только заведомо благоприятные условия предлагаемой игры, т.е. превышение математического жидания выигрыша в предлагаемой игре над уровнем W0. Естественной является постановка вопроса о минимально допустимой мере этой благоприятности, т.е. о том, насколько математическое ожидания выигрыша должно превысить W0 , с тем, чтобы индивид стал безразличен между участием и неучастием в игре. u(W0) = Еu(L). Графически проиллюстрировать величину этого превышения возможно, изобразив на рисунке дополнительную горизонтальную линию, проведенную на уровне u(W0). 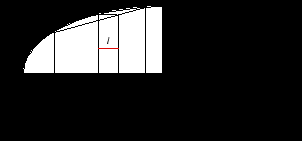 Рис.2.13 Собственно, следует предварительно оговорить возможность двоякого подхода к решению проблемы повышения математического ожидания выигрыша до уровня, соответствующего W* с двух различных точек зрения. Этого можно достичь улучшив выплаты при сохранении прежних вероятностей их получения и наоборот - увеличив вероятность получения лучшего приза(при сохранении прежнего уровня выигрышей). В первом случае, можно добиться безразличия не склонного к риску индивида между гарантированным обладанием W0 и рискованными инвестициями, имеющими такое же математическое ожидание выигрыша, предложив ему денежную компенсацию l = W* -W0за принятие этой справедливой игры. При этом вполне логичным представляется интерпретация подобной величины рискового вознаграждения или рисковой нагрузки( в англоязычной литературе называемой risk loading) как готовности индивида принимать компенсацию (WTA) или же компенсирующей вариации дохода, подобно тому как рисковая премия r т.е.плата, которую индивид готов заплатить за то, чтобы избежать уготованной ему справедливой игры,интерпретировалась нами как эквивалентная вариация дохода или готовность платить(WTР). Действительно, получение вознаграждения за риск позволяет индивиду, участвуя в игре, достичь того же уровня (ожидаемой) полезности, что и обладание суммойW0. В условиях, когда не существует обстоятельств , принуждающих индивида принять участие в справедливой игре, рисковое вознаграждение или рисковая нагрузка l будет более приемлемой денежной оценкой изменений в уровне (ожидаемой) полезности при принятии рискованной справедливой игры. Во втором случае, т.е. при фиксации уровня выигрышей, повышение математического ожидания выигрыша может быть достигнуто за счет приращения вероятности получения лучшего приза. Подобное приращение u(W0) = (р - получило название вероятностной премии  Рис.2.14. Итак, для не склонного к риску индивида, имеющего вогнутую функцию полезности, величина достоверного эквивалента лотереи будет ниже величины математического ожидания выигрыша, а вероятностная премия, рисковая премия и рисковое вознаграждение будут положительными: 1) с (F,u ) < E(W ) 2) Соответственно, для склонного к риску индивида, имеющего выпуклую функцию полезности выполняются обратные условия: 1) с (F,u ) > E(W ) 2)  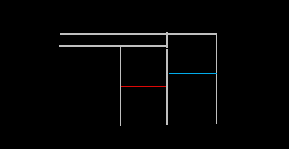
Измерение степени неприятия риска: меры абсолютной и относительной несклонности к риску Арроу-Пратта. Функция полезности Бернулли выпукла - для склонного к риску индивида, линейна - для индивида, нейтрального к риску , и вогнута - в случае, если он не склонен к риску. Логично предположить, что возрастание кривизны функции ведет к усилению степени склонности или же несклонности к риску.  Рис.2.16. Если функция полезности одного индивида является трансформацией функции полезности другого индивида, то второй индивид менее, более или в такой же степени склонен к риску (или несклонен к риску) в зависимости от того, является ли эта трансформация вогнутой, выпуклой или линейной. Более конкретно индивидуальные или иные ( порождаемые, к примеру, ростом первоначального богатства, т.е. W0 или же изменением размеров, получаемых денежных призов) различия в степени склонности либо несклонности к риску( в первую очередь, нас будет интересовать именно последнее) будут проявляться в различных оценках • рисковой премии r и вознаграждения за риск l, • вероятностной премии любой произвольно заданной справедливой лотереи L , например 1/2 о ( - Степень несклонности к риску будет тем выше, чем выше окажутся все эти характеристики.  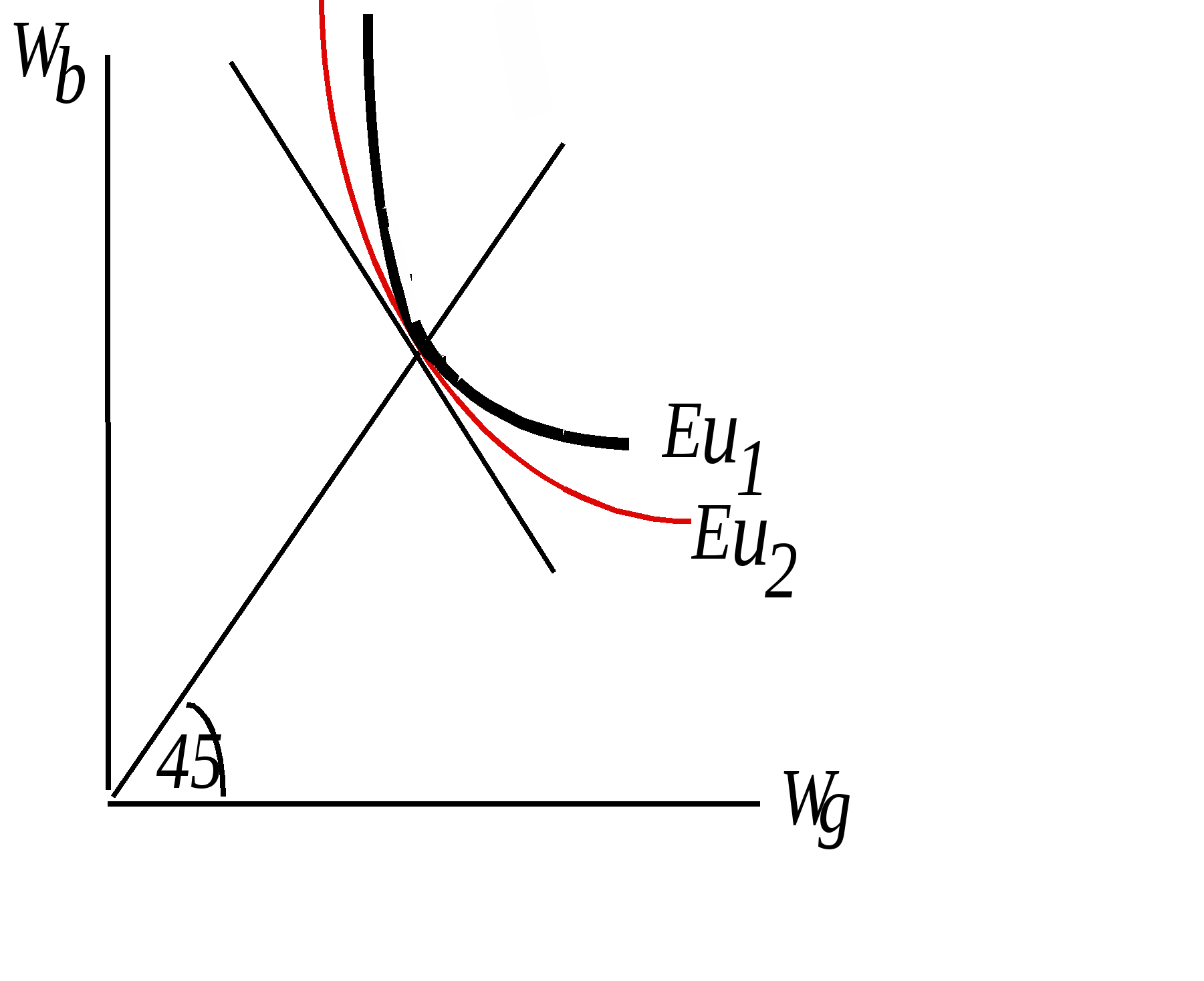
Зависимость будет обратной, если отправной точкой будет величина достоверного эквивалента лотереи с. Чем выше будет рисковая премия и, соответственно, чем ниже окажется достоверный эквивалент, тем менее индивид склонен к риску( или же - тем более он к нему несклонен). Разумеется, эта же зависимость будет справедлива и для несправедливых игр(корректировка на величину справедливой премии не меняет её характера). Иллюстрация различной степени несклонности к риску на пространстве условных благ традиционно сопровождается рисунком подобным рис.2.18.б. , свидетельствующим о том, что вторая производная функции Wb(Wg ,u1), т.е. 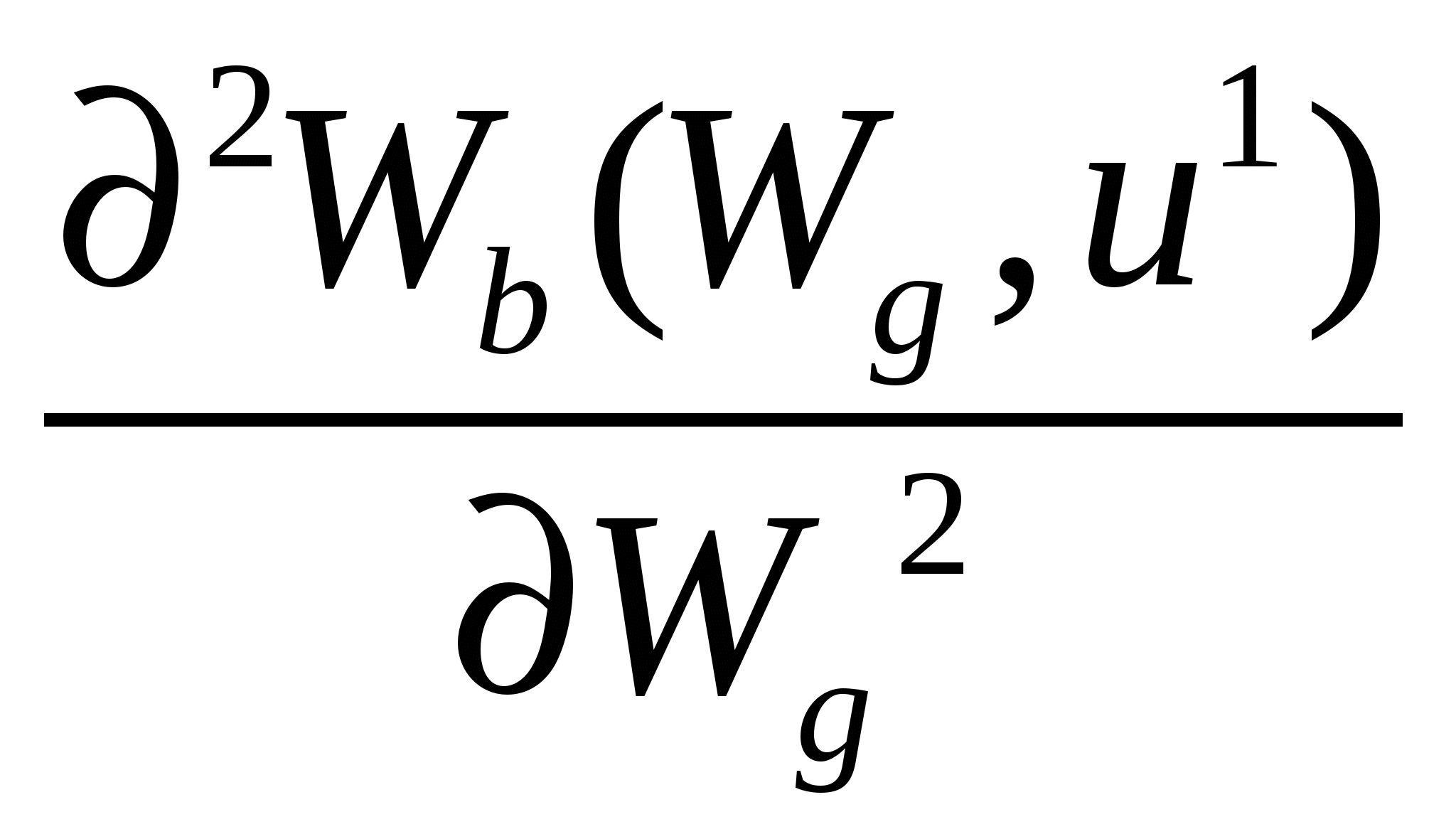 , превышает значение второй производной функции Wb(Wg ,u2) , превышает значение второй производной функции Wb(Wg ,u2) 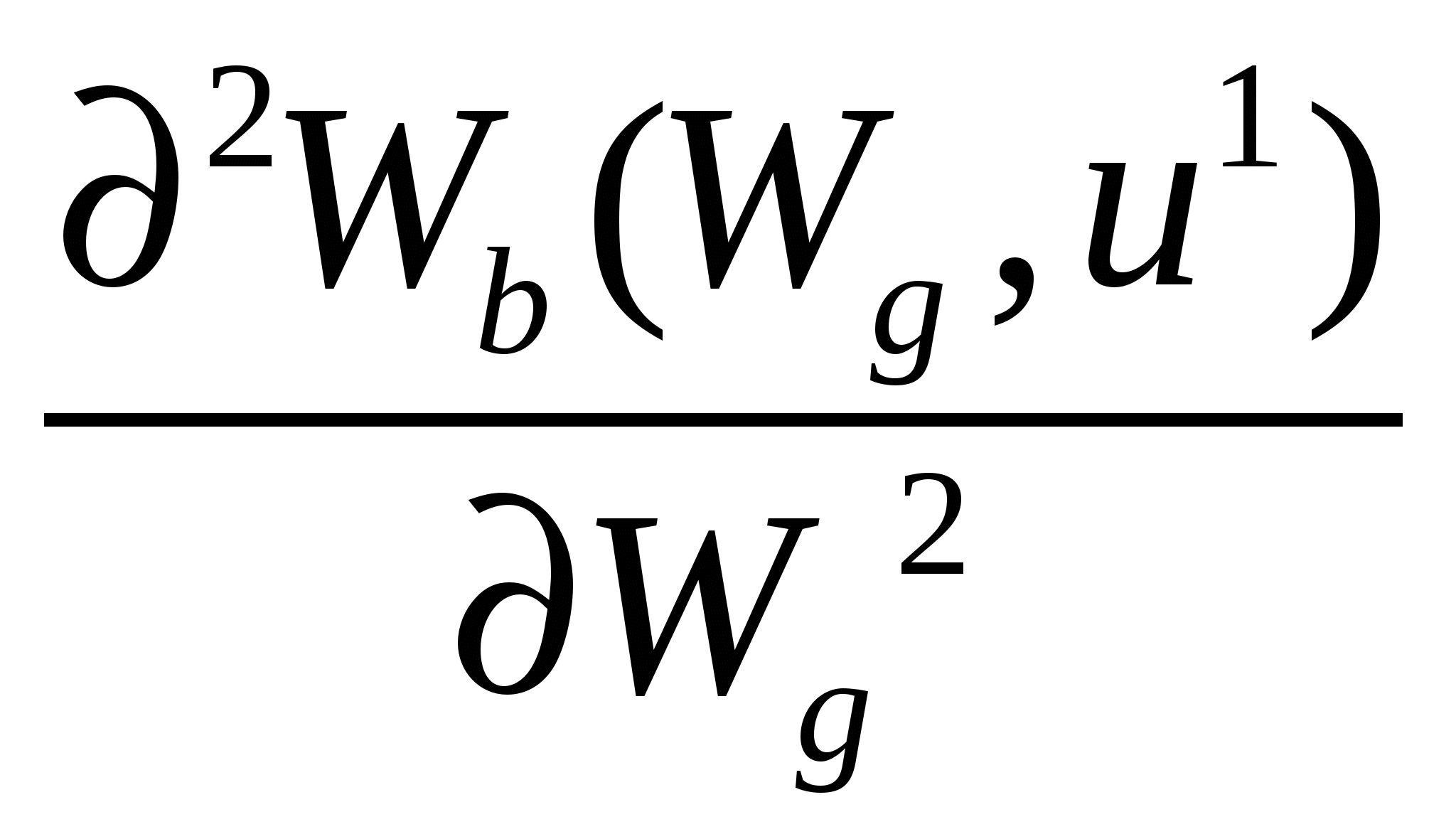 > > 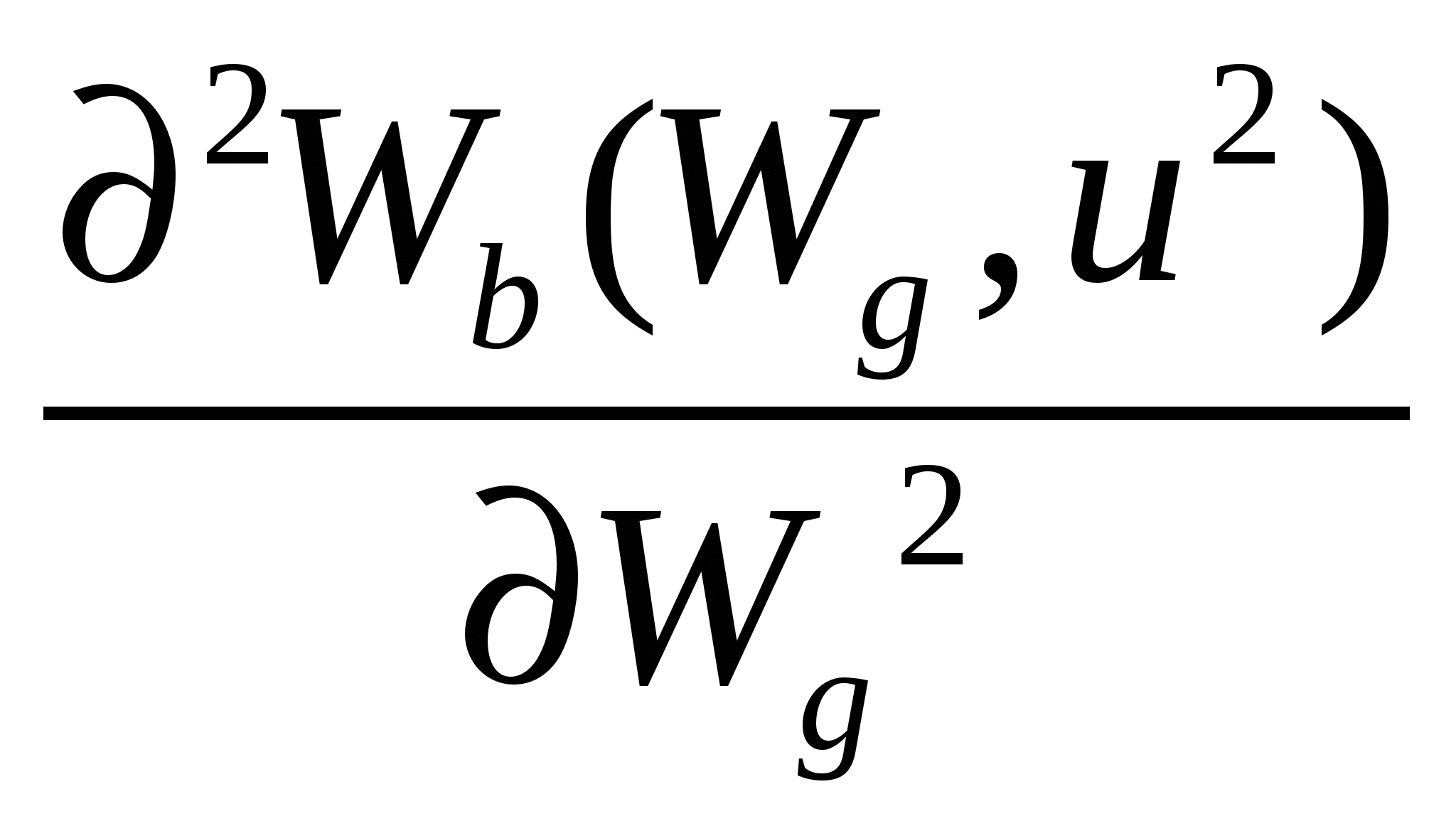 Необязательно! Этот результат можно вывести строго, продифференцировав предельную норму замещения MRS =- d Wb(Wg,u1) / dWg = 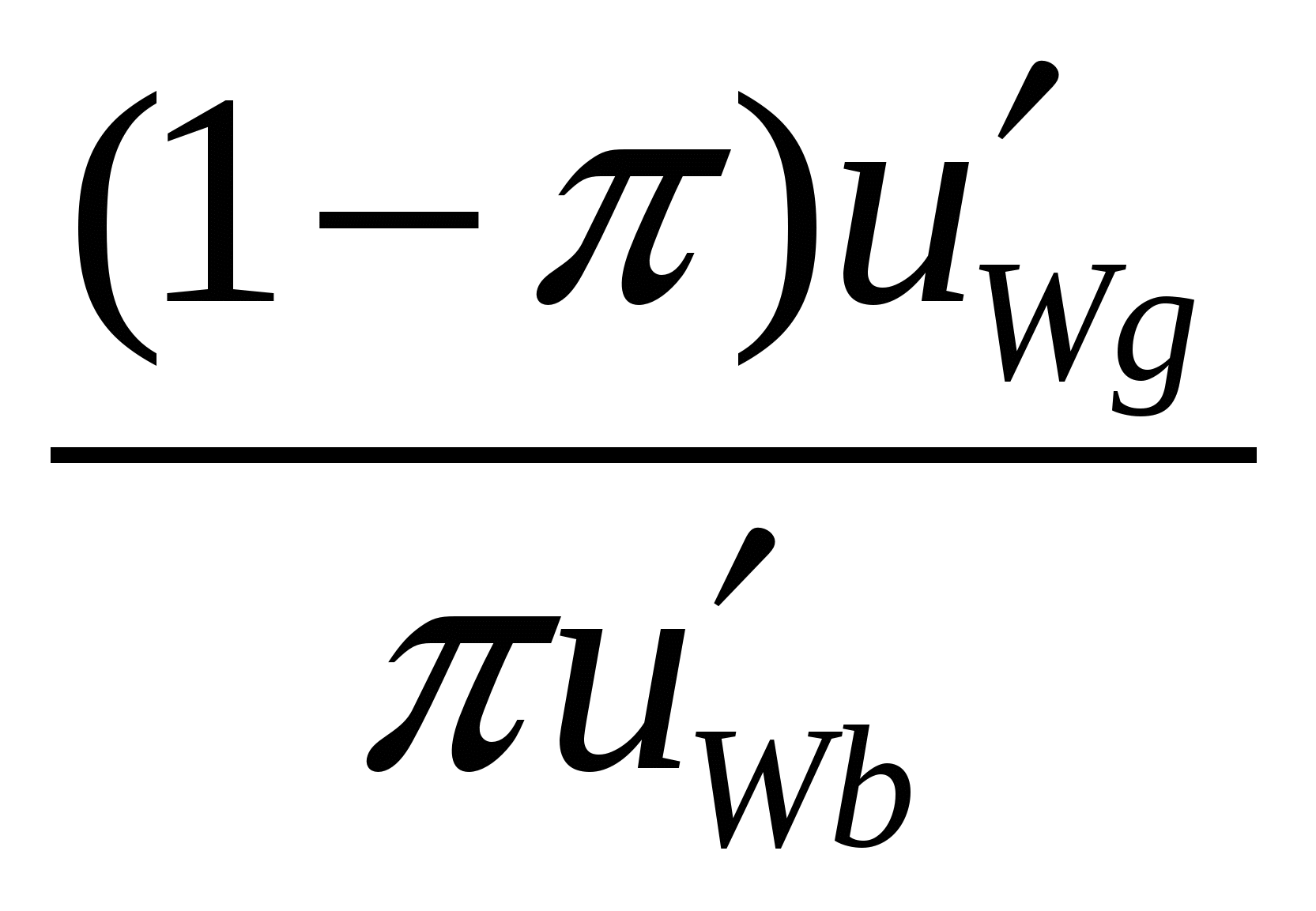 поWg поWg 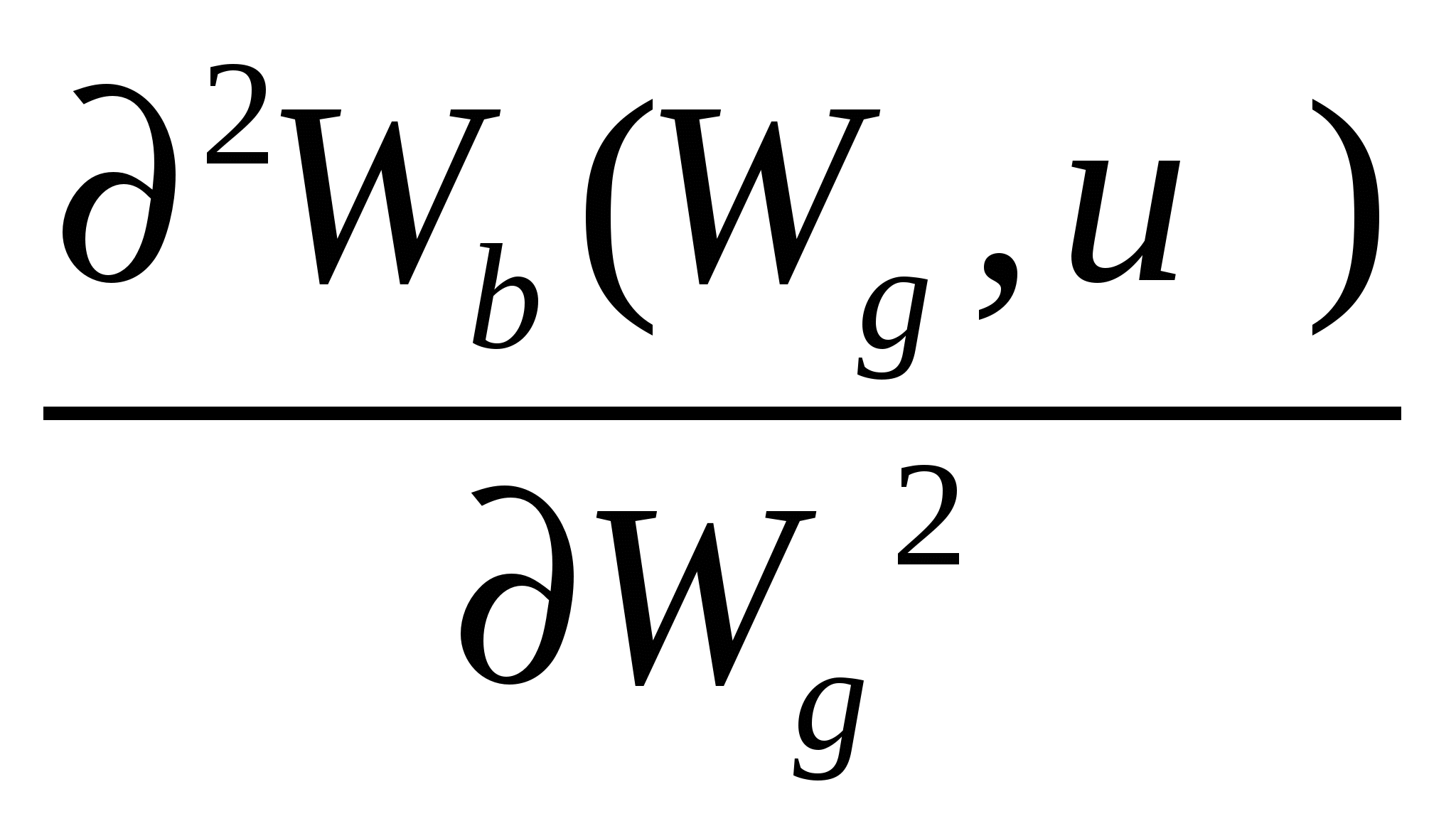 = =Поскольку на линии уверенности u'(Wg)= u'(Wb); u''(Wg)= u ''(Wb); Wb' = (1- [(1- Итак, предельная норма замещения в непосредственной близости от кривой уверенности убывает темпом пропорциональным [ u''(W) /u'(W)] , и чем выше степень кривизны кривой полезности Бернулли, тем выше степень кривизны кривых безразличия функции ожидаемой полезности. Мера абсолютной несклонности к риску Арроу-Пратта. Вторая производная функции полезности, характеризующая степень кривизны графика функции полезности Бернулли, представляется естественным кандидатом на роль индикатора степени несклонности к риску. Однако несмотря на то, что вторая производная(точнее ее знак)обеспечивает нас весьма полезной информацией о склонности, либо несклонности индивида к риску, ее нельзя использовать в качестве количественной меры, позволяющей сравнивать различных индивидов с точки зрения их отношения к риску(в частности, степени несклонности к риску). Причина этого коренится в единственности этой кардиналистской функции с точностью до аффинного преобразования, и вытекающей из этого обстоятельства произвольности значения второй производной. Впрочем, эта проблема может быть обойдена за счет введения нормирующего множителя. Весьма естественным решением является использование в качестве подобного нормирующего множителя величины, обратной первой производной. Такого рода показатель получил название меры абсолютной несклонности к риску Арроу-Пратта( Arrow-Pratt index of absolute risk aversion). Эта наиболее часто используемая мера несклонности к риску, названная по именам экономистов, независимо друг от друга разработавших ее в 1960-х годах, представляет собой дробь в числителе которой стоит вторая, а в знаменателе - первая производная функции полезности, взятую с обратным знаком. Знак "минус" добавляется с тем, что этот показатель несклонности индивида к риску был тем больше, чем менее индивид к нему склонен, т.е. был возрастающим по степени несклонности к риску. RA(W) = - u "(W)/ u '(W) = - d ln u '(W)/ dW абсолютная мера несклонности к риску Арроу-Пратта (функция полезности всегда возрастающая по Wu '(W)> 0) risk-averse u "(W)< 0 risk-lover u "(W) > 0 risk-neutral u "(W) = 0 Выбор именно отношения - u "(W)/ u '(W) в качестве меры абсолютной несклонности к риску был обусловлен, в первую очередь, тем обстоятельством, что для игр с незначительными выигрышами оно пропорционально тому количеству денег, которое в справедливой игре несклонный к риску индивид готов максимально заплатить за страховку , т.е. величине рисковой премии. Необязательно! Предположим несклонному к риску индивиду, обладающему денежной суммой W0 навязывается справедливая ( EW=W0 ) игра, выигрыши в которой при выпадении i -го состояния равны zi ( u (EW- r) = u (c) = Полагая величины zi незначительными, выпишем разложение в ряд Тейлора u(wi) = u(EW + zi )= u(EW)+ u '(EW) zi + 1/2u ''(EW) zi2 = u(EW) =u(EW)+1/2 u ''(EW) Оговорив, то, что рисковая премия является величиной того же порядка, что и выигрыши zi , мы можем получить и иное разложение для той же самой величины: Приравняем их друг другу: u(EW) - u '(EW) r ≈ u(EW)+1/2 u ''(EW) r ≈ (1/2) [ - u ''(EW)/ u '(EW)] где RA(W) =[ - u ''(EW)/ u '(EW)] - мера абсолютной несклонности к риску Арроу-Пратта. Итак, при несклонности индивида к риску абсолютная мера Арроу-Пратта пропорциональна рисковой премии, т.е. тому количеству денег, которое индивид готов максимально отдать за возможность не участвовать в справедливой игре. Соответственно, индивид 1 будет более несклонным к риску, чем индивид 2 тогда и только тогда, когда для любого распределения выигрышей F сумма, которую максимально готов заплатить за страховку индивид 1 - больше. RA1(W) ≥ RA2(W)r1F ≥ r2Fдля любого распределения выигрышей F. Поскольку размеры платы за страховку в реальной жизни наблюдаемы , то это дает информацию и о степени склонности к риску отдельных лиц и позволяет сравнивать между собой эти коэффициенты у отдельных групп людей, оценивая, таким образом, их склонность к риску. При рассмотрении поведения индивида, не склонного к риску, принципиально важным является вопрос о том, возрастает или убывает абсолютная мера Арроу-Пратта по мере роста богатства. Можно предположить, что с ростом богатства готовность платить за страховку сокращается, т.к. снижающаяся предельная полезность денег делает возможные потери менее ощутимыми. Но это может быть неверным, т.к. и возможный выигрыш также становится менее ощутимым. Таким образом, конечный результат малопредсказуем и там, где это возможно, целесообразно абстрагироваться от воздействия уровня богатства на степень несклонности индивида к риску, полагая ее неизменной. В этой связи уместно обратиться к рассмотрениючасто используемых в экономическом анализе так называемых функций полезности CARA (Constant Absolute Risk Аversion utility functions) , для которых изменение уровня богатства не оказывает влияние на готовность индивида платить за страхование, т.е. размер рисковой премиине зависит от величиныW. Функции полезности с постоянной абсолютной степенью несклонности к риску(CARA). RA = - u ''(W)/ u '(W) = const Для того, чтобы вывести вид функций полезности, характеризуемых этим свойством, решим соответствующее дифференциальное уравнение или же просто проинтегрируем это уравнение дважды. Результат первого интегрирования: l n u '(W)= C1 - RAW Результат второго интегрирования: u (W) = C2 - RA-1 еxp ( k1 - RA W) Обозначим а = C2 ; b = RA-1еxp C1 . Итак, функции полезности u (W)= а - b еxp ( - RA W) описывают предпочтения индивида с постоянной абсолютной несклонностью к риску. Cобственно, поскольку эта кардиналистская функция полезности единственна с точностью до аффинного преобразования, константы могут быть опущены, и тогда u (W)= - еxp ( - RAW) . Мера относительной несклонности к риску Арроу-Пратта. Собственно, вопрос о степени несклонности индивида к риску может анализироваться и под несколько иным углом зрения. А именно - не с позиций различий в величине денежной суммы, которую индивид готов истратить на покупку страховки , а с точки зрения того, как меняется доля средств, которую индивид максимально готов выделить на оплату страховки. В подобном случае уместно говорить, не об абсолютной, а о относительной несклонности индивида к риску. Мера относительной несклонности к риску рассчитывается на основе абсолютной мерой несклонности к риску в соответствии со следующей формулой: RR(W)= W RA(W) 1) Функции полезности с постоянной относительной несклонностью к риску (сonstant relative risk aversion - CRRA) Как правило, люди менее склонны к риску , чем это предполагается логарифмической функцией полезности u(W) = ln (W) , для которой RA(W) = хотя во многих случаях она обеспечивает приемлемое приближение. В свете этого правдоподобным является предположение, что RR(W) = W RA(W) ≈ const (во всяком случае для небольших изменений вW) Для того, чтобы получить общий вид функций CRRА, воспользуемся ранее опробованным приемом, т.е. выпишем коэффициент относительной несклонности к риску, и полагая его равным некоторой константе, проинтегрируем дважды, после чего, учтя единственность функции с точностью до афинного преобразования, получим u (W)= - W - RR+1 Функции САRA и CRRA в совокупности образуют класс HАRA(hyperbolic absolute risk aversion) функций или LRT (linear risk tolerance)функций, примечательных тем, что для индивидов, чьи вероятностные ожидания совпадают, а функции полезности принадлежат к одному(точнее - одному и тому же) из подклассов этого класса функции(их всего три - экспоненциальные(САRA) , степенные(СRRA) и логарифмические функции(СRRA)), парето - оптимальные контракты будут линейными(подробнее об этом будет сказано ниже). u (W) = - еxp ( - RAW) u (W) = - W- RR+1 u (W) = ln W |
