1 Неопред БИ 12. 1. Неопределенность информации
 Скачать 1.17 Mb.
|
Распределение и диверсификация рисков.Объединение рисков. Индивидуальные и системные риски. а) риски L индивидуальные и негативно коррелированные Воспользуемся диаграммой Эджворта для анализа взаимодействия, возникающего между индивидами, столкнувшимися с независимыми негативно коррелированными рисками. Негативная коррелированность рисков означает, что в состоянии 2 потери терпит индивид 1, в то время как в состоянии 1 - индивид 2.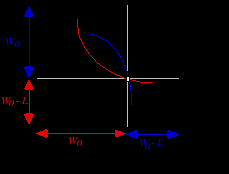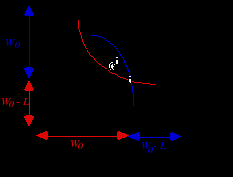  
Заметим, что обмен между индивидами взаимными обязательствами на случай наступления того или иного состояния(state--contigent claims to wealth) имеет смысл только до того момента, когда станет ясно, какое из двух возможных состояний реализовалось. Простоты ради будем полагать, что оба индивида первоначально располагают одинаковой суммой денег W0 , и подвергаются одинаковому риску понести потери L . Подобные условия обусловливают равенство сторон диаграммы Эджворта (длина стороны квадрата равна 2 W0 - L). То, что диаграмма Эджворта имеет квадратный вид, предполагает отсутствие общественных или системных рисков (уровень суммарного богатства в различных состояниях не варьируется). Если же говорить о рисках индивидуальных, то стремясь застраховать себя от них, индивиды могут заключить договор, в соответствии с которым "счастливчик" всякий раз делится с "неудачником" некоторой частью своего богатства. При независимости функций полезности Бернулли от выпавшего состояния мира и совпадении оценок вероятности выпадения различных состояний, контрактная кривая будет представлять собой диагональ квадрата, совпадая с линиями уверенности агентов. Действительно, на линии уверенности w1 = w2, а, соответственно,  что обеспечивает совпадение предельных норм замещения с отношением вероятностей, а, следовательно, и друг с другом :  Это делает не просто возможным, но и оптимальным - предоставление всем индивидам полной страховки. Строго говоря, размеры платежей могут быть различными - все зависит от того, насколько сильны позиции каждой из сторон в ходе торга(т.е. то, что по английски называется a bargaining power - Рис.3.1.б). В частности, при равном влиянии участников возможно заключение "справедливого" контракта, предполагающего изъятие у каждого из них денежной суммы, равной справедливой премии (сдвиг влево вверх вдоль линии постоянного ожидаемого выигрыша вплоть до точки на кривой уверенности). Подобное распределение предполагает, что первый индивид в любом из выпавших состояний получает сумму, равную математическому ожиданию выигрыша, т.е. W0-  L, где - вероятность выпадения второго, неблагоприятного для него "состояния мира", а второй - W0- (1-) L. Например, при = 1/3 первый индивид в благоприятном для него первом состоянии заплатит второму индивиду L/3, но во втором состоянии получит компенсацию, равную (2 L/3). В результате он будет полностью застрахован, получая в любом из возможных состояний сумму, равную математическому ожиданию его выигрыша, т.е. W0- (L/3). Полная страховка будет обеспечена и второму индивиду, но уровень его богатства в обоих состояниях будет ниже(ввиду более высокой вероятности того, что именно он понесет потери) и равенW0- (2 L/3).Как бы то ни было, объединение риска в условиях, когда его осуществляют два не склонных к риску индивида с идентичными, но негативно коррелированными распределениями выигрышей, позволяет им обоим повысить уровень получаемой полезности. б) риски индивидуальные - равные, но некоррелированные (независимые). Описанное выше объединение рисков имеет смысл и в случае независимых распределений выигрышей индивидов. Как и прежде, полагая равенство сумм W0, которыми первоначально располагают индивиды, и совпадение размеров возможных потерь L, предположим, что оба индивида сталкиваются с одинаковой вероятностью понести эти потери и для каждого из них она равна .В результате возможно выпадение одного из четырех состояний:
Ожидаемая полезность каждого индивида взятого в отдельности, т.е. Еu(1) = u(W0 - L) + (1-)u(W0)может быть увеличена, в частности, если индивиды объединят свои риски, договорившись делить пополам суммарное богатство, выпадающее в каждом из состояний. В подобном случае ожидаемая полезность каждого индивида превысит первоначальный уровень(в предположении, что индивиды несклонны к риску, т.е. функция u(W) вогнута) : Еu(2) =(1 - )2u(W0 )+ 2u(W0 - L) + 2(1-)u((2W0 - L)/2) , Еu(2) - Еu(1) = (1-)u(W0) (1-)u(W0 - L) + 2(1-)u((2W0 - L)/2) = (1-) {[u((2W0 - L)/2) - u(W0 - L)] - [u(W0 ) - u((2W0 - L)/2)]} > 0
|