1 Неопред БИ 12. 1. Неопределенность информации

• Название: 1. Неопределенность информации
• Дата: 19.09.2018
• Размер: 1.17 Mb.
• Имя файла: 1 Неопред БИ 12.doc
• Тип: Документы; #51096
• страница: 4 из 6

Выбор в условиях неопределенности.

Полезность индивида обусловлена не только его финансовым положением, но и тем, в каком "состоянии мира", получается тот или иной выигрыш.

До сих пор, рассматривая поведение потребителя в условиях неопределенности, мы несколько отошли от подхода, который использовался ранее в теории потребительского выбора- максимизации полезности в рамках заданного бюджетного ограничения. Теперь нам предстоит вернуться к прежним моделям. Но прежде, чем сделать это следует ввести новое понятие.

Условное благо (contingent commodity)- благо, которое потребитель получает только при определенном состоянии внешнего мира. Это не просто 1 доллар, значащий в „плохие времена” совсем не то, что в хорошие. Это 1 доллар, получаемый , к примеру , только в случае, если настали „плохие времена” Пример: получение страховки в случае угона автомобиля. Тогда, когда индивид оплачивает стоимость страховки, он тем самым оплачивает получение денег в плохие времена, т.е. приобретает условный товар.

Покупка двух товаров „1 доллар в плохие времена” и „1 доллар в хорошие”: индивид оплачивает их заранее, но доставлен будет только один товар, т.к. времена будут или плохими или хорошими. Ставки делаются на всех лошадей одновременно, но выиграет только одна.

Рынки на условные товары могут быть раздельными, и в принципе может быть куплен только один из условных товаров.

Итак, предположим, что первоначально потребитель располагал суммой W₀.

С вероятностью  он может понести потери (losses) L. С тем, чтобы обезопасить себя от них он может приобрести страховку, согласно которой в случае возникновения этих потерь ему будет выплачено страховое покрытие сумма q в том случае, если в качестве платы за страховку будет внесена сумма pq, где p<1

W_b = W₀ - pq - L + q

W_g = W₀ - pq

Рис.2.19.

На рисунке видно, гарантированное получение математического ожидания выигрыша u(EW^R ) превысит ожидаемую полезность игры:

u(EW^R ) > Eu ^R .

Итак, на какую сумму застрахуется потребитель, стремящийся к максимизации ожидаемой полезности ?

max_q U(L) = u (W₀ - L - pq + q) + (1 -) u( W₀ - pq )

Выпишем условие первого порядка, для чего приравняем нулю производную ожидаемой полезности индивида по q

F.O.C. u '(W₀ - L+ q*(1-p))(1- p) + (1-)u '(W₀ - pq*)(- p) = 0

(1 -)u '(W₀ - pq*) / u '(W₀ - L+ q*(1-p)) =

Графически это может интерпретироваться совпадение (тангенсов) углов наклона

бюджетной линии

=

и кривой безразличия

MRS =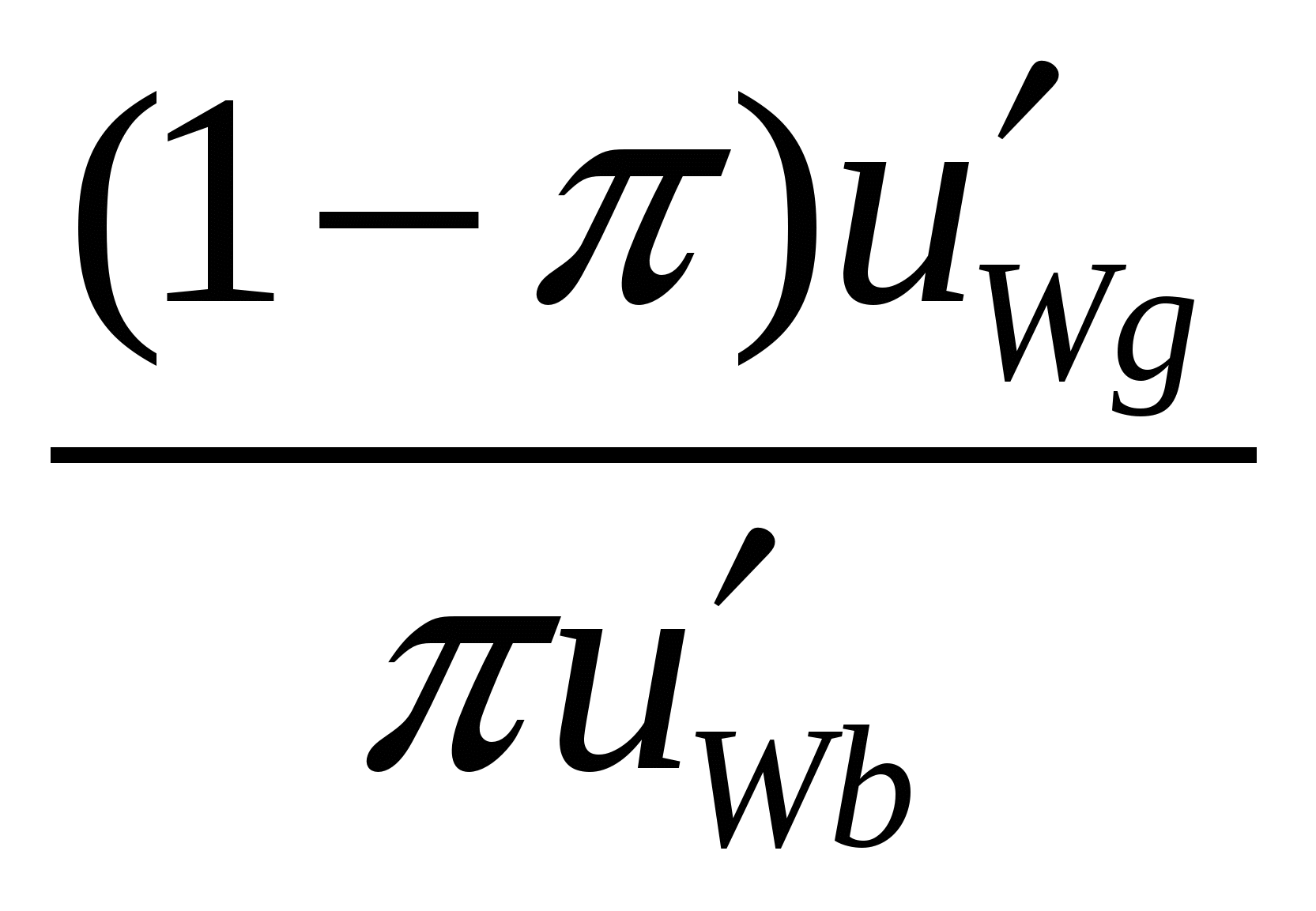

Наклон бюджетной линии .

Предположим, что индивид застраховался, внеся платеж pq, дающий ему ( в случае наступления страхового случая) право на получение q .

Рис.2.20.

Рассмотрим подробно прямоугольный треугольник, гипотенузой которого является бюджетная линия и определим тангенс угла ее наклона

Рg / Р_b= АC/ СB = [(W₀- L - pq + q ) - (W₀- L)]/ [W₀ - (W₀- p q)]=

= (q - pq)/ p q =

p - цена одного доллара в плохие(bad) времена или Р_b

(1 - p) - цена одного доллара в хорошие(good) времена или Рg

Тангенс угла наклона бюджетной линии Рg /Р_bпоказывает, в каком соотношении потребитель может на рынке страховых услуг поменять доллар в хорошие времена на доллар в плохие.

Если, к примеру, Р_b = p = 0.2, а Рg = (1 - p) = 0.8 то, сокращение потребления на 1 доллар "в хорошие времена" позволяет увеличить потребление на 4 доллара - "в плохие".

Уровень платы за страховку p, устанавливаемый страховой компанией.

Если страховой случай не произойдет, то прибыль страховой компании составит pq,

если он все же наступит, то с учетом предстоящей выплаты страховки прибыль страховщика сократится до (pq - q) . Определимматематическое ожидание прибыли страховой компании : (1-)pq + (pq - q)

а) Если рынок страхования конкурентен то, долгосрочная ожидаемая прибыль страховой фирмы должна быть равна нулю:

(1-)pq + ( pq - q) = 0

что, как несложно убедиться, раскрыв скобки, предполагает совпадение уровня платы за страховку с вероятностью наступления страхового случая: p =.

Таким образом, введение в модель предположения о справедливости страхового рынка имеет своим следствием установление в нейплаты за страховку, равной вероятности наступления страхового случая .В подобном случае, т.е. при p = , линия постоянного математического ожидания выигрыша, наклон которой равен (1-)/ совпадает с бюджетной линией, наклон которой - (1-p)/р.

Условие первого порядкаможет быть приведено к следующему виду

= 1

и, соответственно, , откуда следует, что

W_b = Wg W₀ - L+ q^*(1-p)= W₀ - p q^* q^*= L

Вывод: не склоненный к риску потребитель, для которого MRS будет убывать, на справедливом рынке страхования будет стремиться застраховать полную величину своих возможных потерь: q^*= L , причем в качестве платы за страховку он будет вносить денежную сумму, равную по своей величине лишь справедливой премии.

Из последнего с очевидностью следует, что уровень ожидаемой полезности застрахованного индивида будет выше,чем индивида незастрахованного.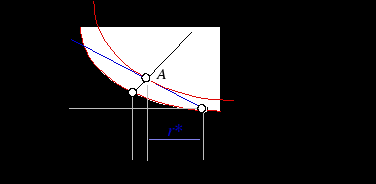



Рис.2.21.

Максимально индивид готов заплатить за страховку r^*+ r, но на справедливом рынке страхования он может обеспечить полное покрытие потерь, внеся в виде платы за страховой полис всего лишь денежную сумму, равную справедливой премии r^*.
б). Ситуация кардинально меняется в том случае, если рынок страхования полагается неконкурентным(несправедливым) и стоимость страхования превышает вероятность наступления страхового случая, т.е. p >. В подобном случае

< 1,

и, следовательно, оптимум достигается в точке, где

Wg > Wb W₀ - pq^*> W₀ - pq^*- L + q^* q^*< L (см. рис.2.22.а)

При несправедливом( неблагоприятном) страховом рынке индивид, стремящийся полностью застраховать свои потери, будет вынужден внести сумму, превышающую справедливую премию( fair premium )

r^*= W₀- E(W).

Cоответственно, отнюдь не очевидным становится выбор им варианта полного страхования, ранее основывающийся на том, что не склонный к риску индивид, должен был заведомо предпочесть справедливой игре гарантированное получение математического ожидания выигрыша. Поскольку в данном случае индивид, стремясь застраховаться полностью, будет в итоге гарантированно располагать суммой, меньшей E(W), он страхует лишь часть своих возможных потерь, заключая договор частичного страхования, т.е. берет часть риска на себя. Рис. 2.22.б иллюстрирует предпочтительность такого решения по сравнению с выбором варианта страхования, предполагающего полное покрытие возможных потерь.

Рис.2.22.а

Рис.2.22.б

Кстати говоря, неравенство платы за страховку вероятности наступления страхового случая может быть порождено не только неконкурентным характером рынка страхования, но и вполне естественными( в том числе и на конкурентном рынке) различиями в оценке вероятности наступления страхового случая у двух сторон, заключающих договор. Даже полагая рынок конкурентным, мы в этом случае не сталкнемся с контрактами полного страхования. Страховая компания в этом случае назначает плату за страховку p , руководствуясь своей оценкой вероятности наступления страхового случая, в то время как агент, покупающий страховку выбирает тот или иной объем погашения q^* , основываясь на собственных представлениях о уровне 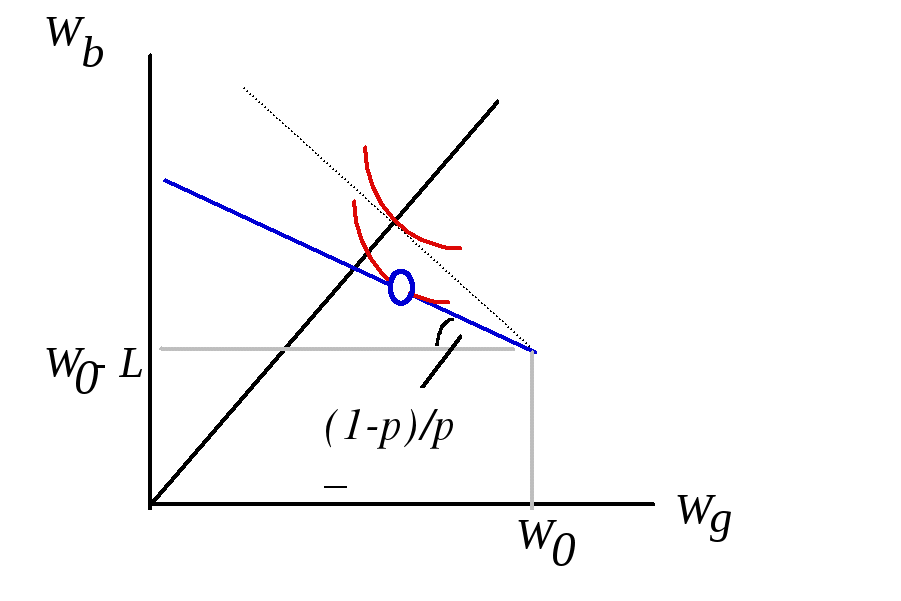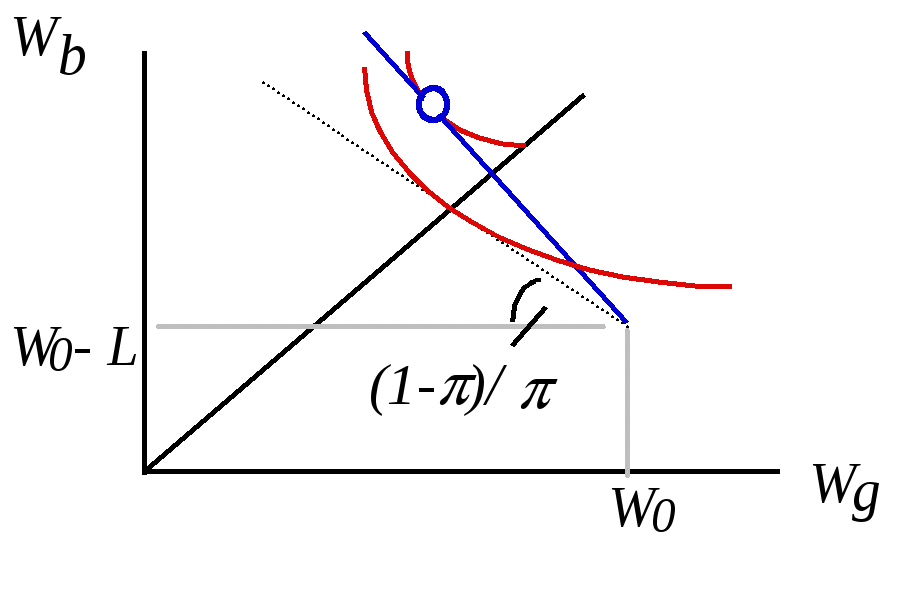 . Причем в зависимости от того, как соотносятся эти оценки вероятности наступления страхового случая, речь пойдет либо о неполном, либо о избыточном страховании.

Рис.2.23.а Hеполное страхованиe: p >

Рис.2.23.б  Избыточное страхование:  p <

Собственно, это замечание есть лишь небольшой фрагмент весьма обширной темы, посвященной обсуждению объективных и субъективных вероятностей. Следуя Найту, часто проводят грань между ситуациями риска и неопределенности именно по этой линии, разделяющей вероятности объективные(падение монеты той или иной стороной) и субъективные( возможность резкого падения курса рубля по отношению к доллару). Впрочем, не лишена резона мысль о том, что даже в простейшем случае, когда речь идет о бросании монеты, индивид может присваивать выпадению той или иной ее стороны вероятности не равные 1/2 , если он допускает возможность обмана, не говоря уже о статистических данных, которые могут интерпретироваться весьма и весьма различным образом. Например, если даже точно известна средняя вероятность рождения ребенка того или иного пола, индивид может весьма существенно корректировать ее применительно к конкретной ситуации. Иначе говоря, как правило мы имеем дело с вероятностями субъективными, а, соответственно, типичными являются несовпадения оценок вероятности того или иного события, даваемые разными агентами.

Сравнительная статика.

Каким образом скажется на выборе потребителя(его спросе на страхование) изменения

А. в вероятности наступления страхового случая;

В. в степени несклонности индивида к риску ;

С. в уровне первоначального богатства ;

D. в уровне платы за страховку.

A. Последствия изменения вероятности наступления страхового случая.

Как повлияет на вид кривых безразличия и выбор индивида повышение вероятности наступления страхового случая ?

Несложно догадаться, что при повышении вероятности наступления страхового случая наклон кривых безразличия станет более пологим (< 0 ).

(Формально : возьмем частную производную предельной нормы замещения MRS = 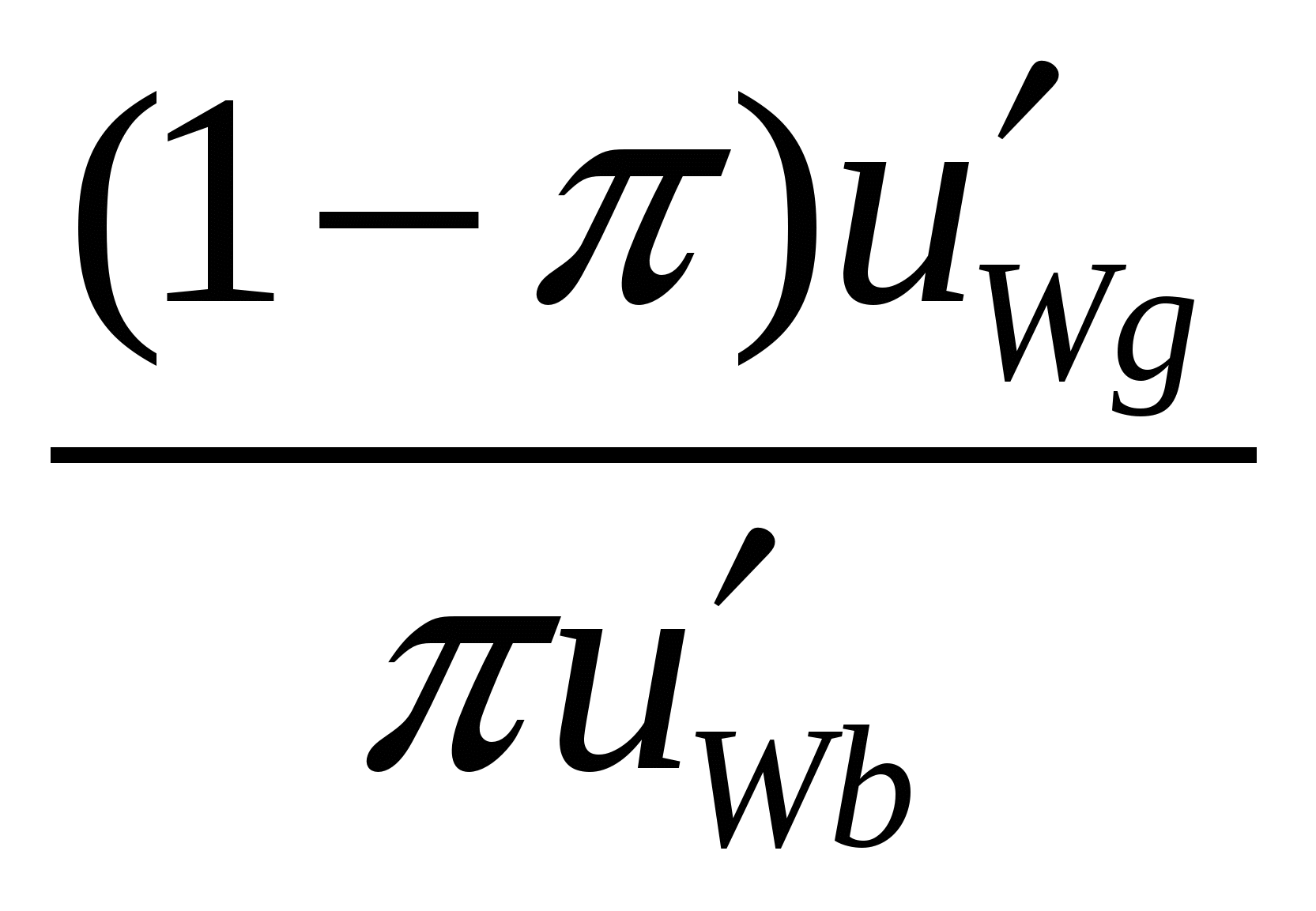по : = (-) < 0 ) . Это (при сохранении платы за страховку) должно привести у увеличению спроса на страхование.
Рис.2.24
Этим утверждением мы и ограничимся, но следует иметь в виду, что изучение контрактов, заключаемых на рынке страхования в условиях информационной асимметрии (т.е. отсутствия у страховой компании информации о вероятности наступления страхового случая у данного индивида) сопровождается сходными рисунками, в которых различная вероятность наступления страхового случая (высокая - H или низкая - L ) приписывается агентам различного типа.
В. Изменение степени несклонности к риску.

Повышение степени несклонности индивида к риску, как уже отмечалось усилит степень кривизны кривых безразличия, а , соответственно, и величину спроса на

страхование.

Рис.2.25.а

Рис.2.25.б

Собственно, определение абсолютной степени несклонности к риску построено как раз на основании оценки готовности индивидов платить за страховку . Как уже отмечалось при несклонности индивида к риску и незначительности выигрышей в справедливой игре абсолютная мера Арроу-Пратта пропорциональна тому количеству денег, которое человек готов максимально заплатить за страховку: индивид 1 будет более несклонным к риску, чем индивид 2 тогда и только тогда, когда для любого распределения выигрышей F сумма, которую максимально готов заплатить за страховку индивид 1 - больше.

R_A¹(W) ≥ R_A²(W) r¹_F ≥r²_F для любого распределения выигрышей F.
С. Изменения в уровне первоначального богатства.

1) Добавление некоторой суммы( некой случайной величины, имеющей распределение F )к исходному богатству(при сохранении величины возможных потерь)приведет к изменению первоначально наделенности и сдвигу исходной точки к северо-востоку по линии, имеющей наклон 45 градусов. Воздействие этого сдвига на величину спроса индивида на страхование обусловлено тем, каким образом меняется вдоль этой кривой предельная норма замещения. Определить этодовольно просто, воспользовавшись ранее уже полученным выражением для 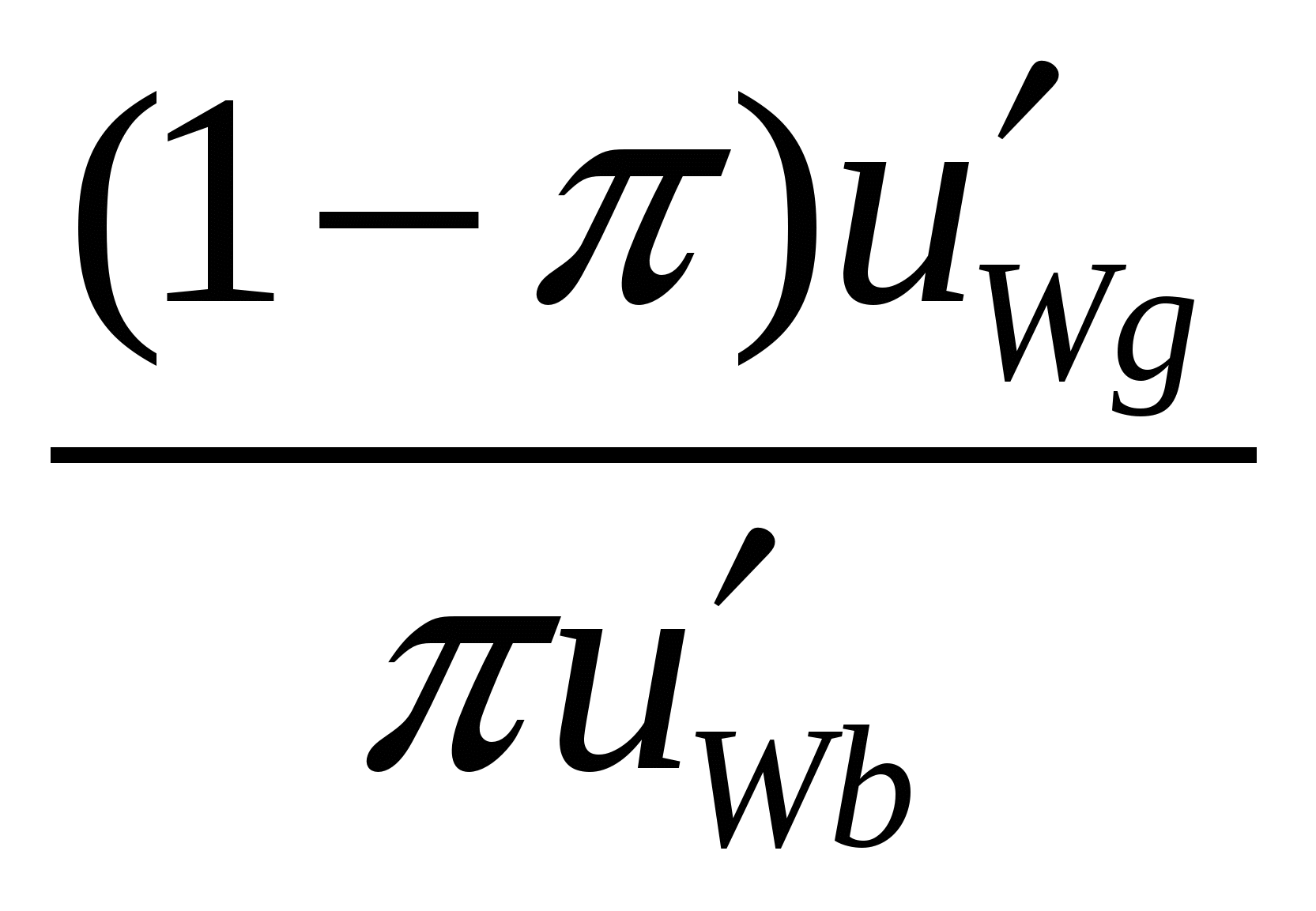MRS /W_g и учтя, что при движении вправо вверх под углом в 45 градусов = 1 . Итак

= (){( - }=

= { } = MRS[R_A(W_b) - R_A(Wg) ]

рис. 2.26

При постоянстве меры абсолютной несклонности к риску (САRA) MRS /W_g = 0,

и величина r не зависит от уровня первоначального богатства W₀, т.е. для индивида с постоянной степенью несклонности к риску страховая премия, которую он готов будет отдать за избавление от риска (например, возможной потери $ 50 ), будет независима от величины W₀: оказавшись в рискованной ситуации индивид будет страховаться одинаково , обладая как $ 100 , так и $ 100 000. Разумеется, при столь значительном варьировании уровня богатства, гипотеза о постоястве абсолютной несклонности к риску выглядит малоубедительной, но при относительно небольших колебаниях в уровне богатства, она может служить вполне правдоподобной упрощающей предпосылкой.

рис. 2.27.а Возрастающая абсолютная несклонность к риску: < 0

рис. 2.27.б Снижающаяся абсолютная несклонность к риску : > 0

Для заметных изменений в уровне первоначального богатства, впрочем, она будет недостаточно корректна. В подобном случае более реалистичной предпосылкой будет предположение о готовности индивида отдать в качестве платы за страховку тем меньшую сумму, чем больше уровень W₀ , т.е. снижение R_A с ростом богатства . Оно будет выполняться, в частности, при принятии гипотезы о том, что в качестве функции полезности может быть использована логарифмическая функция u(W)= ln (W), для которой R_A(W)= - (- W^-2)/ W^-1 =

2) Уровень богатства в "плохом" состоянии составляет некую долю от уровня богатства в "хорошем состоянии": W_b = kW_g = k =

Определим, каким образом меняется наклон кривых безразличия при движении вправо вверх по исходящему из начала координат лучу, тангенс угла наклона которого равен k . Итак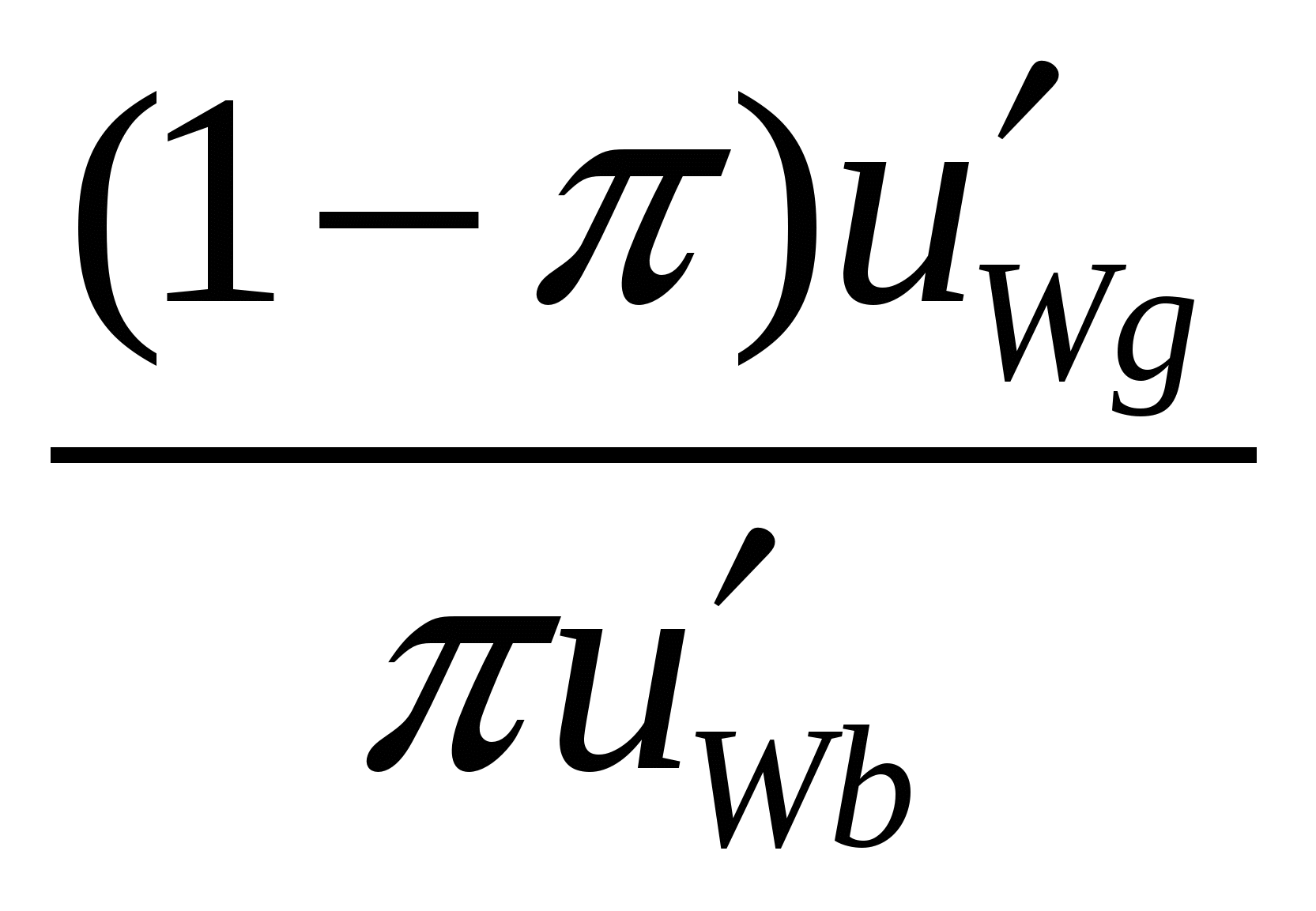

== {( - k } =

= ( - k) =

= MRS( - ) =

= ( W_g -  W_b )

= (R_R(W_b) - R_R(Wg) )


Итак, индивид, функция полезности которого характеризуется постоянством относительной меры несклонности к риску всегда будет готов пожертвовать одной и той же долей ожидаемого выигрыша(т.е. мультипликативной рисковой премией), сталкиваясь с риском в форме k W₀ , где W₀ является величиной фиксированной, а k - не зависящей от W₀ случайной величиной , с заданной вероятностью распределения F.

рис. 2.28.а Постоянная относительная несклонность к риску

рис. 2.28.б Убывающая относительная несклонность к риску

Если относительная несклонность индивида к риску возрастает, то по мере роста W₀возрастает и мультипликативная страховая премия, т.е. R_R(W) есть возрастающая функция от W. Принято полагать, что при значительных изменениях в уровне располагаемого богатства возрастающая относительная несклонность к риску представляет собой наиболее реалистичный случай, подтверждением чему, кстати говоря, может служить распространенность различного рода лотерей преимущественно в бедных странах(при незначительных - можно ограничиться гипотезой постоянства относительной несклонности к риску ) .

Кстати, ситуации, анализ которых упрощает введение относительной меры несклонности к риску, часто возникают в реальности. Например, доход на инвестиции(вклад) может зависеть от размера вклада, а при падении курса акций происходит потеря определенной доли богатства.

D. Изменение уровня платы за страховку.

Изменение платы за страховку, т.е. p , приведет к изменению в спросе на страхование, которое можно анализировать, как это традиционно и делается при анализе выбора потребителя, выделяя эффект замещения (АВ) и эффект дохода (ВС).

рис. 2.29.а Эффект дохода равен нулю.

рис. 2.29.б Эффект дохода положителен.

Различие состоит лишь в том, каким образом определяется эффект дохода. Он будет нулевым, в том случае, если кривая ВС будет параллельна линии уверенности, положителен - в случае убывающей абсолютной несклонности индивида к риску и отрицательным - при ее возрастании.

Необяз!

Декомпозиция общего приращения в величине спроса на страхование

q/p может быть получена cледующим образом (см. теорему о неявной функции)

q*/p = - V_qp ''/ V_qq''= - (² V/qp)/( ²V/q²)

где V/q = u '(W₀- L+ q*(1-p))(1- p) + (1-)u '(W₀ - pq*)(-p)= 0

(условия первого порядка в модели формирования спроса на страхование)

²V/qW = -u ''(W_b)(1- p)+ (1-)u ''(W_g)p]

²V/qp = [ -u '(W_b)+u ''(W_b) q*] - (1-)[ u '(W_g)) +(1-)u ''(W_g)) q*]=

-[u '(W_b)+(1-)[ u '(W_g)] - q*[ u ''(W_b)(1- p)+(1-)u ''(W_g)p) q*] =

- Eu '- q* V_qW ^''

q*/p = - V_qp ''/ V_qq''= (Eu '+ q* V_qW ^'')/V_qq''= Eu '/V_qq''+ q* V_qW ^''/V_qq''=

Eu '/V_qq''- q* (q*/W) (некий аналог уравнения Слуцкого)

SE IE

Кстати , пользуясь сходным методом можно непосредственно вывести выражения для производных q/ W_{0 ,} q/ Lи т.д.

Расширенная функция ожидаемой полезности.

Весьма важным направлением дальнейшего совершенствования анализа поведения индивида в услових неопределенности является попытка учесть зависимость вида функции полезности Бернулли от того, какое "состояние мира" будет реализовано . Действительно, удовлетворенность индивида уровнем своих доходов, как правило, обусловлена уровнем не абсолютного, а относительного богатства, состояние здоровья влияет на полезность денег и т.д. и т.п.. Тем самым единая функция полезности Бернулли u(W) уступает место некоему семейству функций u_s(W), s S, каждая из которых описывает зависимость уровня полезности индивида от уровня дохода в состоянии s.

Этот переход довольно серьезно влияет на выводы, полученные ранее при рассмотрении модели, описывающей формирование спроса на страхование. Максимум выражения U(L) = Eu = (1-)u_g(W_g)+ u_b(W_b) достигается в иной точке, чем прежде, в условиях независимости функции Бернулли от состояния мира.

Как и прежде в точке оптимума предельная норма замещения должна быть равна отношению цен:

MRS = МU_g /МU_b = (1-)u_g'/u_b'

Как и прежде, на справедливом рынке страхования выполняется условие

(1-)u_g'/ u_b' = (1- р)/ р  u_g'/u_b' = 1

Но, ввиду различия в виде кардиналистских функций, описывающих полезность дохода в различных состояниях : u_g(^.)≠u_b(^.) не будет достигаться совпадения уровней условного дохода в обоих состояниях, соответствующего полному страхованию возможных потерь.

W_g≠ W_b , т.е.W₀ - pq^* ≠ W₀ - L- pq^*+ q^*

q^* ≠ L при p =

Графическая иллюстрация для случая двух возможных состояний s = {gооd,bad} и различающихся функций полезности u_s = {u_g, u_b}

Рис. 2.30.

До сих пор мы, по сути, ограничивались анализом предпочтений индивида на пространстве простых лотерей: выпадение того или иного состояния мира означало получение того или иного выигрыша, а лотереи различались лишь уровнем получаемых призов, при том, что вероятность выпадения того или иного состояния полагалась заданной (некими внешними объективными обстоятельствами, либо ожиданиями самого индивида). Некоторое усложнение модели предполагает учет того обстоятельства, что выпадение того или иного состояния мира может не приводить к гарантированному выигрышу: W_g илиW_b, но определять лишь некоторое вероятностное распределение возможных выигрышей (особое - для каждого состояния мира). Иначе говоря, при каждом состоянии s индивид получает не определенный конечный приз, а сталкивается с некоей вторичной лотереей. Примеры подобного рода ситуаций довольно многочисленны. Состояние здоровья индивида определяет распределение выигрышей( уровня заработной платы), уровень активности правоохранительных органов определяет вероятностное распределение наступления страхового случая(кражи имущества индивида), конъюнктура рынка определяет распределение объемов продаж и т.д.

Обозначим F_s ⁱ - функцию распределения выигрышей в состоянии s в лотерее i

Тем самым игра (лотерея i ) может быть описана вектором функций распределения

L ⁱ = (F₁ ⁱ , F₂ ⁱ , ..., F_S ⁱ ).

Сопоставить такого рода сложные лотереи позволяет введение RCLA ( the reduction of compound lotteries axiom).Таким образом оказывается достаточно, сопоставляя привлекательность такого рода сложных лотерей А и В , сравнить соответствующие им значения ожидаемой полезности

(u_s(W_s)dF^А(W_s)) и (u_s(W_s)dF ^В(W_s))

где Еu_s(W_s ⁱ)=u(W_s) dF_s ⁱ (W_s) - ожидаемая полезность, получаемая индивидом в лотерее i при выпадении состояния s .

Итак, для любых сложных лотерей

А=(F₁^А,F₂^А, ..., F_s^А) и В =(F₁ ^B,F₂^B, ..., F_s^B),

L^А строго предпочитается L ^В, т.е. L^А > L ^Втогда и только тогда, когда

(u_s(W_s)dF_s^А(W_s )) > (u_s(W_s)dF_s ^B(W_s))

Впрочем, сопоставление различных лотерей можно проводить сопоставляя несколько более простые выражения. Для этого нужно переопределить вид функций полезности в s- ом состоянии , т.е. Еu_s(W_s ⁱ), подвергнув их следующим преобразованиям:

Еu_s^*=Еu_s(W_s )/ _s ,

и тогда неравенство Еu_s^*(W_s^А) > Еu_s^*(W_s^B).

может быть заменено на неравенство Еu_s(W_s ^А) > Еu_s(W_s ^B)

и, далее, (u_s(W_s) dF_s^А(W_s)) > (u_s(W_s) dF_s ^B(W_s) )

Иначе говоря, вероятности _s можно не учитывать, ибо взвешивание по одним и тем же вероятностям ожидаемых в s- ых состояниях полезностей не меняет порядка ранжирования величин ожидаемых полезностей сложных лотерей. Этот результат получил название теорема расширенной ожидаемой полезности( the extended expected utility theorem). Разумеется, он справедлив лишь при выполнении неких базовых аксиом, во многом повторяющих предпосылки теоремы Неймана-Моргенштерна. Особого комментария в этой связи заслуживает, пожалуй, лишь формулировка аксиомы независимости. Собственно, принципиальное отличие этой формулировки состоит лишь в том, что в ней идет речь не только о простых, но и о сложных лотереях, все прочее тождественно. Иначе говоря, аксиома предполагает независимость полезности (привлекательности) сложной лотереи А от того, что представляет собой альтернативная сложная лотерея.