1 Неопред БИ 12. 1. Неопределенность информации

• Название: 1. Неопределенность информации
• Дата: 19.09.2018
• Размер: 1.17 Mb.
• Имя файла: 1 Неопред БИ 12.doc
• Тип: Документы; #51096
• страница: 6 из 6

Итак, увеличение числа индивидов повышает ожидаемую полезность каждого за счет сокращения возможных колебаний в уровне дохода( получение индивидом низкого или же высокого дохода в подобном случае менее вероятно, чем прежде, ибо неудача одного может быть смягчена выигрышем другого). Собственно, при сохранении прежнего математического ожидания выигрыша индивиды сталкиваются с меньшим разбросом выигрышей( т.е. менее рискованной игрой или игрой, стохастически второго рода доминирующей исходную). Например, если каждый из двух индивидов может с вероятностями 0.5 выиграть 1 или же не получить ничего, то объединение рисков или переход к лотерее

0.25 о 0 0.5 о 1/2 0.25 о 1 ,

не сказавшись на уровне математического ожидания выигрыша, снизит дисперсию. Для не склонного к риску индивиду подобные изменения влекут за собой возрастание уровня ожидаемой полезности.

Возрастание числа индивидов, объединяющих свои риски, естественно, будет повышать уровень их ожидаемой полезности сходным образом.
Однако следует обратить внимание на то обстоятельство, что в подобной ситуации суммарное богатство варьируется в зависимости от того, какое из состояний реализовалось, и, следовательно, существуют социальные или системные риски. Предоставление полной страховки всем индивидам становится и не возможным и не эффективным.

Невозможным - поскольку для этого нужно было бы иметь сумму вдвое превышающую математическое ожидание выигрыша каждого индивида, т.е.

2 (W₀ - L), а эта величина может оказаться как больше, так и меньше выражения, стоящего в предпоследнем столбце приведенной таблицы.

Неэффективным - поскольку контрактная кривая (в общем случае, т.е. при несклонности к риску обоих контрагентов) более не совпадает с линиями уверенности.

Эффективное распределение риска в контрактах "первого наилучшего".

^{Рассмотрим в качестве примера контракты, заключаемые между агентом и принципалом, и допуская существование системных рисков. Собственно, эти термины( принциал и агент) часто используются в теории контрактов не только для обозначения сторон, заключающих трудовой контракт(хозяин- работник), но и в более широком контексте при описании ситуаций, возникающих в иных, не имеющих отношения к трудовым контрактам, сферах. В подобных случаях речь, как правило идет о различной степени информированности сторон( при этом принципал полагается стороной менее, а агент - более информированной). В будущем мы также будем поступать аналогичным образом. Однако, говоря о контрактах "первого наилучшего", предполагающих симметричность информации, которой располагают стороны, этот контракт заключающие, мы не можем иметь в виду ничего подобного. Тем самым, называя одного агентом, а другого - принципалом, мы лишь следуем необходимости присвоить им некие имена.}

Как уже отмечалось, рассмотрение контрактов "первого наилучшего", не допускает асимметрии информации, не исключая в то же самое время некой неопределенности, неполноты имеющейся информации. Будем полагать, что неопределенность по поводу будущих потерь агентов сводится не к четырем, а всего лишь к двум возможным ситуациям, выроятность выпадение которых принципал и агент, в сущности, могут оценивать по- разному . Соответственно, агент и принципал максимизируют свои ожидаемые полезности

агент max _i ^А u_А (W_i^А )

принципалmax _i^Pu_P(W_i^P)

Обратите внимание, что в данном случае оценки вероятностей выпадения i- го состояния, даваемые принципалом и агентом различны, но функции полезности по-прежнему полагаются не зависящими от выпавшего состояния (state- independent).

Вид контрактной кривой в диаграмме Эджворта (кстати, ее размеры - W₁ х W₂ =(W₁^А + W₁ ^P)х(W₂^А + W₂ ^P)) , как и обычно, может быть получен из условия равенства предельных норм замещения

u_A '(W₁^А )/ u_A '(W₂^А ) = ₁ ^Р u_Р '(W₁ ^P) / ₂ ^Р u_Р '(W₂ ^P)

Для n - мерного случая :

_i ^Au_A '(W_i ^А )/ _j ^Au_A '(W_j ^А ) = _i ^Р u_Р '(W_i ^P) / _j ^Р u_Р '(W_j ^P ) для всех i, j

Однако, разумеется, для подписания контракта необходимо, чтобы ожидаемая полезность, им приносимая, превышала так называемый резервный уровень полезности как для агента, так и для принципала. Речь идет о выполнении так называемых условий участия

_i ^A u_A (W_i^А ) ≥ u_A ⁰

_i ^Рu_Р (W_i^Р) ≥ u_Р ⁰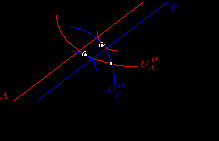

Рис.3.3.а Оптимальное распределение риска в условиях, когдаи принципал и агент не склонны к риску (контрактная кривая лежит ниже линии уверенности - неполное страхование).

Иначе говоря, конечное распределение должно принадлежать участку контрактной кривой между точками B и D. Конкретное же положение точки зависит от того, как распределено влияние: в случае, если вся власть в торге принадлежит принципалу, выбор падет на точку B , а если агенту - то точку D.

Первое (_i ^A u_A (W_i^А) =u_A ⁰) может иметь место когда агенты конкурируют между собой за право подписать контракт, второе (_i ^Рu_Р (W_i^Р) =u_Р ⁰ ) - когда имеет место ситуации common agency (множествo принципалов, конкурируют за агента).

Но в данном случае нас интересует не то, какой именно из точек ядрового распределения BD соответствует конкретный контракт "первого наилучшего", а то, каково оптимальное распределение риска в подобного рода контрактах, или, иначе говоря, каково положение контрактной линии относительно линий уверенности (Вспомните, при негативно коррелированных рисках контрактная кривая совпадает с линиями уверенности, в результате чего индивидам может быть предоставлена полная страховка)

Для того, чтобы разобраться в этом вопросе, предположим, простоты ради, что вероятностные ожидания агента и принципала совпадают. Тогда

u_A '(W_i^А)/ u_A '(W_j ^А) = u_Р '(W_i^Р) / u_Р '(W_j ^Р) или

u_Р '(W_i^Р)/ u_А '(W_i ^А) = u_Р '(W_j ^Р)/ u_А '(W_j ^А) = соnst в любом состоянии

Необяз! Покажем, что несклонность к риску обоих контрагентов будет приводить к построению контракта, распределяющего риск между ними, и более того, оптимальное распределение, которое можно рассматривать как своего рода правило деления общего выигрыша W_i в том или ином состоянии, зависит от степени несклонности агентов к риску. Вернемся к условиям первого порядка и несколько преобразуем их:

u_Р '(W_i ^Р)/ u_А '(W_i^А) = u_Р '(W_j ^Р)/ u_А '(W_j ^А) = соnst =

- u_P '( W_i ^P) +u_A '( W_i^А) = - u_P '(W_i- W_i^A) + u_A '( W_i^А) = 0

Продифференцируем тождество - u_P '(W_i- W_i ^A) + u_A '( W_i^А) = 0 по W_i

- u_P'' [1- dW_i^A/ dW_i] + u_A ''(W_i^А) (dW_i ^А/ dW_i) = 0, где = u_P '( W_i^Р)/ u_A '(W_i^А)

(- u_P''/ u_P ')(1- dW_i^A/ dW_i)+ (u_A''/ u_A ') (dW_i ^А/ dW_i) = 0

- u_P''/ u_P ' = R_P ; - u_A''/ u_A ' = R_{A ;}

R_P (1- dW_i^A/ dW_i)+ R_A (dW_i^A/ dW_i)= 0

(dW_i ^A/ dW_i) = R_P /(R_P + R_A)

Эта производная убывает по R_A , но возрастает поR_Р , что означает, что чем более несклонен к риску агент и чем менее несклонен к риску принципал, тем незначительнее варьирование доли агента А в зависимости от уровня W_i.

_{Постоянство коэффициентов абсолютной несклонности к риску} R_A и R_{Р (}т.е. принадлежность функций полезности и агента и принципала к классу САRA функций) приводящее к постоянству (dW_i ^A/ dW_i) означает, по сути, оптимальность заключения линейных контрактов W_i ^A(W_i) = с + bW_i . Для функций полезности с постоянной относительной несклонностью к риску, т.е. СRRA функций линейность такого рода контрактов не нуждается в комментарии. Необходимо только отметить, что линейные контракты будут оптимальными, функции полезности обоих контрагентов принадлежат к одному и тому же подклассу СRRA функций.

Итак, если информация симметрична - линейные контракты оптимaльны лишь для САRA и СRRA функций, объединяемых в класс НАRA или LRT функций, о котором говорилось ранее.
Нейтральность принципала к риску : МRS^Р=_i ^Р/ _j ^Р

Если вероятностные ожидания совпадают, то нейтральность принципала к риску предполагает равный уровень оплаты не склонного к риску агента в любом из возможных состояний. Иначе говоря , в контракте первого наилучшего риск полностью возлагается на сторону, нейтральную к риску, т.е. W_i ^A = W_j ^A .

Действительно, условия первого порядка будут в оговоренном случае могут быть приведены к следующему виду :

= 1 / u '_A (W_i ^A)) = 1 / u '_A (W_j ^A)) = соnstant W_i ^A = W_j ^A.

Графическая иллюстрация для ситуации, в которой возможны лишь два состояния: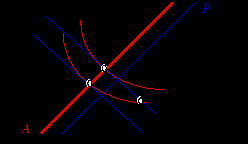

Рис.3.1.б Оптимальное распределение риска в условиях, когда принципал нейтрален к нему .

Если принципал нейтрален к риску (например, u(W) = W), то он смирится с колебаниями в уровне богатства, вызванными действием случайных факторов (разумеется, ожидаемая полезность при этом должна быть не ниже резервной), в то время как агент , переложив весь риск на принципала, будет получать фиксированный доход. Нейтральность принципала к риску (при несклонности к нему агента) обусловливает возложение всего риска именно на принципала (например, установление агенту фиксированной заработной платы), в то время как нейтральность к риску агента предполагает получение фиксированного дохода не склонным к риску принципалом ( сдача предприятия в аренду, франшиза).

Однако, представляется ли убедительной гипотеза о нейтральности к риску одной из сторон? Весь следующий раздел будет посвящен обсуждению именно правомерности принятия этой гипотезы, базирующейся, в свою очередь, на предположениях

• значительного количества покупателей страховки;

• статистической независимости рисков.

Однако эти предпосылки создают лишь возможность для того, чтобы фирмы устанавливали "справедливые" цены за страхование, вынудить же их на этот шаг может лишь конкуренция на рынке. Достаточно сложно отнести рынок страхования к категории конкурентных рынков. Скорее речь может идти либо о рынках, на которых фирмы, ввязавшись в ценовую войну, конкурируют по Бертрану, либо просто о так называемых состязательных (contestable) рынках, не огражденных барьерами и открытых для входа конкурирующих фирм. Последнее вынуждает фирмы, реализующие свою продукцию на этих рынках, устанавливать цены на уровне, близком к конкурентному.

1 В частности, Даниэль Бернулли, воспользовавшись в качестве кардиналистской функции полезности потребителя, зависящей от величины выигрыша W_i , логарифмической функцией

u(W_i) = ln(W_i),

получил более чем разумную величину 1,39 - как цену , которую потребитель готов заплатить за право участия в этой игре.

1 Пол Шумейкер Модель ожидаемой полезности. Альманах THESIS Риск , случайность, неопределенность. 1994, № 5,с. с.35-36.