финанс матем. 1. общие понятия

• Название: 1. общие понятия
• Дата: 16.09.2022
• Размер: 3 Mb.
• Имя файла: финанс матем.docx
• Тип: Документы; #680939
• страница: 4 из 5

FV = PV(1 + i)ⁿ / (1 + _τ)ⁿ.

Наращение осуществляется по простым или сложным процентам, но инфляция всегда оценивается по сложному проценту.

Поскольку ставка доходности (i) является фактором роста денег, то находится в числителе формулы, а показатель инфляции (τ) является фактором их обесценивания, поэтому находится в знаменателе формулы.

Пример. Пусть ежемесячный уровень инфляции 2,5 %. Определить ожидаемый уровень инфляции за квартал. Решение. Индекс инфляции за месяц

J = 1 + _τ = 1 + 0,025 = 1,025. τ

Индекс инфляции за квартал, т. е. за три месяца

J = (1 + _τ )³ = 1,025³ = 1,077. τ

Уровень инфляции за квартал

τ = J – 1 = 1,077 – 1 = 0,077. τ

Следовательно, ожидаемый квартальный уровень инфляции составит 7,7 %.

Показатели финансовой операции могут быть представлены как:

• 
  номинальные, т. е. рассчитанные в текущих ценах; 
  
• 
  реальные, т. е. учитывающие влияние инфляции и рассчитанные в сопоставимых ценах базисного периода. 
  

Пример. Определить реальные результаты вкладной операции для суммы 5 000 руб., размещенной на полгода под 8 % годовых, если ежемесячный уровень инфляции составляет 2 %.

Решение. Наращенная сумма вклада

FV = PV(1 + ni) = 5 000 (1 + 0,5 · 0,08) = 5 200,00 руб.

Индекс инфляции за срок хранения вклада составит J = (1 + 0,02)⁶ = 1,126. τ

Реальная сумма вклада FV = 5 200 / 1,126 = 4 618,11 руб. τ

Следовательно, наращенная величина по своей покупательной способности с учетом инфляции будет соответствовать сумме 4 618,11 руб., т. е. меньше первоначальной суммы.

5.2 Методы учета инфляции в финансовых расчетах 

Владельцы денег не могут мириться с их обесцениванием в результате инфляции и предпринимают различные попытки компенсации потерь от снижения их покупательной способности.

Наиболее распространенным методом является индексация ставки процентов, по которой производится наращение, поскольку:

• 
  Ø если уровень инфляции равен ставке начисляемых процентов ( _τ = i), то реального роста денежных сумм не будет, т. к. наращение будет полностью поглощаться инфляцией;
  
• 
  Ø если уровень инфляции выше уровня процентной ставки (_ > i),то происходит «проедание» капитала, и реальная наращенная сумма будет меньше первоначальной денежной суммы;
  
• 
  Ø если уровень инфляции ниже процентной ставки (_ < i), то это будет соответствовать росту реальной денежной суммы.
  

В связи с этим вводится понятие номинальная ставка процента, т. е. ставки с поправкой на инфляцию (i ). τ

Общая формула для определения простой ставки процентов, компенсирующей ожидаемую инфляцию, имеет следующий вид: i = [(1 + ni) · J_ - 1] : n,τ

где i – простая ставка процентов, характеризующая требуемую реальную доходность финансовой операции (нетто-ставка); i_ – процентная ставка с поправкой на инфляцию. Пример. Банк выдал клиенту кредит на один год в размере 20 тыс. руб. по ставке 6 % годовых. Уровень инфляции за год составил 18 %. Определить с учетом инфляции реальную ставку процентов по кредиту, погашаемую сумму и сумму процентов за кредит. Решение. Номинальная наращенная сумма

FV = PV(1 + ni) = 20 000 (1 + 0,06) = 21 200,00 руб.

Номинальные начисленные проценты

I = FV – PV = 21 200 – 20 000 = 1 200,00 руб.

Реальная наращенная сумма FV = FV / (1 + _) = 21 200 / 1,18 = 17 966,10 руб. τ

Реальные проценты I = FV – PV = 17 966,10 – 20 000 = –2 033,90 руб. τ τ

Таким образом, получен убыток от данной финансовой операции в размере 2 033,90 руб.

Ставка по кредиту с учетом инфляции должна быть равна i = [(1 + ni) · I – 1] : n = (1,06 · 1,18 – 1) / 1 = 0,2508. τ     τ

Наращенная сумма

FV = PV (1 + ni) = 20 000 (1 + 0,2508) = 25 016,00 руб.

Доход банка

I = FV – PV = 25 016 – 20 000 = 5 016,00 руб.

Реальный доход банка I = FV – PV = 25 016 / 1,18 – 20 000 = 1 200,00 руб. τ   τ

Реальная доходность финансовой операции

i = I / PV = 1 200 / 20 000 = 0,06. τ

Таким образом, чтобы обеспечить доходность в размере 6 % годовых, ставка по кредиту с учетом инфляции должна соответствовать 25,1 % годовым.

Годовая ставка сложных процентов, обеспечивающая реальную доходность кредитной операции, определяется по формуле



ТЕМА 6 КРЕДИТНЫЕ РАСЧЕТЫ

 

6.1 Планирование погашения долга

6.1.1. Погашение долга единовременным платежом

Количественный анализ долгосрочной задолженности (займа) применяется для достижения сбалансированности, т. е. адекватности его параметров принятым условиям финансового соглашения, путем планирования погашения долга.

Планирование погашения долга заключается в определении периодических расходов, связанных с займом, – такие расходы называются обслуживанием долга. Разовая сумма обслуживания долга – срочная уплата, в которую входят:

• 
  текущие процентные платежи;
  
• 
  средства для погашения (амортизации) основной суммы долга.
  

Размеры срочных уплат зависят от условий займа:

• 
  срока;
  
• 
  наличия и продолжительности льготного периода;
  
• 
  уровня процентной ставки;
  
• 
  способа погашения основной суммы долга и выплаты процентов.
  

Для кредитной схемы в качестве исходных параметров выступают величина займа (D), срок его погашения (n), процент по кредиту (i), под который выдаются деньги, и поток платежей по выплате долга (Y_t).

Рассмотрим различные способы погашения задолженности, поскольку от выбора способа погашения стоимость кредита (сумма выплачиваемых процентов) будет различной. Здесь возможны два варианта:

а) погашение единовременным платежом, т. е. возврат всей суммы в оговоренный

срок;

б) погашение долга в рассрочку, т. е. частями.

6.1.1.1. Погашение основной суммы долга единовременным платежом в конце срока с постоянной выплатой процентов

Рассмотрим погашение единовременным платежом. В простейшем случае кредит погашается единым платежом в конце срока: 

Y = D · (1 + i)ⁿ,

где Y – срочная уплата, D – сумма долга. Этот платеж, как наращенная сумма долга, состоит из двух частей:

–  возврат основной суммы долга (D);

–  выплата процентов по долгу (I), где I = D · (1 + i)ⁿ – D.

В финансовой практике встречаются случаи, когда у кредитора возникает необходимость вернуть часть денег досрочно. В таких случаях возникает риск невозврата, поскольку требуемой суммы на такой момент времени может и не быть.

При значительной сумме долга разовый платеж требует создания так называемого фонда погашения путем периодических взносов. Фонд погашения аккумулирует денежные средства, направленные на погашение задолженности. Наиболее эффективно размещение фонда погашения с начислением на взносы процентов, например на специальном счете в банке. Нетрудно заметить, что такие платежи по своей сути являются финансовой рентой (аннуитетом), поэтому задача сводится к определению одного из параметров финансовой ренты – члена ренты.

Здесь возможно два варианта.

Первый – выплата процентов по мере их начисления, когда основная сумма денег возвращается в конце срока займа. 



где D – первоначальная сумма долга; q – ставка процентов по условиям займа; s_{n; i} – коэффициент наращения финансовой ренты; n – срок долга в годах; i – ставка процентов при создании фонда погашения.

Здесь фигурируют две ставки процентов: i – определяет скорость роста суммы фонда погашения; q – сумму выплачиваемых за заем процентов.

Пример. Долг 100 тыс. долларов выдан под 10 % годовых на три года, с ежегодной выплатой процентов по долгу. Для погашения суммы долга единовременным платежом создается фонд, куда ежегодно вносятся равные суммы, на которые начисляются проценты по ставке 11 %. Найти ежегодные расходы должника. Решение. Ежегодные расходы должника составляют величину срочной уплаты Y = I + R,

I = D · q = 100 000 · 0,1 = 10 000 долларов,







Таким образом, из приведенной таблицы видно, что ежегодные расходы по обслуживанию долга составят 39 921,31 долларов, что в целом за три года составит сумму 119 763,93 долларов, причем выплата процентов за три года – 30 000 долларов, а на погашение основного долга в размере 100 000 долларов приходится всего лишь 89 763,93 долларов, т. е. 10 236,07 долларов является набежавшими процентами на размещенные средства в фонде погашения.

Таким образом, создание фонда погашения является необходимым элементом составления плана погашения долга, т. к. позволяет не только снизить риск невозврата денежных средств, но и сократить расходы по обслуживанию суммы долга.

6.1.1.2. Погашение основной суммы долга и процентов по нему единовременным платежом в конце срока ссуды

Второй вариант погашения долга единовременным платежом состоит в выплате процентов одновременно с погашением долга: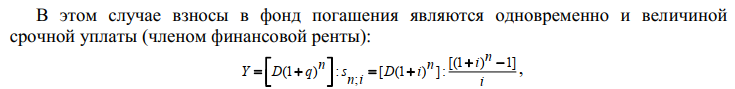





где D – первоначальная сумма долга; q – ставка процентов по условиям займа; s_{n; i} – коэффициент наращения финансовой ренты; n – срок долга в годах; i – ставка процентов при создании погасительного фонда.

Пример. Рассмотрим предыдущий пример, изменив условия: погашение единовременным платежом как суммы основного долга, так и выплаты процентов. Решение. Величина срочной уплаты равна

Y = [D · (1 + q)ⁿ] : S_{n; i} = 100 000 · (1 + 0,11) · 3 : 3,3421000 = 39 825,26 долларов.

Таким образом, величина ежегодных расходов по обслуживанию долга составит 39 825,26 долларов, что несколько меньше аналогичного показателя в предыдущем примере, следовательно, меньше и общая сумма расходов по обслуживанию долга, составляющая величину 119 475,78 долларов.

Для более наглядного представления плана погашения долга здесь также необходимо составление таблицы.





Как видно из таблицы, происходит ежегодное увеличение суммы долга за счет присоединения к нему процентов, поэтому к концу срока долг возрастет до 133 100 долларов, из которых выплата процентов составит 33 100 долларов. Однако за счет увеличения размера взносов в погасительный фонд общая величина обслуживания долга уменьшается.

6.1.2. Погашение долга в рассрочку

В практике финансовой деятельности долг часто погашается в рассрочку, т. е. распределенными во времени платежами. При погашении основной суммы долга частями его текущее значение будет уменьшаться, и, следовательно, сумма процентных платежей также будет уменьшаться.

Погашение долга частями также может осуществляться различными способами. В зависимости от преследуемых интересов стороны могут выбирать различные, удобные для них режимы в виде постоянных или переменных финансовых рент, а также нерегулярных потоков платежей.

6.1.2.1. Погашение основной суммы долга равными частями

Одним из вариантов погашения долга в рассрочку является погашение основной суммы долга равными частями. При этом величина погашения долга определяется следующим образом: d_t = D : n = const,

где d_t – величина погашения основной суммы долга; D – первоначальная сумма долга; n – срок долга в годах; t – номер года; t = 1, 2, …, n.

Проценты начисляются на уменьшаемую сумму основного долга

I_t = D_t· q,

где D_t – остаток долга на начало очередного года, q – ставка процентов, начисляемых на сумму долга.

Тогда размер срочной уплаты можно представить как сумму процентов и сумму погашения долга:

Y_t = I_t + d_t,

где Y_t – срочная уплата на конец текущего года.

Пример. Сумма 100 тыс. долларов выдана под 10 % годовых на три года. Определить величину срочной уплаты при погашении основной суммы долга равными ежегодными частями. Решение. Величина суммы погашения долга равна

d_t = D : n = 100 000 : 3 = 33 333,33 доллара.

Поскольку величина срочной уплаты при таком способе погашения долга меняется из года в год, то в этом случае без построения плана погашения долга в виде таблицы просто не обойтись.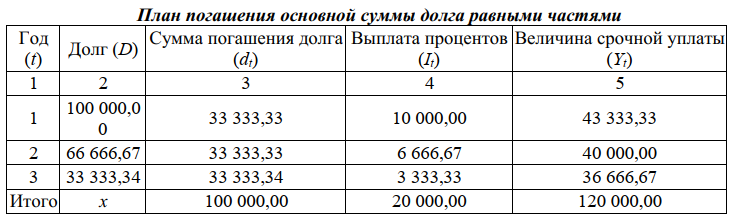 



Таким образом, общие расходы по обслуживанию долга составили 120 тыс. долларов, из которых 20 тыс. долларов составляют проценты, а 100 тыс. долларов – погашение основной суммы долга.^[1]

6.1.2.2. Погашение долга и процентов по нему равными суммами в течение срока ссуды

Долг также можно погашать в рассрочку равными срочными уплатами, которые включают в себя как погашение основной суммы долга, так и величину процентов по нему:

Y_t = I_t + d_t = const.

При погашении долга в рассрочку величина долга систематически убывает, что приводит к уменьшению процентов и, соответственно, увеличению сумм, идущих на погашение долга, – это так называемое прогрессивное погашение.

Поскольку срочные уплаты равны, то их последовательность представляет собой финансовую ренту, современное значение которой должно быть равно сумме долга.

По формуле для определения размера платежа постоянной годовой финансовой ренты с выплатами в конце периода размер срочной уплаты равен: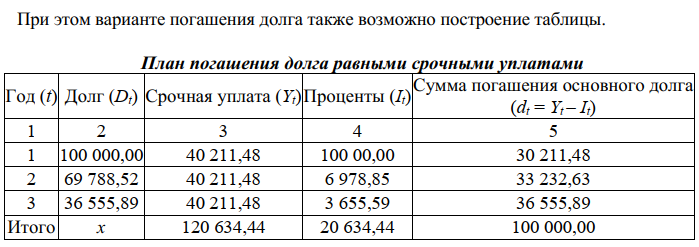





Таким образом, общие расходы по обслуживанию долга составляют 120 634,44 долларов, из которых 100 тыс. долларов идут на погашение долга, а 20 634,44 долларов – проценты. В таблице наглядно представлено распределение суммы срочной уплаты на выплату процентов и непосредственное погашение долга.

6.1.3. Потребительский кредит

Частным случаем погашения долга равными срочными уплатами является потребительский кредит, при котором проценты начисляются сразу на всю сумму кредита, а сумма задолженности равномерно погашается на протяжении всего срока кредита. Проценты в потребительском кредите начисляются сразу на всю сумму долга по простой ставке:

I = D · n · i.

Тогда общая сумма расходов по погашению кредита складывается из выплаты процентов и суммы основного долга:

ΣY_t = D + I.

Следовательно, размер срочной уплаты определяется по формуле

ΣY_t = (D + I) : (n · m),

где n – срок кредита в годах; m – количество взносов в течение года.

Пример. Потребительский кредит на сумму 5 тыс. руб. открыт на два года по ставке

25 % годовых. Погашение кредита равными взносами ежеквартально. Определить стоимость кредита и размер ежеквартальных взносов. Решение. Стоимость кредита – это проценты, которые равны I = D · n · i = 5 000 · 2 · 0,25 = 2 500 рублей.

Общая сумма расходов по обслуживанию кредита равна

ΣY_t = D + I = 5 000 + 2 500 = 7 500 рублей.

Ежеквартальные взносы составят величину

ΣY_t = (D + I) : (n · m) = 7 500 : 2 · 4 = 937,50 рублей.

Таким образом, ежеквартальные взносы в размере 937,50 рублей позволяют выплатить сумму долга и выплатить проценты.

Если бы использовалось прогрессивное погашение, т. е. начисление процентов на остаток долга, то это было бы заметно дешевле для должника.

Расчленение величины срочной уплаты в потребительском кредите на процентные платежи и погашение основной суммы долга в мировой практике называется «методом 78». Это связано с тем, что для потребительского кредита сроком 12 месяцев и ежемесячным погашением сумма порядковых номеров месяцев будет равна 78, что и дало название такому методу начисления процентов.

Это правило можно обобщить для n лет и m платежей в году: N = m · n [(m · n + 1) : 2],

где N – сумма последовательных номеров выплат.

Отсюда очень легко расчленить срочную уплату на процентные платежи и сумму погашения основного долга:

Y_t = I_t + d_t,

где I_t – процентный платеж; d_t – сумма погашения основного долга. Тогда величина процентного платежа определяется следующим образом:

I_t = I · (t / N),

а сумма погашения основного долга как разница срочной уплаты и процентных выплат

R_t = Y_t – I_t.

Рассмотрим предыдущий пример, расчленив срочную уплату на составляющие элементы, все данные представив в виде таблицы.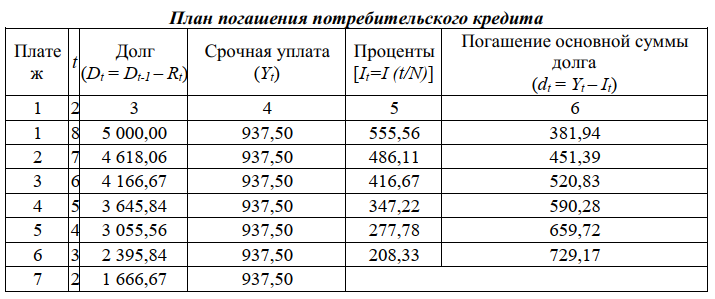



ТЕМА 7 ОЦЕНКА ИНВЕСТИЦИОННЫХ ПРОЦЕССОВ

 

7.1 Особенности инвестиционных процессов как объекта финансовой математики

Инвестиции – это долгосрочные финансовые вложения экономических ресурсов с целью создания и получения выгоды в будущем, которая должна быть выше начальной величины вложений.

Инвестиционный процесс – это последовательность связанных инвестиций, растянутых во времени, отдача от которых также распределена во времени (рис. 7.1). Этот процесс характеризуется двусторонним потоком платежей, где отрицательные члены потока являются вложениями денежных средств в инвестиционный проект, а положительные члены потока – доходы от инвестированных средств.



Принято различать:

• 
  финансовые инвестиции; 
  
• 
  реальные инвестиции; 
  
• 
  инвестиции в нематериальные активы. 
  

Финансовые инвестиции – вложение денежных средств в ценные бумаги; реальные инвестиции – вложения в основной капитал и прирост запасов; инвестиции в нематериальные активы – вложения в развитие научных исследований, повышение квалификации работников, приобретение лицензий и прав.

Реализация инвестиционных проектов требует отказа от денежных средств сегодня в пользу получения дохода в будущем, поэтому любой инвестиционный проект требует анализа и оценки.

Оценивая эффективность инвестиционных проектов, следует учитывать и степень риска – здесь, как правило, выделяют два вида риска: предпринимательский и финансовый.

Предпринимательский риск – риск, связанный с деятельностью конкретного бизнеса. Финансовый риск связан с изменениями рыночной ставки дохода на капитал.

Для упрощения исследования эффективности инвестиций предполагается, что необходимая норма прибыли задана и одинакова для всех инвестиционных проектов и для любого из рассматриваемых проектов степень риска одинакова.

Различают простые (статические) и усложненные (динамические) методы. Простые методы традиционно использовались в социалистической экономике и отвечали действующим тогда условиям хозяйствования. В рыночных условиях используются методы, основанные на теории временной стоимости денег, которые устранили недостаток ранее действующих методик.

Важнейшая задача анализа инвестиционных проектов – расчет будущих денежных потоков, возникающих при реализации проекта, но не прибыли. Анализ инвестиционных проектов основан на исследовании доходов и расходов, выраженных в форме денежных потоков, но не на изменениях, вызванных условностями бухгалтерского учета.

В данной главе рассматриваются только методы и показатели эффективности инвестиций, основанные на принципе дисконтирования.

При анализе потоков платежей используются обобщающие показатели:

• 
  наращенная стоимость;
  
• 
  приведенная стоимость;
  
• 
  норма доходности.
  

Эти показатели уже рассматривались в теоретической части, но для инвестиционных процессов они приобретают свою специфику.

7.2 Показатели эффекта и эффективности инвестиционных проектов

7.2.1. Чистый приведенный доход

Поскольку денежные средства распределены во времени, то и здесь фактор времени играет важную роль.

При оценке инвестиционных проектов используется метод расчета чистого приведенного дохода, который предусматривает дисконтирование денежных потоков: все доходы и затраты приводятся к одному моменту времени.

Центральным показателем в рассматриваемом методе является показатель NPV (net present value) – текущая стоимость денежных потоков за вычетом текущей стоимости денежных оттоков. Это обобщенный конечный результат инвестиционной деятельности в абсолютном измерении.

При разовой инвестиции расчет чистого приведенного дохода можно представить следующим выражением: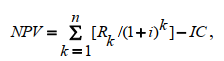



где R_k – годовые денежные поступления в течение n лет, k = 1, 2, …, n;  IC – стартовые инвестиции; i – ставка дисконтирования.

Важным моментом является выбор ставки дисконтирования, которая должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке. Для определения эффективности инвестиционного проекта отдельной фирмой в качестве ставки дисконтирования используется средневзвешенная цена капитала, используемого фирмой для финансирования данного инвестиционного проекта.

Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение нескольких лет (m), то формула для расчета модифицируется:



Показатель NPV является абсолютным приростом, поскольку оценивает, на сколько приведенный доход перекрывает приведенные затраты:

• 
  при NPV > 0 проект следует принять;
  
• 
  при NPV < 0 проект не принимается,
  
• 
  при NPV = 0 проект не имеет ни прибыли, ни убытков.
  

Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала фирмы в случае принятия данного проекта.

Одно из важных свойств данного критерия, что показатель NPV различных проектов можно суммировать, поскольку он аддитивен во времени. Это позволяет использовать его при анализе оптимальности инвестиционного портфеля.

Пример. Фирма рассматривает целесообразность инвестиционного проекта, стоимость которого составляет 210 тыс. долларов. По прогнозам, ежегодные поступления составят 55 тыс. долларов. Проект рассчитан на пять лет. Необходимая норма прибыли составляет 8 %. Следует ли принять этот проект?

Решение. Чистая стоимость проекта равна^[1]

NPV = 55 000 (1,08)^–1 + 55 000 (1,08)^–2 + 55 000 (1,08)^–3 + 55 000 (1,08)^–4 + + 55 000 (1,08)^–5 – 210 000 = 50 926 + 42 867 + 39 692 + 36 751 + 34 029 – 210 000 =  = 204 265 – 210 000 = –5 735 долларов.

Поскольку величина чистой текущей стоимости –5 735 долларов, т. е. NPV < 0, то проект не может быть принят.

Как правило, основываются на том, что величина NPV находится на начало реализации инвестиционного проекта, однако можно определять эту величину на момент завершения процесса вложений или на иной момент времени.

Напомним, что ставка дисконтирования – результат выбора, субъективного суждения. Кроме того, при высоком уровне ставки отдаленные платежи будут оказывать на величину NPV малое влияние, поэтому варианты, отличающиеся по продолжительности периодов отдачи, могут оказаться равноценными по конечному экономическому эффекту.

7.2.2. Срок окупаемости

Для анализа инвестиций применяют и такой показатель, как срок окупаемости (payback period method) – продолжительность времени, в течение которого дисконтированные на момент завершения инвестиций прогнозируемые денежные поступления равны сумме инвестиций. Иными словами – это сумма лет, необходимых для возмещения стартовых инвестиций:



Срок окупаемости проекта k_ок = 3 + 54 / 458 = 3,12.

Таким образом, период, реально необходимый для возмещения инвестированной сумы, составит 3,12 года, или три года и 44 дня.

Если доходы можно представить в виде аннуитета, то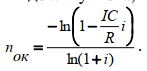



Срок окупаемости существует, если не нарушаются определенные соотношения между поступлениями и размером инвестиций. При ежегодных постоянных

поступлениях это соотношение имеет вид

R_k < IC · i,

т. е. не всякий уровень дохода при прочих равных условиях приводит к окупаемости инвестиций.

7.2.3. Внутренняя норма доходности

При анализе эффективности инвестиционных проектов широко используется показатель внутренней нормы доходности (IRR – internal rate of return) – это ставка дисконтирования, приравнивающая сумму приведенных доходов от инвестиционного проекта к величине инвестиций, т. е. вложения окупаются, но не приносят прибыль. Величина этой ставки полностью определяется «внутренними» условиями, характеризующими инвестиционный проект.

Применение данного метода сводится к последовательной итерации (повторению) нахождения дисконтирующего множителя, пока не будет обеспечено равенство NPV = 0.

Выбираются два значения коэффициента дисконтирования, при которых функция

NPV меняет свой знак, и используют формулу

IRR = i₁ + NPV(i₁) / [NPV(i₁) – NPV(i₂)] · (i₂ – i₁). Инвестор сравнивает полученное значение IRR со ставкой привлеченных финансовых ресурсов (CC – Cost of Capital):

–  если IRR > CC, то проект можно принять; 

–  если IRR < СС, проект отвергается; 

–  IRR = СС – проект имеет нулевую прибыль. 

Пример. Рассчитать внутреннюю ставку доходности по проекту, где затраты составляют 1 200 тыс. руб., а доходы 50; 200; 450; 500 и 600 тыс. руб.

Решение. Расчет по ставке 5 %:

NPV = 47 619 + 181 406 + 388 767 + 411 351 + 470 116 – 1 200 000 = 299 259. Поскольку NPV > 0, то новая ставка дисконтирования должна быть больше 5 %.

Расчет по ставке 15 %:

NPV = 43 478 + 151 229 + 295 882 + 285 877 + 298 306 – 1 200 000 = –125 228.

Вычисляем внутреннюю ставку доходности

IRR = 5 + [299 259 / [299 259 – (–125 228)]] · (15 – 5) = 12,05. Внутренняя норма доходности проекта равна 12,05 %.

Точность вычисления обратна величине интервала между выбираемыми процентными ставками, поэтому для уточнения величины процентной ставки длина интервала принимается за 1 %.

Пример. Уточнить величину ставки для предыдущего примера.

Решение. Для процентной ставки 11 %:

NPV = 45 045 + 162 324 + 329 036 + 329 365 + 356 071 – 1 200 000 = 21 841.

Для процентной ставки 12 %:

NPV = 44 643 + 159 439 + 320 301 + 317 759 + 340 456 – 1 200 000 = –17 402.

Уточненная величина

IRR = 11 + [21 841 / [21 841 – (–17 402)]] · (12 – 11) = 11,56.

Ставка 11,56 % является верхним пределом процентной ставки, по которой фирма может окупить кредит для финансирования инвестиционного проекта.

[1] Задача решается с использованием формулы современной величины обычной ренты.