финанс матем. 1. общие понятия

• Название: 1. общие понятия
• Дата: 16.09.2022
• Размер: 3 Mb.
• Имя файла: финанс матем.docx
• Тип: Документы; #680939
• страница: 3 из 5

или D = FV · t / T · d = 5 000 · 90 / 360 · 0,08 = 100 руб.

Следовательно, предъявитель векселя получит сумму 4 900 руб., а банк при наступлении срока векселя реализует дисконт в размере 100 руб.:

- по сложной учетной ставке PV = FV · (1 – d)ⁿ.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т. к. учетная ставка каждый раз применяется к уменьшаемой на величину дисконта величине.

Пример. Определить величину суммы, выдаваемую заемщику, если он обязуется вернуть ее через два года в размере 55 тыс. руб. Банк определяет свой доход с использованием годовой учетной ставки 30 %.

Решение. Используя формулу дисконтирования по сложной учетной ставке, определяем

PV = FV · (1 – d)ⁿ = 55 000 · (1 – 0,3)² = 26 950 руб. Заемщик может получить ссуду в размере 26 950 руб., а через два года вернет 55 тыс.

руб.

Объединение платежей можно производить и на основе учетной ставки, например, при консолидировании векселей. В этом случае сумма консолидированного платежа рассчитывается по следующей формуле:

FV_oб = ΣFV_j· (1 – d · t_j) ^–1,

где t_j – интервал времени между сроками векселей.

Пример. Вексель на сумму 10 тыс. руб. со сроком погашения 10.06, а также вексель на сумму 20 тыс. руб. со сроком погашения 01.08 заменяются одним с продлением срока до 01.10. При объединении векселей применяется учетная ставка 25 %. Определить сумму консолидированного векселя.

Решение. Для использования формулы консолидированного платежа необходимо определить срок пролонгации векселей:

t₁ = 21 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 1 (октябрь) – 1 = 113 дней, t₂ = 31 (август) + 30 (сентябрь) + 1(октябрь) – 1 = 61 день.

Тогда, сумма консолидированного векселя

FV_o = ΣFV_j · (1 – d · t_j) ^–1 = 10 000 · (1 – 113 / 360 · 0,25) ^–1 + 20 000 · (1 – 61 / 360 · 0,25) ^–1 = 31 736 руб.

Таким образом, сумма консолидированного векселя с датой погашения 01.10 составит 31 736 руб.

В том случае, когда учету подлежит долговое обязательство, по которому предусматривается начисление процентов, происходит совмещение начисления процентов по процентной ставке и дисконтирования по учетной ставке:

PV₂ = PV₁· (1 + n₁·i ) · (1 – n₂·d ),

где PV₁ – первоначальная сумма долга;

PV₂ – сумма, получаемая при учете обязательства;

n₁ – общий срок платежного обязательства;

n₂ – срок от момента учета до погашения.

Пример. Обязательство уплатить через 100 дней сумму долга в размере 50 тыс. руб. с начисляемыми на нее точными процентами по ставке 40 % было учтено за 25 дней до срока погашения по учетной ставке 25 %. Определить сумму, полученную при учете обязательства.

Решение. Следует обратить внимание на различие временных баз, используемых при наращении и учете:

PV₂ = PV₁· (1 + n₁·i) · (1 – n₂·d ) = 50 000 · (1 + 100 / 365 · 0,4) · (1 – 25 / 360 · 0,25) = = 54 516 руб.

Следовательно, сумма, получаемая при учете данного обязательства, составит 54 516 руб.

Основные зависимости и параметры простых и сложных финансовых операций при начислении процентов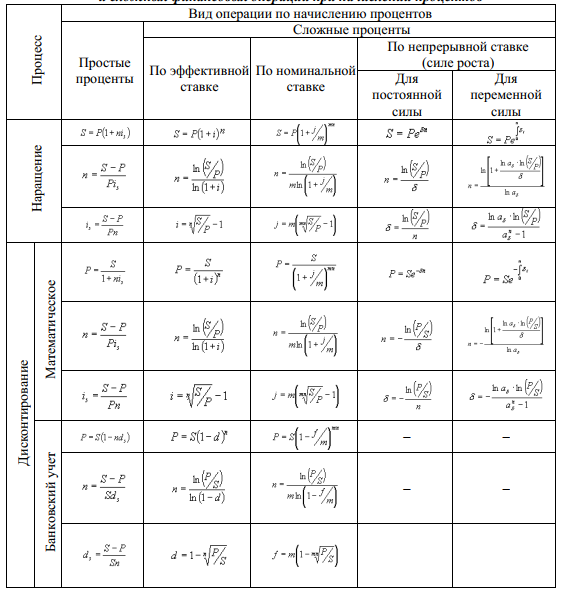



ТЕМА 4 ПОТОКИ ПЛАТЕЖЕЙ И ФИНАНСОВЫЕ РЕНТЫ

 

4.1 Сущность потока платежей и основные категории

До сих пор мы рассматривали случаи финансовых операций, состоящих из отдельного разового платежа, например получение и погашение долгосрочной ссуды. Вместе с тем погашение такой ссуды возможно не только единовременным платежом, но множеством распределенных во времени выплат. В финансовой литературе ряд распределенных во времени выплат и поступлений называется потоком платежей.

Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с ценными бумагами, в управлении финансами предприятий, при осуществлении инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке недвижимости, выборе альтернативных вариантов финансовых операций и т. п.

Члены потока могут быть как положительными величинами (поступления), так и отрицательными величинами (выплатами), а временные интервалы между членами такого потока могут быть равными и неравными.

Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом.

При рассмотрении финансовой ренты используются основные категории:

• 
  член ренты (R) – величина каждого отдельного платежа; 
  
• 
  период ренты (t) – временной интервал между членами ренты; 
  
• 
  срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода; 
  
• 
  процентная ставка (i) – ставка, используемая при наращении платежей, из которых и виды потоков платежей состоит рента. 
  

Поскольку условия финансовых сделок весьма разнообразны, в основу классификации финансовых рент положены различные качественные признаки.

В зависимости от периода продолжительности ренты выделяют:

• 
  годовую ренту, которую представляют собой ежегодные платежи, т. е. период ренты равен 1 году; 
  
• 
  срочную ренту, при которой период ренты может быть как более, так и менее года. 
  

По числу начислений процентов различают: 

• 
  ренты с начислением 1 раз в год; • ренты с начислением m раз в год;
  
• 
  непрерывное начисление. 
  

По величине членов ренты могут быть: 

–      постоянные ренты, где величина каждого отдельного платежа постоянна, т. е. рента с равными членами; 

–      переменные ренты, где величина платежа варьируется, т. е. рента с неравными членами. 

По числу членов ренты они бывают: 

• 
  с конечным числом членов (ограниченные ренты), когда число членов ренты конечно и заранее известно; 
  
• 
  с бесконечным числом (вечные ренты), когда число ее членов заранее не известно. 
  

По вероятности выплаты ренты делятся на:

§ верные ренты, которые подлежат безусловной выплате, т. е. не зависят не от каких условий, например погашение кредита;  § условные ренты, которые зависят от наступления некоторого случайного события.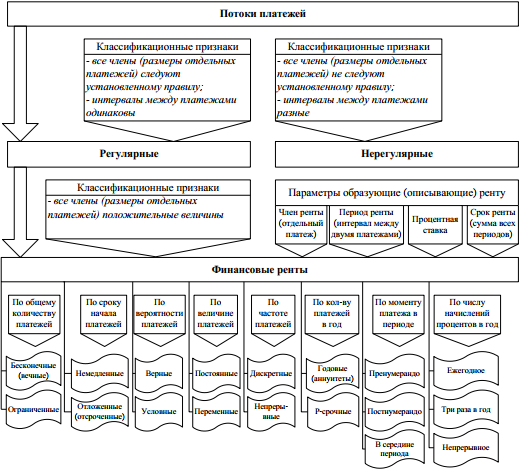 



По методу выплаты платежей выделяют:

• 
  обычные ренты, которые на практике встречаются чаще всего, – с выплатой платежа в конце периода ренты (постнумерандо); 
  
• 
  ренты, с выплатой в начале периода ренты (пренумерандо).
  

 

4.2 Обобщающие характеристики финансовых потоков

Обобщающими характеристиками финансовых потоков являются:

– наращенная сумма;  – современная величина потока платежей. 

 

4.2.1. Наращенная величина аннуитета

Получатели поступлений оценивают свой доход суммарной величиной за полный срок действия платежа – разумеется, с учетом временной неравноценности денег.

Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т. п.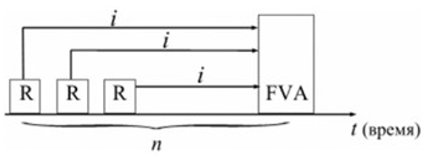



Наращенные отдельные платежи представляют собой члены геометрической прогрессии с первым членом равным R и множителем равным (1 + i).

Рассмотрим определение наращенной суммы на примере наиболее простого случая – годовой постоянной обычной ренты:



где FVA – наращенная сумма ренты; R – размер члена ренты, т. е. размер очередного платежа; i – годовая процентная ставка, по которой на платежи начисляются сложные проценты; n – срок ренты в годах; s _n;i – коэффициент наращения ренты.

Пример. На счет в банке в течение пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30 %. Определить сумму процентов, которую банк выплатит владельцу счета.

Решение. Поскольку период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, – значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т. е. конечно – следовательно, ограниченная рента; выплаты носят безусловный характер – таким образом, это верная рента.

Сумма всех взносов с начисленными процентами будет равна



Можно определить наращенную сумму постоянной ренты, воспользовавшись финансовыми таблицами (приложение 4), содержащими коэффициенты наращения ренты:

FVA = R · s_{5 ; 30} = 500 · 9,0431 = 4 521,55 руб.

Сумма взносов в течение пять лет составит

P = n · R = 5 · 500 = 2 500 руб.

Следовательно, сумма начисленных процентов будет равна

I = FVA – P = 4 521,55 – 2 500 = 2 021,55 руб.

Таким образом, доход владельца счета за пять лет составит 2 021,55 руб.

Для овладения методами финансовой математики важно запоминание не столько формул, сколько общих принципов расчета.

Для определения наращенной суммы на конец рассматриваемого периода последовательно присоединяются промежуточные результаты наращения к очередному платежу.

Рассмотрим поэтапное решение предыдущего примера.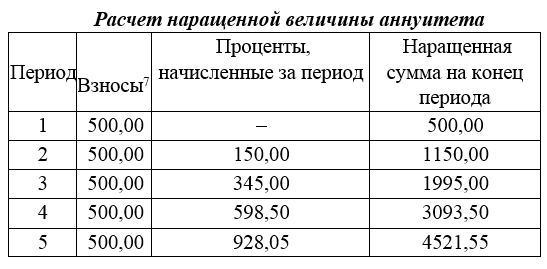



Таким образом, получается такая же сумма, как и по формуле наращения аннуитета.

Однако рассматриваемая формула используется только при начислении процентов один раз в год, а возможны случаи и неоднократного начисления процентов в течение года, тогда используют следующую формулу: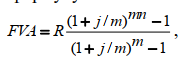



где j – номинальная ставка процентов.

Пример. Рассмотрим предыдущую задачу, изменив условия: проценты начисляются поквартально.

Решение. В этом случае будет рента с начислением процентов четыре раза в год, а общее количество начислений составит 20 раз. Отсюда сумма всех взносов с начисленными на них процентами будет равна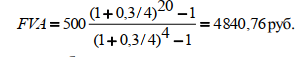



Сумма начисленных процентов будет равна

I = FVA – P = 4 840,76 – 2 500,00 = 2 340,76 руб.

Как видим, переход от годового начисления процентов к ежеквартальному начислению заметно увеличил как наращенную сумму, так и сумму процентов.

Бывают случаи, когда рентные платежи вносятся несколько раз в год равными суммами (срочная рента), а начисление процентов производится только раз в году. Тогда наращенная величина ренты будет определяться по формуле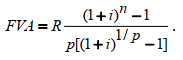



p[(1 i)^1/ p _1]

Также нередки случаи, когда рентные платежи вносятся несколько раз в году и начисление процентов также происходит несколько раз в год, но число рентных платежей    не      равно         числу         периодов   начисления         процентов, т. е. 

p ≠ m. Тогда формула, по которой можно определить наращенную величину финансовой ренты, примет вид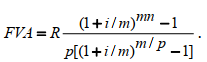



На практике большее распространение получил поток постнумерандо, поскольку согласно общим принципам учета принято подводить итоги и оценивать финансовый результат операции или иного действия по окончании очередного отчетного периода. Что же касается поступления денежных средств в счет оплаты, то на практике они чаще всего распределены во времени неравномерно, и поэтому для удобства все поступления относят к концу периода, что позволяет использовать формализованные алгоритмы оценки.

Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.

Рента пренумерандо отличается от обычной ренты числом периодов начисления процентов. Поэтому наращенная сумма ренты пренумерандо будет больше наращенной суммы обычной ренты в (1 + i) раз.

Для годовой ренты пренумерандо с начислением процентом один раз в год формула примет вид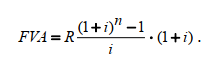



Для годовой ренты пренумерандо с начислением процентов несколько раз в год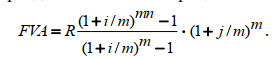



4.2.2. Современная (текущая) величина аннуитета

Помимо наращенной суммы обобщающей характеристикой потока платежей является современная величина. Современная (текущая) величина потока платежей RVA (или, при другом обозначении А, – капитализированная или приведенная величина) – это сумма платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов. Это важнейшая характеристика финансового анализа, т. к. является основой для измерения эффективности различных финансово-кредитных операций, сравнения условий контрактов и т. п. Данная характеристика показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые начислялись бы установленные проценты в течение всего срока, можно было бы получить указанную наращенную сумму.

В этом случае реализуется схема дисконтирования: все элементы с помощью дисконтных множителей приведены к одному моменту времени, что позволяет их суммировать.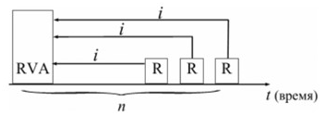



В простейшем случае, для обычной годовой ренты с выплатами в конце каждого года, когда момент оценки совпадает с началом ренты, современная величина финансовой ренты равна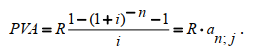 



Дробь в формуле – коэффициент приведения ренты (a_n;i), значения которого табулированы для широкого круга значений, поскольку зависят от ставки процентов (i) и от числа лет (n) (приложение 5).

Пример. Определить по данным примера современную величину ренты.

Решение. Современная величина ренты составит



Таким образом, все производимые в будущем платежи оцениваются в настоящий момент в размере 1 217,78 руб.

Рассмотрим расчет современной величины ренты для различных ее видов:

годовая рента с начислением процентов несколько раз в год:



4.3 Определение основных параметров аннуитета

 

Последовательные платежи в виде постоянной обычной годовой ренты определяются основными параметрами:

• 
  R – размер платежа;
  
• 
  n – срок ренты в годах;
  
• 
  i – годовая ставка процентов.
  

Однако при разработке условий финансовой операции могут возникать ситуации, когда заданной величиной являются одна из двух обобщающих характеристик и неполный набор параметров ренты. В таких случаях находят недостающий параметр.

При определении члена ренты возможны два варианта, зависящие от того, какая величина является исходной:

а) наращенная сумма. Если сумма долга определена на какой-либо момент в будущем (FVA), тогда величину последующих взносов в течение n лет при начислении на них процентов по ставке i можно определить по формуле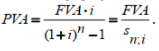 



Пример. Для покупки автомобиля через пять лет потребуется 50 тыс. руб. Определите размер ежегодных взносов, вносимых в конце каждого года в банк, который начисляет проценты по ставке 40 %.

Решение. В данном случае известна наращенная величина постоянной финансовой ренты, поэтому размер ежегодных взносов будет равен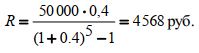



Таким образом, чтобы накопить на счете необходимую сумму для покупки автомобиля, следует в конце каждого года в течение пяти лет откладывать 4 568 руб.;

б) современная величина финансовой ренты. Тогда, исходя из ставки процента и срока ренты, разовый платеж находится по формуле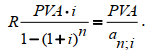



предоставлена в долг на пять лет под 8 % годовых.

Определить ежегодную сумму погашения долга.

Решение. Известна современная величина долга, отсюда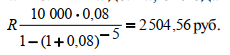



Таким образом, ежегодно необходимо будет возвращать сумму 2 504,56 руб.

Можно произвести проверку: сумма долга с начисленными на нее процентами к концу пятого года будет составлять:

FV = 10 000 · (1 + 0,08)⁵ = 14 693,28 руб.

Наращенная сумма для потока платежей размером 2 504,56 руб. составит: 



Следовательно, величина члена финансовой ренты определена верно. Незначительное расхождение вызвано округлением расчетов.

Современная величина ренты пренумерандо рассчитывается путем умножения современной величины обычной ренты на соответствующий множитель наращения.

 

4.4 Оценка некоторых видов аннуитета

 

4.4.1. Бессрочный аннуитет

Если денежные поступления осуществляются достаточно длительное время и их число заранее не может быть известно, то такой поток называется бессрочным аннуитетом, или вечной рентой. В этом случае определение будущей величины такого аннуитета не имеет смысла.

Для данного вида финансовой ренты имеет смысл только характеристика современной величины потока платежей. Поток, даже с неограниченным числом платежей, все же имеет конечную приведенную стоимость, поскольку с финансовой точки зрения деньги, поступающие через много лет, сейчас практически ничего не стоят.

Для бессрочного аннуитета постнумерандо формула современной величины принимает следующий вид: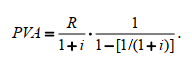



При больших сроках аннуитета и большом уровне процентной ставки для определения приведенной величины срочного аннуитета можно пользоваться формулой бессрочного аннуитета, поскольку полученный приблизительный результат не слишком будет отличаться от точного значения, т. к. при сроке более 40–50 лет коэффициенты дисконтирования аннуитета незначительно отличаются друг от друга.

Приведенная стоимость бессрочного аннуитета пренумерандо в общем виде определяется из приведенной стоимости бессрочного аннуитета постнумерандо, скорректированного на коэффициент (1 + i), т. е. отличается на величину первого платежа.

 

4.4.2. Непрерывный аннуитет

Если промежутки между последовательными поступлениями являются бесконечно малой величиной, то такой аннуитет считают непрерывным, т. е. денежные поступления происходят непрерывно с постоянной интенсивностью.

При начислении непрерывных процентов для получения формул определения наращенной или современной величины потока платежей необходимо перейти к пределу, откуда:

наращенная величина потока платежей



4.5 Нерегулярные потоки платежей

 

В финансовых операциях возможны ситуации, когда величина платежа либо увеличивается, либо уменьшается с течением времени, например под влиянием инфляции. В таких случаях говорят о нерегулярных потоках платежей.

Нерегулярные потоки платежей характеризуются присутствием хотя бы одного нерегулярного параметра: периода ренты или размера платежа.

Для получения их обобщающих характеристик требуется прямой счет, т. е. вычисление соответствующих характеристик по каждому платежу и последующему их суммированию.

Однако в ряде случаев можно применять следующую формулу:



Таким образом, наращенная сумма потока А через пять лет составит 1 325,21 рублей. Наращение суммы для потока В: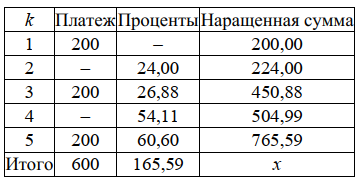 



Для потока В наращенная сумма через пять лет составит 765,59 рублей.

Если воспользуемся вышеприведенной формулой, то:

–  для потока А наращенная величина составит

FVA = 100 · (1 + 0,12)⁴ + 200 · (1 + 0,12)³ + 200 · (1 + 0,12)² + 200 · (1 + 0,12)¹ + 300 = = 1 325,22 руб.;

–  для потока В наращенная величина составит

FVA = 200 · (1 + 0,12)⁴ + 200 · (1 + 0,12)² + 200 = 765,58 руб.

Таким образом, расчет по формуле для нерегулярных потоков платежей дает такой же

результат, как и прямой счет.

ТЕМА 5. ИНФЛЯЦИЯ В ФИНАНСОВО-КОММЕРЧЕСКИХ РАСЧЕТАХ

 

5.1 Сущность инфляции и необходимость ее учета в количественном анализе

 

Инфляция – это экономическое явление, которое возникает вследствие целого комплекса как политических, так и социально-экономических событий. Уровень инфляции выступает обобщающим показателем финансово-экономического положения страны. 

Инфляция – устойчивый рост среднего уровня цен на товары и услуги в экономике. 

Инфляция – многомерное и многоаспектное явление, которое можно классифицировать на основе различных критериев. Внешним проявлением инфляции является повышение общего уровня цен, т. е. совокупный рост цен на товары и услуги в течение длительного времени. Соответственно, на денежную единицу приходится меньше товаров, т. е. деньги обесцениваются.

Если наблюдается общее снижение цен, то происходит дефляция.

Темпы инфляции определяются с помощью индекса инфляции – относительного показателя, характеризующего среднее изменения уровня цен некоторого фиксированного набора товаров и услуг за данный период времени.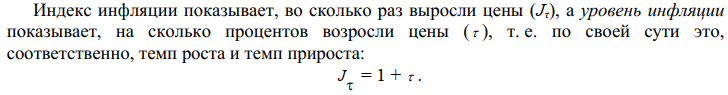



Для оценки уровня инфляции используется система индексов цен.

Индекс потребительских цен (ИПЦ) – это показатель международной статистики, регулярно использующийся практически во всех странах мира (CPI – Consumer Price Index), который характеризует динамику затрат на постоянный набор товаров и услуг за счет ценностного фактора.

Индекс потребительских цен дает достаточно обобщенную характеристику инфляции, так как потребление является завершающим этапом в создании валового продукта, и здесь находят свое отражение все предыдущие стадии производства.

Расчет ИПЦ в России осуществляется за каждый месяц и нарастающим итогом с начала года (к декабрю прошлого года).

Отечественные исследователи часто расценивают уровень инфляции как темп прироста потребительских цен:



В зависимости от уровня инфляции в год выделяют:

• 
  нормальную (ползучую) – от 3 % до 10 %; 
  
• 
  галопирующую – от 10 % до 100 %; 
  
• 
  гиперинфляцию – свыше 50 % в месяц. 
  

Еще одним важным показателем международной статистики, оценивающим инфляцию, является дефлятор валового внутреннего продукта, который характеризует изменение стоимостного объема ВВП за счет его ценностного фактора. Дефлятор ВВП также дает обобщенную характеристику инфляции, поскольку характеризует движение цен на потребительском рынке, а также на рынке инвестиционных товаров и услуг. Для характеристики инфляции могут применяться и другие показатели: размер эмиссий, сокращение товарных запасов и т. п. 

Инфляция противодействует повышению стоимости денег, обесценивая их. Графически это представлено на рис. 9.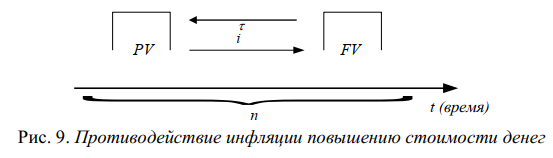 



Вследствие начисления процентов происходит увеличение денежных сумм, но их стоимость под влиянием инфляции уменьшается. Поскольку каждая денежная единица обесценивается вследствие инфляции, то в дальнейшем обесцениваются уже обесцененные деньги. Таким образом, формула для исчисления наращенной суммы с учетом влияния инфляции принимает следующий вид: