1. Определение функции нескольких переменных. Основные понятия
 Скачать 7.57 Mb.
|
|
52. Закон больших чисел: неравенство Чебышева. Под «законом больших чисел» в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным. В основе- неравенство Чебышева: Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше чем : 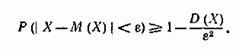 Справедливо для дискретных и непрерывных с.в. 53. Теорема Чебышева. Пусть имеется бесконечная последовательность независимых случайных величин  с одним и тем же математическим ожиданием и дисперсиями, ограниченными одной и той же постоянной С:  Тогда каково бы ни было положительное число  вероятность события стремится к единице. 54. Теорема Бернулли. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. 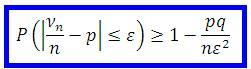 55. Понятие о центральной предельной теореме Ляпунова. Распределение суммы большого числа независимых случайных величин при весьма общих условиях близко к нормальному распределению. Известно, что нормально распределенные случайные величины широко распределены на практике. Объяснение этому было дано А.М.Ляпуновым в центральной предельной теореме: если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному. 56. Генеральная совокупность и выборка: основные определения и понятия. Математическая статистика – наука, занимающаяся разработкой методов получения, описания и обработки опытных данных с целью изучения закономерностей случайных массовых явлений. Задачи математической статистики:
Пусть изучается некоторый количественный признак x. Тогда под генеральной совокупностью понимается множество всех его возможных значений. Для изучения свойств данного признака из генеральной совокупности случайным образом отбирается часть элементов вариантами Xi, которые образуют выборочную совокупность или выборку. Число элементов совокупности называется ее объектом n. Выборки: 1) повторная- выборка, при которой отобранный объект(перед отбором следующего0 возвращается в генеральную совокупность. 2) бесповторная- выборка, при которой отобранный объект в генеральную совокупность возвращается. Чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо чтобы выборка была репрезентативной9представительной) В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект генеральной совокупности должен иметь одинаковую вероятность попасть в выборку. Если объект генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается. Перечень вариант, расположенный в возрастающем порядке называется вариационным рядом. Число наблюдений данной варианты называется ее частотой ni, а отношение частоты ni к объекту выборки n-относительной частоты wi. 57. Статистическое распределение. Полигон и гистограмма. Статистическое распределение называется соответствие между вариантами и их частотами или относительными частотами. (варианта – часть отбираемых элементов из генеральной совокупности. частота – число наблюдений данной варианты, относительная частота – отношение частоты к объёму выборки). Для графической иллюстрации статистического распределения используют полигон частот или гистограмму. Полигон частот – ломаная линия, соединяющая точки с координатами (x,n(на графике f)). 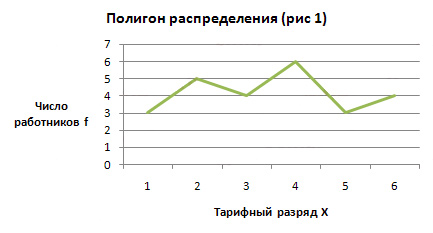 Если значения признака выражены в виде интервалов, то такой ряд называется интервальным. Гистограммой называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной ��i, а высота i-го прямоугольника равна отношению частоты попадания значения х в i-й интервал к его длине (плотность частоты). 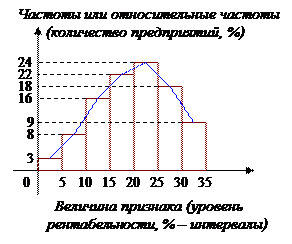 58. Точечные и интервальные статистические оценки и их свойства. Точечные оценки-оценки, выраженные одним числом. Пусть изучается дискретная генеральная совокупность относительно количественного признака 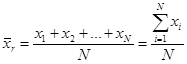х:
 =M(х)Если значения 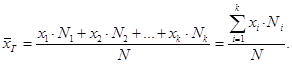 имеют соответственно частоты  , причем  , то =M(х)Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n. Выборочным средним называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака выборки объема n различны, то:  .Если значения признака имеют частоты соответственно, причем , то:  .Выборочная средняя применяется для оценки неизвестного математического ожидания случайной величины. Она является несмещённой и состоятельной оценки математического ожидания. Генеральной дисперсией Dr называется среднее арифметическое квадратов отклонения значений признака х генеральной совокупности от генеральной средней. 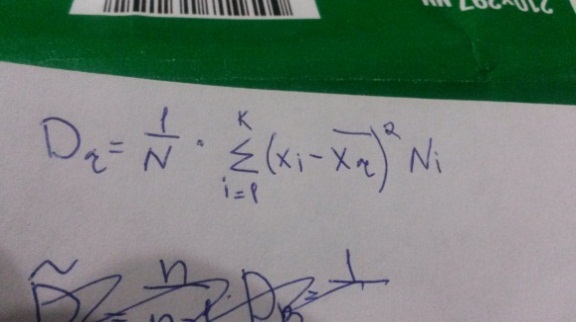 Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонения наблюдаемых значений признака Х от выборочной средней  Выборочная дисперсия является состоятельной, но смещенной оценкой дисперсии. Несмещенной и состоятельной оценкой дисперсии является исправленная выборочная дисперсия  При малом объеме выборки (n<=30) пользуются исправленной выборочной дисперсией, при больших n безразлично какой пользоваться. Для практических расчетов выборочной дисперсии используют формулу: 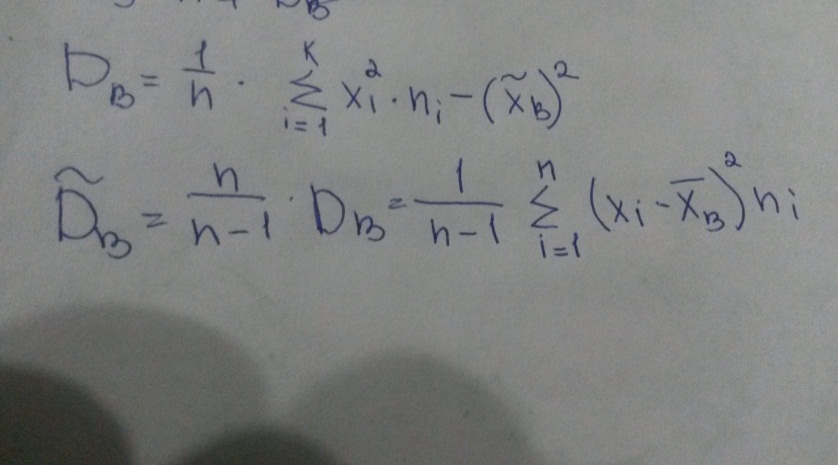 Среднее квадратичное отклонение равно корню из выборочной дисперсии Интервальные оценки параметров распределения определяется двумя числами – концами интервала. Интервал (Õ1; Õ2) называется доверительным для параметра О с доверительной вероятностью (надёжностью) y (0 P(Õ1 59. Доверительный интервал для оценки неизвестного математического ожидания нормального распределения генеральной совокупности при известном среднем квадратическом отклонении вычисляется по формуле  где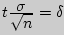 
1.
определение
функции нескольких
переменных.
основные понятия.
если
каждой паре
независимых
друг от друга
чисел (х,у) из
некоторого
множества по
какому-либо
правилу ставится
в соответствие
одно значение
переменной
z,
то она называется
функцией
двух переменных.
- точность оценки, - объем выборки, - выборочное среднее, - аргумент функции Лапласа, при котором |
где α-надежность.
