|
|
1. Определение функции нескольких переменных. Основные понятия
Объем тела вращения:
y=f(x), f(x) – непрерывна на [a;b]. Если соответственно ей криволинейную трапецию вращать вокруг оси Ох, то получим тело вращения. Каждое сечение тела плоскостью х=const – это круг радиуса R=│y(x)│
Vx=π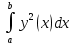

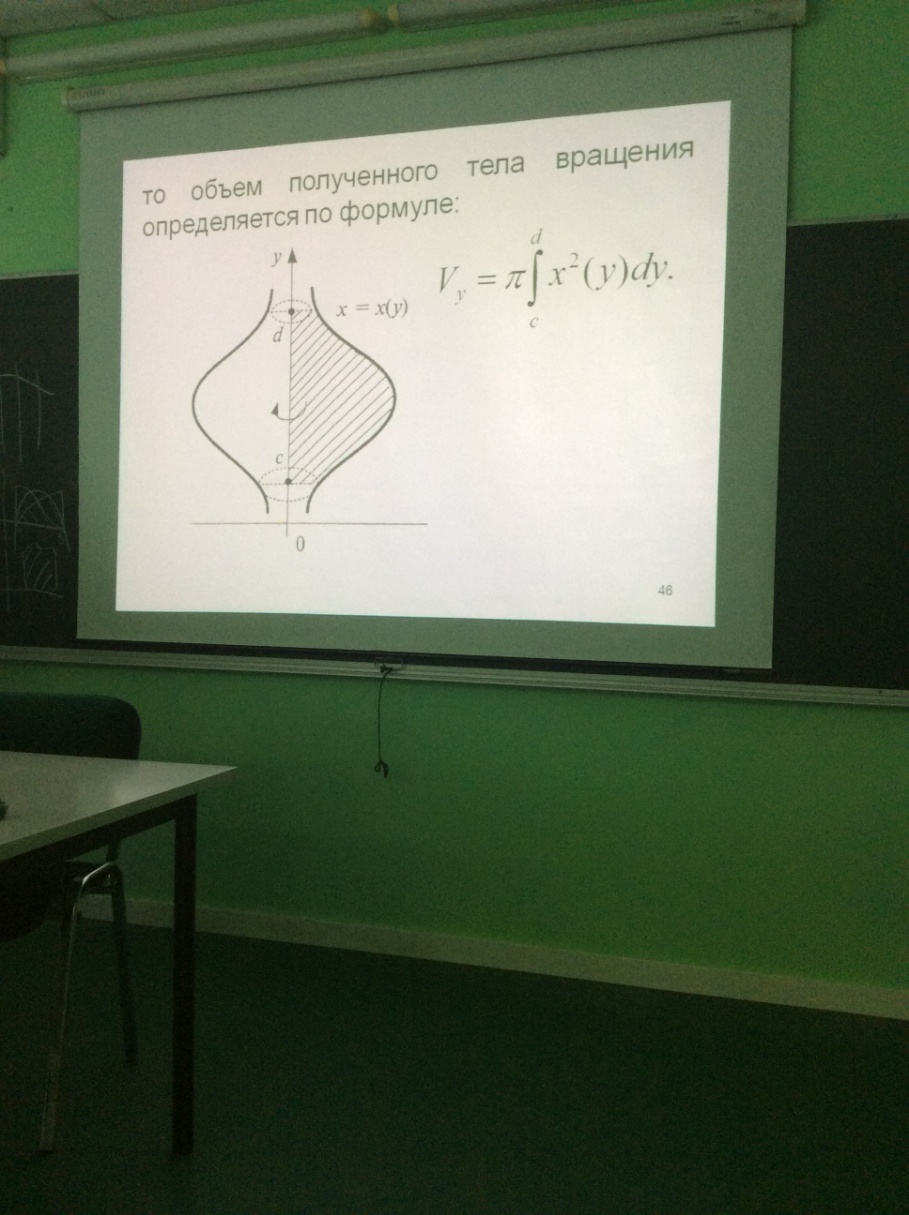
Если криволинейную трапецию вращать вокруг оси Оy, то объем тела вращения по формуле:
Vy=π
14. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА
Пусть f(x) определена и непрерывна на 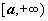 . Тогда она непрерывна на любом отрезке [a; b]. . Тогда она непрерывна на любом отрезке [a; b].
Если существует конечный предел 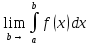 , то это предел – несобственный интеграл от f(x) на , то это предел – несобственный интеграл от f(x) на
[a; ].
Обозначается: 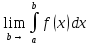 = =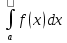
Если этот предел существует и конечен, то несобственный интеграл сходится.
Если этот предел не существует или бесконечен, то несобственный интеграл расходится.
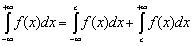
Это справедливо, если интегралы существуют.
Геометрический смысл: Если f(x) ≥0, то несобственный интеграл выражает площадь неограниченной области, заключенной между линиями y=f(x), x=a и осью абсцисс.
15. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА
Если в точке х=С f(x) либо не определена, либо разрывна, то:
=
Если интеграл существует, то сходится.
Если интеграл не существует, то расходится
Если в точке a=x функция терпит разрыв, то:
=
Если f(x) терпит разрыв в точке b, то на [a; c]:
= +
Точек в отрезке может быть несколько.
Если сходятся все интегралы, входящие в сумму, о сходится суммарный интеграл.
16. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. ОСНОВНЫЕ ПОНЯТИЯ.
Дифференциальное уравнение (ДУ) – уравнение, связывающее независимую переменную х, функцию у = у(х) и ее производные и дифференциалы.
F(x,y,y’,y’’…) = 0
ДУ содержи только производные и дифференциалы, а функцию у и переменную х – не обязательно.
Если ДУ имеет одну независимую переменную, то оно обыкновенное ДУ
Если ДУ имеет больше двух независимых переменных, то это ДУ частных производных
Порядок ДУ – наивысший порядок производных, входящих в него.
Общее решение – такая дифференцируемая функция у = у(х, С), которая при подстановке в уравнение обращает его в тождество.
y'=y, y = cex
Иногда Ф(х,у,С)=0, которое не разрешается относительно У. Тогда это общий интеграл, а не решение.
Решение у=у(х, СО) получается из общего решения при определенном значении С – частное решение.
Задача Коши – нахождение частного решения ДУ вида у = у(х,Со), удовлетворяющего начальным условиям у(хо) = уо.
Интегральная кривая – график у = у(х) решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.
17. Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
Дифференциальным уравнением первого порядка называется соотношение, связывающее независимую переменную, функцию и ее первую производную. Общий вид: F(x, y, y`) = 0
Уравнение разрешимое относительно y`, называется дифференциальным уравнением первого порядка, разрешенное относительно производной. y` = f(x, y).
Дифференциальное уравнение первого порядка с разделяющимися переменными.
Диф. уравн. 1-го порядка - уравнением с разделяющимися переменными, если оно пожжет быть представлено в виде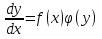 , где , где 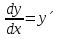
Для решения дифференциального уравнения искомую функцию y представим в виде произведения двух множителей y = uv, где u – некоторое ненулевое решение соответствующего однородного уравнения. u` + p(x) = 0, а v-новая неизвестная функция. Так как y` = vu` + uv`, то подставляя … получим v[u`+p(x)u] + uv` = q(x) →uv`=q(x)
18. Однородные функции и однородное дифференциальное уравнение 1-го порядка.
Опр. Многочлен P(x,y) = ∑aijxiyj называется однородным степени n, если все его члены имеют один и тот же порядок n, т.е. для каждого члена имеем I + j = n
Если аргументы x,y однородного многочлена степени n заменить на пропорциональные величины λx и λy, то в результате этот многочлен увеличится на n-степень коэффициента пропорциональности λ.
Опр. Функция P(x,y) называется однородной степени n относительно своих аргументов х и у, если для любого числа λ (кроме 0) имеет место: Р(λх, λу) = λ”P(x,y)
Р. Однородным дифф. уравнением называется уравнение вида М(х,у)dx + N(x,y)dy = 0, где M(x,y) и N(x,у) – однородные функции одной и той же степени.
Опр. Дифф. уравнение, которое можно преобразовать к виду y’ = ϕ(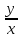 ) называется однородным. ) называется однородным.
С помощью подстановки u = 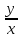 или u=yx, где u(x) – новая неизвестная функция, данное уравнение приводится к уравнению с разделяющимися переменными. или u=yx, где u(x) – новая неизвестная функция, данное уравнение приводится к уравнению с разделяющимися переменными.
Действительно, y = ux, тогда y’ = u’x ≠ ux’
Подставим в y’ = ϕ(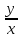 ), получим: u’x + ux’ = ϕu, u’x + u = ϕ(x), и таким образом получим уравнение с разд.переменными относительно u: ), получим: u’x + ux’ = ϕu, u’x + u = ϕ(x), и таким образом получим уравнение с разд.переменными относительно u:
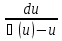 = = 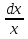 ; ; 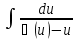 = = 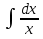 + C + C
Или: 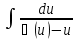 = ln |x| + C = ln |x| + ln |C| = ln |xC| = ln |x| + C = ln |x| + ln |C| = ln |xC|
После этого осуществляется подстановка u = 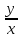 и в результате получаем общее решение однородного дифф.уравнения. и в результате получаем общее решение однородного дифф.уравнения.
19. Линейные дифференциальные уравнения 1-го порядка и уравнение Бернулли.
Уравнение вида y’ + Р(х)у = Q(x), где Р(х) и Q(x) – известные функции от х, линейные относительно функции у и её производной y’, называется линейным дифференциальным уравнением первого порядка.
Если q(x)=0, уравнение называется линейным однородным уравнением. q(x)=0 – линейное неоднородное уравнение.
Линейное уравнение приводится к двум уравнениям с разделяющимися переменными при помощи подстановки у = u*v, где u = u(х) и v = v(x) – некоторые вспомогательные непрерывные функции.
Итак, у = u*v, у’ = u’*v + u * v’ (1),
тогда исходное уравнение перепишем в виде: u’*v + u * v’ + Р(х)*v = Q(x) (2).
Так как неизвестная функция у ищется в виде произведения двух функций, то одна из них может быть выбрана произвольно, другая – определяться уравнением (2).
Выберем так, чтобы v’ + Р(х)*v = 0 (3). Для этого достаточно, чтобы v(x) была частным решением уравнения (3) (при С = 0). Найдём это решение:
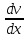 = -v*P(x) ; = -v*P(x) ; 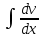 = - = -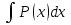 ; ln |v| = - ; ln |v| = -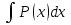 ; v = ; v =  (4) (4)
Подставляя функцию (4) в уравнение (2), получим второе уравнение с разделяющимися переменными, из которого находим функцию u(x):
u’ *  = Q(x) ; du = Q(x) * = Q(x) ; du = Q(x) *  ; u = ; u = 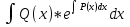 + C (5) + C (5)
Окончательно получаем:
y(x) = u(x)*v(x) =  *( *( 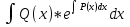 + C) + C)
Уравнение Бернулли: y’ + y = x* y3
Данное уравнение имеет вид: y’ + Р(х)*у = y’’ * Q(x), где Р(х) и Q(x) – непрерывные функции.
Если n = 0, то уравнение Бернулли становится линейным дифф.уравнением. Если n = 1, уравнение преобразуется в уравнение с разделяющимися переменными.
В общем случае, когда n ≠ 0, 1, ур. Бернулли сводится к линейному дифф.уравнению с помощью подстановки: z = y1-n
Новое дифф.уравнение для ф-ции z(x) имеет вид: z' + (1-n)P(x)z = (1-n)Q(x) и может быть решено теми же способами, что и линейные дифф.уравнения 1-ого порядка.
20. Дифференциальные уравнения высших порядков.
Рассмотрим уравнение, не содержащие функцию в явном виде:
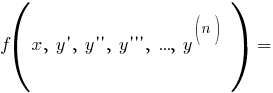
|
(1)
|
Порядок этого уравнения понижается на единицу с помощью подстановки:
Действительно, тогда:
...
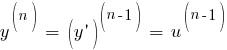
И мы получили уравнение, в котором порядок понижен на единицу:
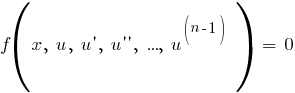
Дифф. уравнения порядка выше второго имеют вид 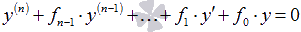 и и  , где , где 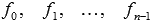 - действительные числа, а функция f(x) непрерывна на интервале интегрирования X. - действительные числа, а функция f(x) непрерывна на интервале интегрирования X.
Аналитически решить такие уравнения далеко не всегда возможно и обычно используют приближенные методы. Однако в некоторых случаях возможно отыскать общее решение.
Теорема.
Общим решением y0 линейного однородного дифференциального уравнения 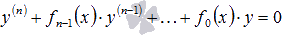 на интервале X с непрерывными коэффициентами на интервале X с непрерывными коэффициентами 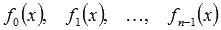 на X является линейная комбинация n линейно независимых частных решений ЛОДУ на X является линейная комбинация n линейно независимых частных решений ЛОДУ 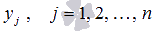 с произвольными постоянными коэффициентами с произвольными постоянными коэффициентами 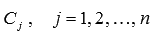 , то есть , то есть 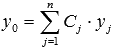 . .
Теорема.
Общее решение y линейного неоднородного дифференциального
уравнения 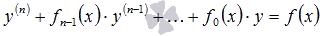 на интервале X с непрерывными на том же на интервале X с непрерывными на том же
промежутке X коэффициентами 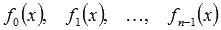 и функцией f(x)представляет собой сумму и функцией f(x)представляет собой сумму 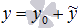 , ,
где y0 - общее решение соответствующего ЛОДУ 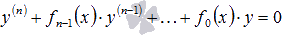 , а - какое-нибудь частное решение исходного ЛНДУ. , а - какое-нибудь частное решение исходного ЛНДУ.
Таким образом, общее решение линейного неоднородного дифференциального уравнения с постоянными
коэффициентами  ищем в виде ищем в виде 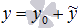 , где - какое-нибудь , где - какое-нибудь
его частное решение, а 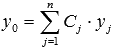 – общее решение соответствующего однородного дифференциального – общее решение соответствующего однородного дифференциального
уравнения 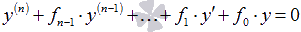 . .
21. Испытания и события. Виды событий. Примеры.
Испытание – создание определённого комплекса условий для совершения событий. Пример: бросание игральной кости
Событие – появление\непоявление того или иного исхода испытания; результат испытания. Пример: выпадение числа 2
Случайное событие – событие, которое может произойти или не произойти при данном испытании. Пример: выпадение числа, большего чем 5
Достоверное – событие, которое неизбежно происходит при данном испытании. Пример: выпадение числа, большего или равного 1
Возможное – событие, которое может произойти при данном испытании. Пример: выпадение числа 6
Невозможное – событие, которое не может произойти при данном испытании. Пример: выпадение числа 7
Пусть А – некоторое событие. Под событием, противоположным ему, будем понимать событие, состоящее в ненаступлении события А. Обозначение: Ᾱ. Пример: А – выпадение числа 2, Ᾱ - выпадение любого другого числа
События А и В несовместны, если наступление одного из них исключает наступление другого в одном и том же испытании. Пример: выпадение при одном броске чисел 1 и 3.
События А и В называются совместными, если они могут появиться в одном испытании. Пример: выпадение при одном броске числа, большего, чем 2, и числа 4.
22. Полная группа событий. Примеры.
Полная группа событий – события A, B, C, D, …, L, которые принято считать единственно возможными, если в результате каждого испытания хотя бы одно из них обязательно наступит. Пример: выпадение на игральной кости числа 1, числа 2, 3, 4, 5, 6.
23. Частота события. Статистическое определение вероятности.
Пусть проведено n испытаний, причём событие А наступило m раз. Такое отношение m:n является частотой наступления события А.
Опр. Вероятность случайного события – связанное с данным событием постоянное число, вокруг которого колеблется частота наступления этого события в длинных сериях испытаний.
Вероятность вычисляется до опыта, а частота – после него.
24. Классическое определение вероятности. Свойства вероятности события.
Вероятностью события х называется отношение числа исходов, благоприятствующих событию А, к общему числу всех равновозможных попарно несовместных и единственно возможных исходов опыта. Р(А) = 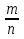
Свойства вероятности события:
Для любого события А 0<=m<=n
Поделив каждый член на n, получим для вероятности любого события А: 0<=Р(А) <=1
Если m=0, то событие невозможно: Р(А)=0
Если m=n, то событие достоверно: Р(А)=1
Если m
25. Геометрическое определение вероятности. Примеры.
Классическое определение вероятности требует рассмотрение конечного числа элементарных исходов, причем равновозможных. Но на практике часто встречаются испытания, число возможных исходов которых бесконечно.
Опр. Если точка случайным образом появляется одномерной\ двумерно\ или 3х мерной области меры S (мера – ее длина, площадь или объём) то вероятность ее появления в части этой области меры S равна
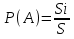 где S – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а Si – мера, выражающая количество благоприятствующих событию A исходов. где S – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а Si – мера, выражающая количество благоприятствующих событию A исходов.
Пример 1. Круг радиусом R помещен меньший круг радиусом г. Найти вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в малый круг.
Пример 2. Пусть отрезок длиной l включается в отрезок длиной L. Най ти вероятность события А «наудачу брошенная точка попала на отрезок длиной l».
|
|
|
 Скачать 7.57 Mb.
Скачать 7.57 Mb.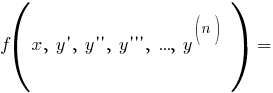
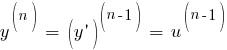
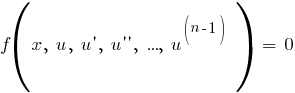
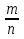
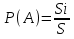 где S – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а Si – мера, выражающая количество благоприятствующих событию A исходов.
где S – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а Si – мера, выражающая количество благоприятствующих событию A исходов.
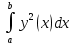



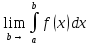 , то это предел – несобственный интеграл от f(x) на
, то это предел – несобственный интеграл от f(x) на 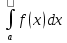
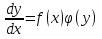 , где
, где 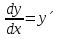
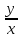 ) называется однородным.
) называется однородным.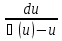 =
= 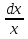 ;
; 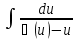 =
= 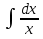 + C
+ C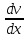 = -v*P(x) ;
= -v*P(x) ; 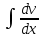 = -
= -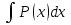 ; ln |v| = -
; ln |v| = - (4)
(4) ; u =
; u = 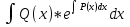 + C (5)
+ C (5)