1. Определение функции нескольких переменных. Основные понятия
 Скачать 7.57 Mb. Скачать 7.57 Mb.
|
|
1. Определение функции нескольких переменных. Основные понятия. Если каждой паре независимых друг от друга чисел (х,у) из некоторого множества по какому-либо правилу ставится в соответствие одно значение переменной z, то она называется функцией двух переменных. z=f(x,y,) Область определения функции z - совокупность пар (х,у), при которых функция z существует. Множество значений (область значений) функции – все значения, которые принимает функция в ее области определения. График функции двух переменных - множество точек P, координаты которых удовлетворяют уравнению z=f(x,y) Окрестность точки M0 (х0;y0) радиуса r – совокупность всех точек (x,y), которые удовлетворяют условию 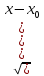 < r < r2. Область определения и область значений функции нескольких переменных. График функции нескольких переменных. (см1) 3. Предел и непрерывность функции нескольких переменных. Число А называется пределом функции f(x,y) при стремлении точки М(х,у) к точке М0(х0,уо), если для любого числа Е>0 найдётся такое число r>0, что для любой точки М(х,у), для которых верно условие ММ0 Записывают: 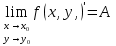 Пусть точка М0(х0,у0) принадлежит области определения функции f(x,y). Тогда функция z=f(x,y) называется непрерывной в точке М0(х0,у0), если 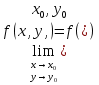 , причём точка М(х,у) стремится к точке М0(х0,у0) произвольным образом. , причём точка М(х,у) стремится к точке М0(х0,у0) произвольным образом.Если в какой-либо точке условие 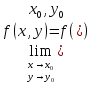 не выполняется, то эта точка разрыва функции f(x,y). Это может быть в случаях: не выполняется, то эта точка разрыва функции f(x,y). Это может быть в случаях:
4. Дифференцируемость функции нескольких переменных, частные производные, полный дифференциал. Функция называется дифференцируемой в данной точке, если ее полное приращение в этой точке может быть представлено в виде: 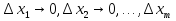 функции, равные 0 при ∆х1=∆х2=…∆хm=0. функции, равные 0 при ∆х1=∆х2=…∆хm=0.Частная производная функции z=f(x,y) по х – предел отношения частного приращения функции по х к приращению Δх при Δх→0, если он существует и конечен: 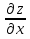 = = 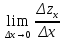 Частная производная функции z=f(x,y) по y- – предел отношения частного приращения функции по y к приращению Δy при Δy→0, если он существует и конечен:: 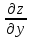 = = 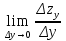 Полный дифференциал функции z=f(x,y) - главная линейная относительно 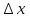 и ∆у часть приращения функции ∆z в точке (х,у). и ∆у часть приращения функции ∆z в точке (х,у).dz= 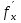 (x,y)dx+ (x,y)dx+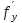 (x,y)dy (x,y)dyЕсли функция f(x,y) определена в некоторой области D, то её частные производные f’x(x,y), f’y(x,y), тоже будут определены в той же области или её части. Будем называть эти производные производными I-ого порядка. Производные этих функций производными II-ого порядка.
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков. 5. Экстремум функции двух переменных: необходимое и достаточное условия. Точка max М0 – это если для функции z=f(x,y), определённой в некоторой области, в некоторой окрестности точки М0(х0,у0), верно неравенство f(x0,y0)≥f(x,y) Точка min М0 – это если для функции z=f(x,y), определённой в некоторой области, в некоторой окрестности точки М0(х0,у0), верно неравенство f(x0,y0)≤f(x,y) Необходимое условие: если функция f(x,y) в точке (х0,у0) имеет экстремум, то в этой точке либо обе её частные производные первого порядка равны 0 f´y(x0,y0)=0, f´x(x0,y0)=0, либо хотя бы одна из них не существует. Эту точку (х0, у0) будут называть критической точкой. Достаточное условие: пусть в окрестности критической точки (х0,у0) функция f(x,y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение: 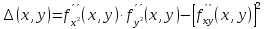
Если 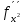 (x0, y0)<0 – max, если (x0, y0)<0 – max, если 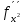 (x0, y0)>0 – min. (x0, y0)>0 – min.
6. Неопределенный интеграл и его свойства. Неопределённый интеграл для функции f(x) - совокупность всех первообразных для функции f(x) на промежутке X Обозначается символом 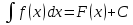 , где С – производная постоянная, f(x) – подынтегральная функция, f(x)dx–подынтегральное выражение, х – переменная интегрирования. , где С – производная постоянная, f(x) – подынтегральная функция, f(x)dx–подынтегральное выражение, х – переменная интегрирования.Свойства: 1) Производная от неопределённого интеграла равна подынтегральной функции, а дифференциал – подынтегральному выражению: 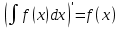 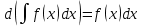 2) Определённый интеграл от производной некой функции равен самой функции + произвольная постоянная C: 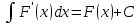 3) Неопределённый интеграл от дифференциала некой функции равен этой функции + произвольная постоянная С: 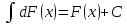 4) Постоянный множитель А (А≠0) можно выносить за знак неопределённого интеграла: 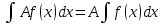 5) Неопределённый интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов этих функций (если каждый из них существует): 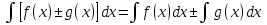 7. Таблица интегралов. 8. Методы интегрирования неопределенного интеграла: непосредственное, подстановки, по частям, разложение дроби на простейшие, тригонометрических функций. 1) Непосредственное интегрирование заключается в преобразовании подынтегральной функции к табличному виду с использованием основных свойств интеграла. 2) Замена переменной (метод подстановки) в неопределённом интеграле состоит в том, что при вынесении интеграла вместо переменной х вводится новая переменная t, связанная с x определённой зависимостью x=γ(t), где γ(t) монотонна и дифференцируема, тогда справедливо равенство 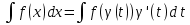 3) Интегрирование по частям: если функции u= γ(u) и u=Ψ(х) непрерывно дифференцируемы на некотором промежутке, то справедлива формула: 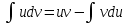 Эта формула называется формулой интегрирования по частям. Применяется для интегрирования произведений и таких функций, как lnx, arcsinx, arccosx, степенной и тригонометрической, степенной и обратной, степенной и логарифмической и других функций. 4) Интегрирование дробей. Элементарными дробями называются дроби следующих 4-ёх типов: 1) 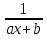 ; 2) ; 2) 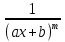 ; 3) ; 3) 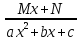 ; 4) ; 4) 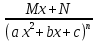 , где m, n – натуральные числа (m≥2, n≥2, b2-4ac<0) , где m, n – натуральные числа (m≥2, n≥2, b2-4ac<0)Дробь 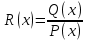 называется правильной, если степень числителя меньше степени знаменателя, в противном случае дробь называется неправильной. называется правильной, если степень числителя меньше степени знаменателя, в противном случае дробь называется неправильной.Если 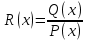 – правильная рациональная дробь, знаменатель P(x) которой представлен в виде линейных и квадратичных множителей P(x)= – правильная рациональная дробь, знаменатель P(x) которой представлен в виде линейных и квадратичных множителей P(x)=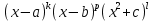 , то эта дробь может быть разложена на элементарные дроби по схеме: , то эта дробь может быть разложена на элементарные дроби по схеме: 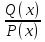 = =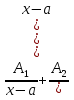 +… +…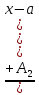 +…+ +…+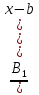 + +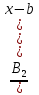 +…+ +…+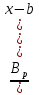 + +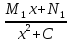 + +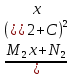 +…+ +…+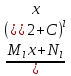 , где A1…Ak, B1 … Bp, M1…Me, N1…Nl – некоторые действительные числа. Коэффициенты Аi, Bi, Mi, Ni находят методом неопределенных коэффициентов или методом частных значений. Для этого необходимо привести равенства к общему знаменателю, приравнять коэффициенты при одинаковых степенях x в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициент и другим способом, придавая в полученном тождестве переменной х произвольное числовое значение. , где A1…Ak, B1 … Bp, M1…Me, N1…Nl – некоторые действительные числа. Коэффициенты Аi, Bi, Mi, Ni находят методом неопределенных коэффициентов или методом частных значений. Для этого необходимо привести равенства к общему знаменателю, приравнять коэффициенты при одинаковых степенях x в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициент и другим способом, придавая в полученном тождестве переменной х произвольное числовое значение. 5) Интегрирование тригонометрических функций: универсальная тригонометрическая подстановка. Интеграла вида 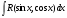 , где R – рациональная функция, приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: tg , где R – рациональная функция, приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: tg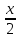 =t =tВ результате подстановки: sinx= 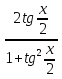 = =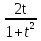 cosx= cosx=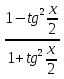 = = 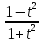 x=2arctg(t) dx= x=2arctg(t) dx=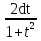 Интегралы вида 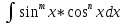 1) Один из показателей m или n – нечетное положительное число. Если n - нечетное положительное число, то подстановка sin x=t Если m - нечетное положительное число, то подстановка cos x=t 2) Оба показателя степени m и n – четные положительные числа. Надо преобразовать подынтегральную функцию с помощью формул: sinx*cosx=½sin(2x) 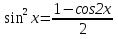 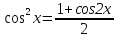 Интегралы вида 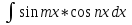 , , 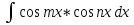 , , 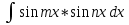 . Подынтегральную функцию преобразовываем с помощью тригонометрических формул: . Подынтегральную функцию преобразовываем с помощью тригонометрических формул:9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ Геометрический смысл определенного интеграла: Криволинейная трапеция – это фигура, ограниченная сверху кривой y=f(x), снизу – отрезком [a;b], слева – прямой х = а, справа – прямой х = b. Определенный интеграл – площадь криволинейной трапеции Достаточное условие существование определенного интеграла: если функция y=f(x) непрерывна на [a;b], то она интегрируема на этом отрезке. Обязательная составляющая криволинейной трапеции – нижнее основание в виде [a;b] и верхняя часть в виде кривой y=f(x). Пусть функция f(x) определена на [a;b]. Разобьем этот промежуток на n произвольных частей точками x0, x1, x2,…xn, полагая, что a=x0 В каждом из полученных частичных промежутков [xi;xi+1], где i=0,1,2…выберем произвольную точку Ęi (xi≤Ęi≥xi+1) 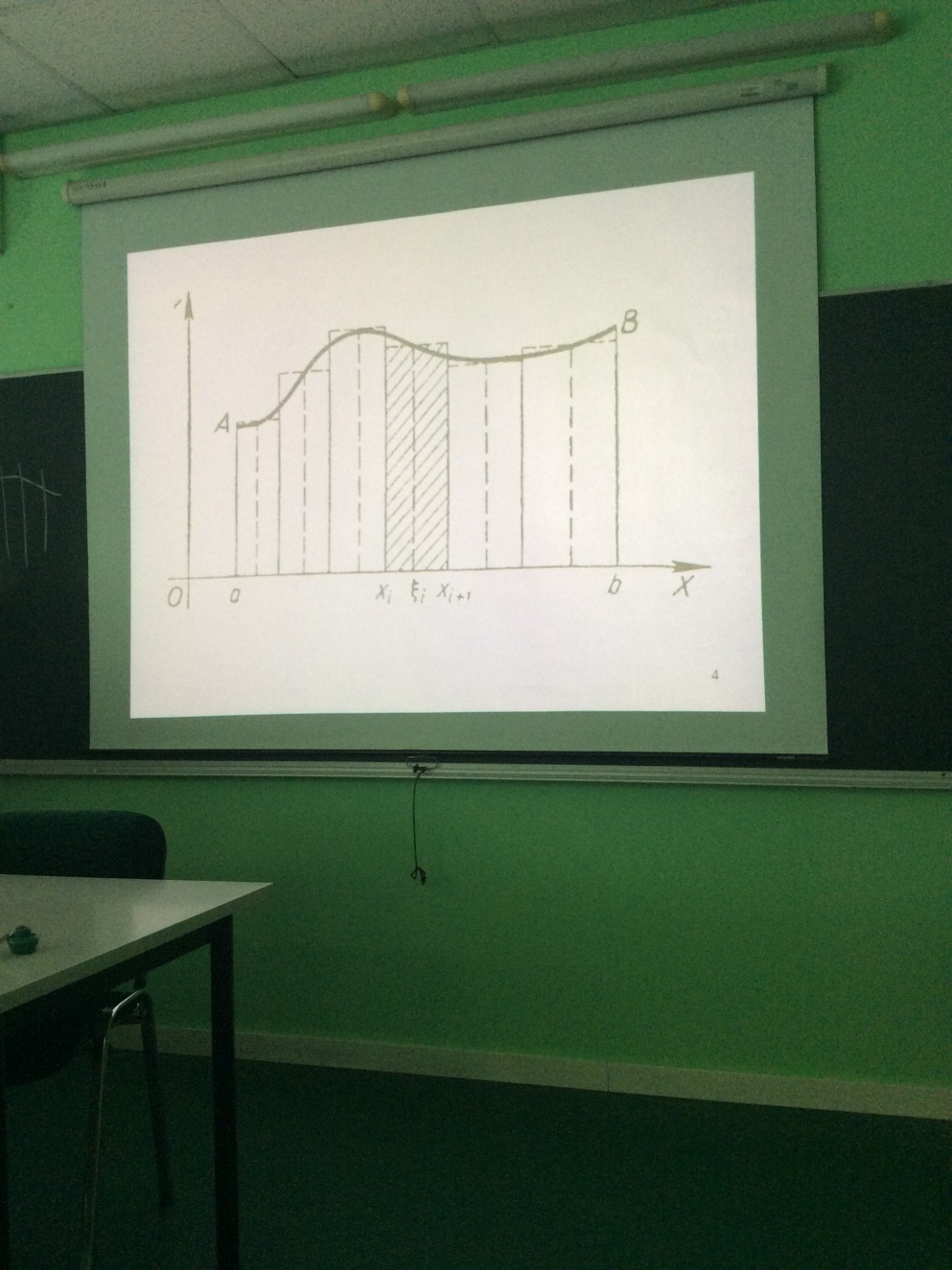 Вычислим значения функций f(Ę) и умножим его на разность xi+1-xi=Δ xi. После этого составим сумму: Если существует конечный предел интегральной суммы при λ→0, не зависящий ни от способа дробления промежутка [a;b] на части, ни от выбора точки Ęi, то этот предел – определенный интеграл функции f(x)по промежутку [a;b]: I= 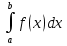  10. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 1) Если переставить пределы интегрирования, то изменится лишь знак: 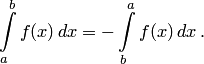 2) Каковы бы ни были а и b, всегда имеет место равенство: 3) Постоянный множитель А выносится за знак определенного интеграла: 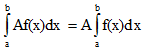 4) Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций: 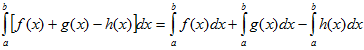 5) Если f(x) – неотрицательная на [a;b], функция и нижний предел меньше верхнего предела (a<b), то и сам интеграл – число неотрицательное, т.е.: Замечание: если f(x) ≤0 на [a;b] и a Если f(x) ≥0 на [a;b] и a>b имеем 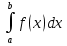 ≤0 ≤0Если f(x) ≤0 на [a;b], то 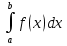 ≥0 ≥06) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то: 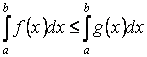 , т.е. неравенство почленно интегрируется. , т.е. неравенство почленно интегрируется.7) Если a ≤ b и f(x) непрерывна на [a, b], то: 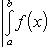 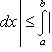 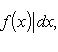 , т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции. , т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то: 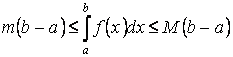 9) Теорема о среднем: Если функция f(x) непрерывна на [a;b], то существует хотя бы одна точка С на этом отрезке, такая, что справедливо равенство: 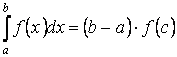 Замечание: формула справедлива также для a>b, кроме a Если a>b, то: 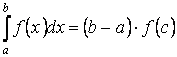 , (b= , (b=Отсюда Геометрический смысл: Если f(x) >=0 на отрезке [a;b], то интеграл левой части есть площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), а правая часть – площадь прямоугольника с тем же основанием и h=f(c). Для площади криволинейной трапеции всегда есть равновеликий ей прямоугольник с тем же основанием и h, равной ординате этой кривой. 10) Определенный интеграл с одинаковыми пределами равен 0. 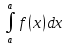 =0 =0Определенный интеграл как функция верхнего предела: В отличие о неопределенного интеграла, определенный интеграл – это число, величина которого зависит только от пределов a и b. Если изменить верхний предел, то величина интеграла изменится. Интеграл с переменным верхним пределом есть функция своего верхнего предела Ф(х): Теорема: производная определенного интеграла от непрерывной функции по его верхнему пределу существует и равна подынтегральной функции в верхнем пределе. 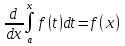 Если функция f(x) – непрерывна, то она имеет первообразную F(x), равную определенному интегралу. 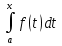 11. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА (основная формула интегрального исчисления (!) ) Если f(x) непрерывна на отрезке [a;b], и F(x) - некоторая первообразная функции f(x), То: 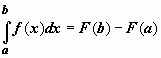 Формулу Ньютона-Лейбница обычно записывают так: 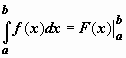 12. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 1) Метод замены переменной. Пусть функция x=φ(t) имеет производную во всех точках отрезка [α;β] и отображает этот отрезок на отрезке [a,b] таким образом, что a= φ(α) и b=φ(β). Тогда 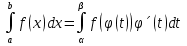 2) Интегрирование по частям Пусть функции u(x) и v(x) имеют производные во всех точках отрезка [a,b]. Тогда: 3) Метод непосредственного интегрирования. С помощью тождественных преобразований подынтегральной функции интеграл сводится к интегралу, к которому применимы основные правила интегрирования и возможно использование таблицы основных интегралов. 4) Интегрирование дробей. Элементарными дробями называются дроби следующих 4-ёх типов: 1) 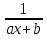 ; 2) ; 2) 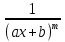 ; 3) ; 3) 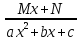 ; 4) ; 4) 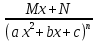 , где m, n–натуральные числа (m≥2, n≥2, b2-4ac<0) , где m, n–натуральные числа (m≥2, n≥2, b2-4ac<0)Дробь 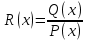 - правильная, если степень числителя меньше степени знаменателя, в противном случае дробь называется неправильной. - правильная, если степень числителя меньше степени знаменателя, в противном случае дробь называется неправильной.Если 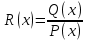 – правильная рациональная дробь, знаменатель P(x) которой представлен в виде линейных и квадратичных множителей P(x)= – правильная рациональная дробь, знаменатель P(x) которой представлен в виде линейных и квадратичных множителей P(x)=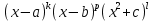 , то эта дробь может быть разложена на элементарные дроби по схеме: , то эта дробь может быть разложена на элементарные дроби по схеме: 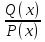 = =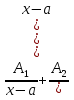 +… +…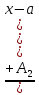 +…+ +…+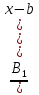 + +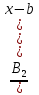 +…+ +…+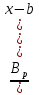 + +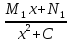 + +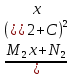 +…+ +…+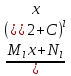 , где A1…Ak, B1 … Bp, M1…Me, N1…Nl – некоторые действительные числа. Коэффициенты Аi, Bi, Mi, Ni находят методом неопределенных коэффициентов или методом частных значений. Для этого необходимо привести равенства к общему знаменателю, приравнять коэффициенты при одинаковых степенях x в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициент и другим способом, придавая в полученном тождестве переменной х произвольное числовое значение. , где A1…Ak, B1 … Bp, M1…Me, N1…Nl – некоторые действительные числа. Коэффициенты Аi, Bi, Mi, Ni находят методом неопределенных коэффициентов или методом частных значений. Для этого необходимо привести равенства к общему знаменателю, приравнять коэффициенты при одинаковых степенях x в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициент и другим способом, придавая в полученном тождестве переменной х произвольное числовое значение. 5)Интегрирование тригонометрических функций: универсальная тригонометрическая подстановка. Интеграла вида 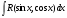 , где R – рациональная функция, приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: tg , где R – рациональная функция, приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: tg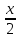 =t =tВ результате подстановки: sinx= 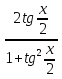 = =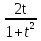 cosx= cosx=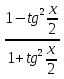 = = 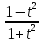 x=2arctg(t) dx= x=2arctg(t) dx=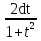 Интегралы вида 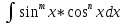 1) Один из показателей m или n – нечетное положительное число. Если n - нечетное положительное число, то подстановка sin x=t Если m - нечетное положительное число, то подстановка cos x=t 2) Оба показателя степени m и n – четные положительные числа. Надо преобразовать подынтегральную функцию с помощью формул: sinx*cosx=½sin(2x) 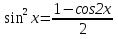 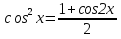 Интегралы вида 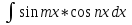 , , 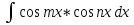 , , 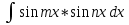 . Подынтегральную функцию преобразовываем с помощью тригонометрических формул: . Подынтегральную функцию преобразовываем с помощью тригонометрических формул:13) ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА а) Пусть f(x) положительна и непрерывна на [a;b]. Тогда площадь криволинейной трапеции, ограниченной сверху кривой y=f(x) выражается определенным интегралом: (выше оси Ox) 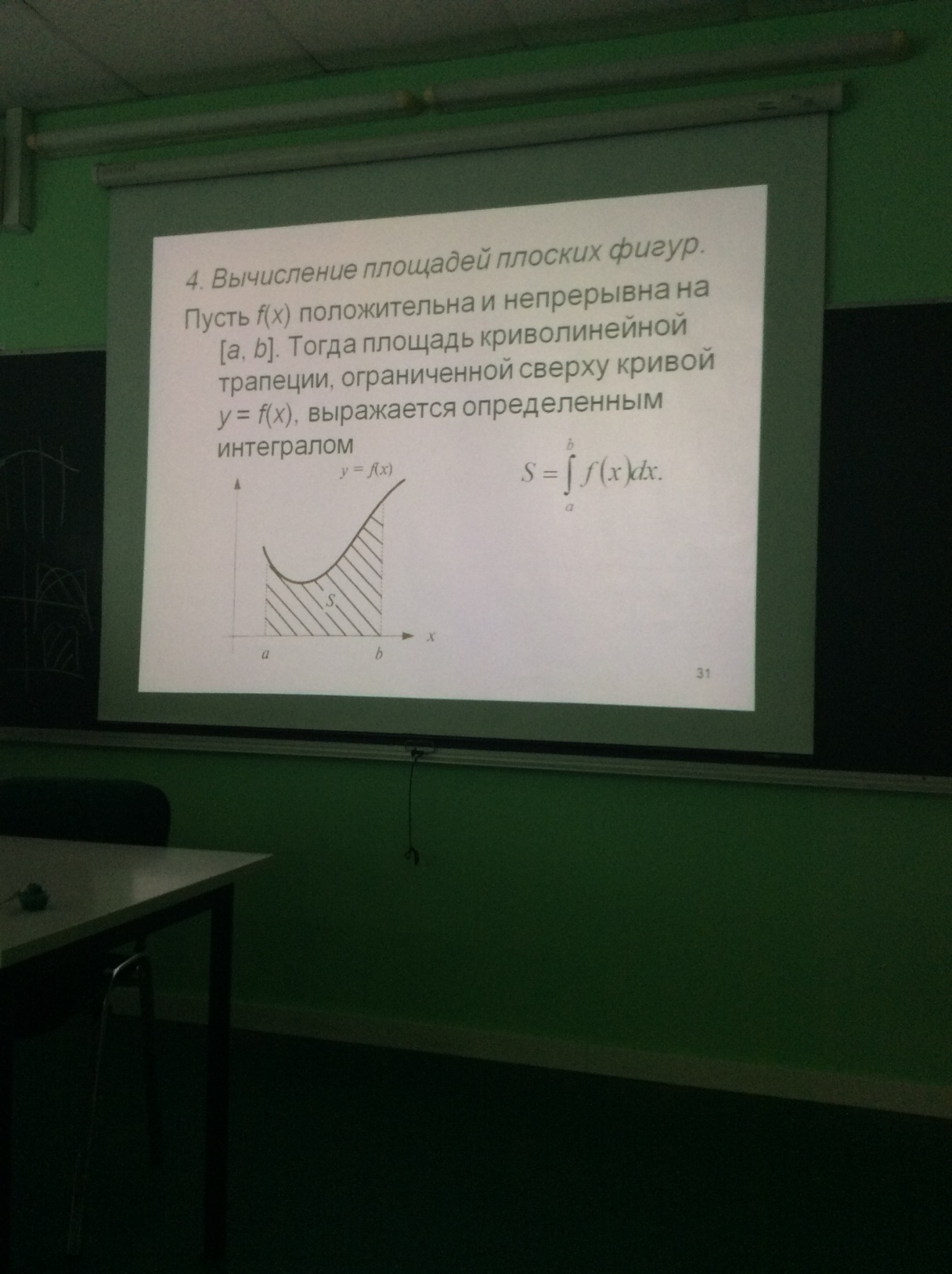 б) Пусть функция y=f(x) отрицательна и непрерывна на [a;b], т.е. кривая y=f(x) и криволинейная трапеция лежат под осью Ох. Тогда:   в) Общий случай, когда некоторые части кривой лежат над осью Ох, а другие – под осью Ох. Площадь криволинейной трапеции - алгебраическая сумма площадей тех частей фигуры, которые расположены над Ох, и тех ее частей, которые под Ох, причем первые входят в сумму с «+», а вторые – с «-». Тогда: 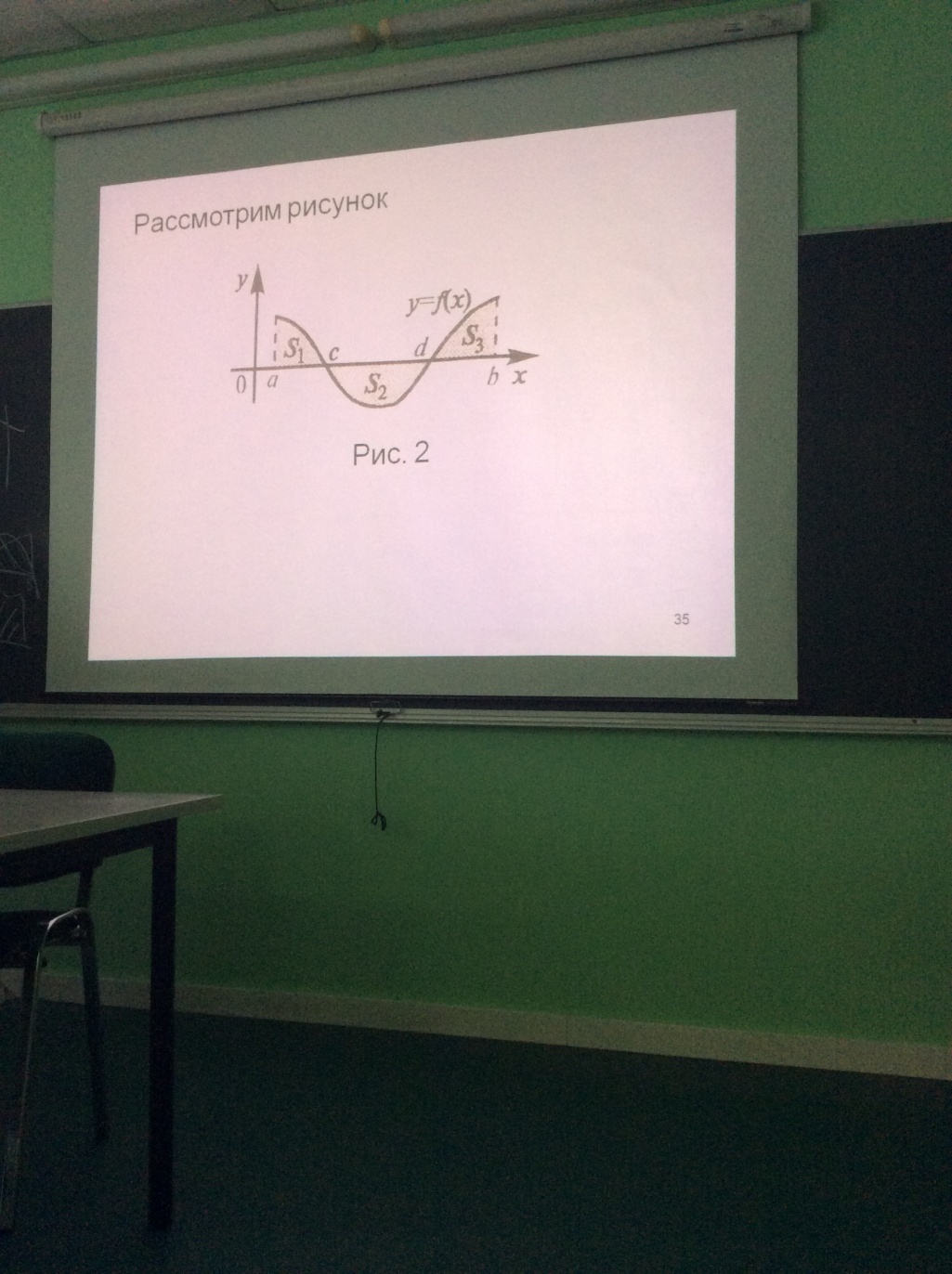 г) Пусть фигура ограничена сверху и снизу кривыми y1=f1(x), y2=f2(x) и f1(x)≤f2(x), a≤x≥b, где f1(x), f2(x) – непрерывные функции. Тогда: |

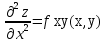 ;
;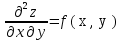 ;
;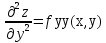 ;
;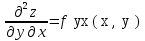 .
.