механика. 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение
 Скачать 0.81 Mb.
|
|
§ В своих трудах «Математические начала натуральной философии», Исаак Ньютон приводит следующую формулировку своего закона [1] Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. § «Школьная формулировка»: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела). Обычно этот закон записывается в виде формулы: , где — ускорение тела, — сила, приложенная к телу, а — масса тела, причём — константа. Или, в более известном виде: § Формулировка второго закона Ньютона, пригодная в случае тел переменной массы: В инерциальной системе отсчета производная импульса материальной точки по времени равна действующей на него силе[2].
 где — импульс (количество движения) тела, — время, а — производная по времени. Уравнения, соответствующие данному закону, называются уравнениями движения материальной точки.
- импульс (количество движения) материальной точки (частицы), m – масса частицы, - скорость частицы. Импульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости: . Масса- физическая величина, являющаяся мерой инерционных (инертная масса) и гравитационных (гравитационная масса ) свойств тела называется инертной массой этого тела. В этом смысле масса выступает как свойство тел не поддаваться изменению скорости как по величине, так и по направлению. Инертная и гравитационная массы равны друг другу. Сила тяжести пропорциональна массе тела, на которое она действует P=mg; (1) Если тело покоится, то вес тела равен силе тяжести, на него действующей, и в формуле (1) можно считать Р весом тела. Значит, для покоящихся тел их веса пропорциональны массам, так что для двух тел с массами m1 и m2 и весами Р1 и Р2 справедливо равенство  Сила- векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры (деформируется). В каждый момент времени сила характеризуется величиной, направлением в пространстве и точкой приложения. Для того чтобы одно тело могло действовать на другое при непосредственном соприкосновении, первое должно быть в особом состоянии. На пример, чтобы действовать на пробку игрушечного пистолета, воздух или пружина должны быть сжаты, и т.д. Любое изменение формы или объема. Сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Единица силы – ньютон. 1 Н = кг 5. 0м/с 52 0. Пусть система состоит из N материальных точек. Силы, действующие на i - ю точку, подразделяются на внутренние, действующие со стороны остальных точек системы, и внешние. В соответствии с 3-м законом Ньютона сумма внутренних сил равна нулю: 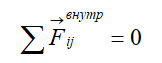 Сумма всех сил, действующих на точки системы, равна сумме внешних сил, действующих на систему. Если система не взаимодействует с внешними телами, то систему называют замкнутой или изолированной. Центром масс (или центром инерции) системы материальных точек называют точку, положение которой определяется радиусом – вектором: 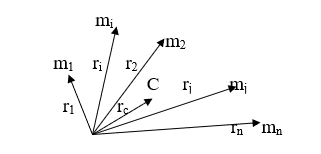 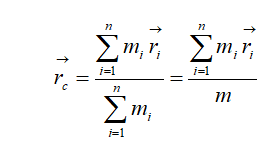 где mᵢ – масса материальной точки, rᵢ - радиус – вектор материальной точки, m – масса всей системы. Центр масс системы совпадает с ее центром тяжести: 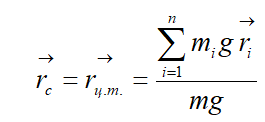 Центр тяжести – точка приложения равнодействующей для сил тяжести всех частей системы. Движение механической системы описывается движением ее центра масс: 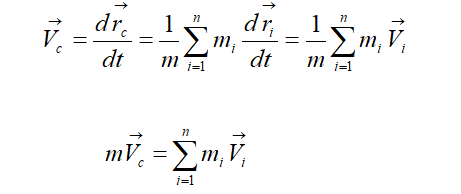 Импульс центра масс системы равен сумме импульсов всех материальных точек системы. Продифференцировав по времени верхнее уравнение (для Vc) получим уравнение движения центра масс: 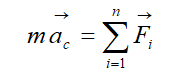 Центр масс движется так, как двигалась бы воображаемая материальная точка с массой, равной массе системы, если к ней приложить результирующую внешнюю силу. 5. Импульс. Закон сохранения импульса. Импульсом силы называют векторную величину, равную произведению силы и времени её действия (F⃗ t). Импульс силы является мерой действия силы за некоторый промежуток времени. Единица импульса силы [F⋅t] = 1 Н · с. 2. С другой стороны, результат действия силы зависит и от характеристик тела, на которое эта сила действует. Зависимость результата действия силы от массы тела можно проиллюстрировать с помощью следующего простого примера. Летящий с некоторой скоростью футбольный мяч, ударяясь о пустую картонную коробку, сдвинет её с места, а, ударяясь о такую же коробку, заполненную металлическими предметами, скорее всего, отскочит от неё, а коробка при этом останется неподвижной. Пуля, летящая со скоростью 2 м/с, при попадании в деревянную стенку в лучшем случае оставит на ней вмятину, а пуля, летящая со скоростью 200 м/с, стенку пробьёт. Таким образом, результат действия силы зависит от массы и скорости взаимодействующих тел. 3. Величину, равную произведению массы тела и его скорости, называют импульсом тела, p⃗ =mv⃗ — импульс тела (или просто импульс). Единица импульса [p] = 1 кг · м/с2. Импульс — величина векторная, поскольку масса — величина скалярная, а скорость — векторная. Импульс — величина относительная, его значение зависит от выбора системы отсчёта, поскольку относительной величиной является скорость. 4. Импульс силы и изменение импульса тела связаны между собой. Запишем второй закон Ньютона: F⃗ =ma⃗ . Подставим в формулу выражение для ускорения a⃗ =v⃗ −v⃗ 0t, F⃗ =m(v⃗ −v⃗ 0)t или F⃗ t=mv⃗ −mv⃗ 0. В левой части равенства стоит импульс силы; в правой части — разность конечного и начального импульсов тела, т.е. изменение импульса тела. F⃗ t=Δ(mv⃗ ). Таким образом, импульс силы равен изменению импульса тела. Это иная формулировка второго закона Ньютона. Именно в таком виде сформулировал свой закон Ньютон. 5. Взаимодействующие между собой тела образуют систему тел. Между телами системы действуют силы взаимодействия: на одно тело — сила F⃗ 1, на другое тело — сила F⃗ 2. При этом сила равна силе и направлена противоположно ей: F⃗ 1=−F⃗ 2 (рис. 41). 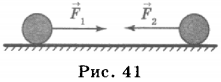 Силы, с которыми тела системы взаимодействуют между собой, называют внутренними силами. Помимо внутренних сил, на тела системы действуют внешние силы. Так взаимодействующие тела притягиваются к Земле. Сила тяготения является в данном случае внешней силой. Если тела движутся, то на них действует сила сопротивления воздуха, сила трения. Они тоже являются внешними силами по отношению к системе, которая в данном случае состоит из двух тел. Ни Земля, ни воздух в эту систему тел не входят. Внешними силами называются силы, которые действуют на тела системы со стороны других тел. Будем рассматривать такую систему тел, на которую не действуют внешние силы. Замкнутой системой тел называют систему тел, взаимодействующих между собой и не взаимодействующих с другими телами. В замкнутой системе действуют только внутренние силы, внешние силы на неё не действуют. 6. Рассмотрим взаимодействие двух тел, составляющих замкнутую систему. Масса первого тела m1, его скорость до взаимодействия v⃗ 01, после взаимодействия v⃗ 1. Масса второго тела m1, его скорость до взаимодействия v⃗ 02, после взаимодействия v⃗ 2. Для этих тел справедливо равенство: m1v⃗ 01+m1v⃗ 02=m1v⃗ 1+m1v⃗ 2 В левой части равенства стоит сумма импульсов тел до взаимодействия, в правой части — сумма импульсов тел после взаимодействия. Как видно, импульс каждого тела при взаимодействии изменился, а сумма импульсов осталась неизменной. Геометрическая сумма импульсов тел, входящих в замкнутую систему, остаётся постоянной при любых взаимодействиях тел этой системы между собой. В этом состоит закон сохранения импульса. 7. Замкнутая система — это идеализация. В реальном мире нет таких систем, на которые не действовали бы внешние силы. Однако в ряде случаев реальные системы взаимодействующих тел можно рассматривать как замкнутые. Это возможно, когда внутренние силы много больше внешних сил, или когда время взаимодействия мало, или когда внешние силы уравновешивают друг друга. Кроме того, в ряде случаев равна нулю проекция внешних сил на какое-либо направление. В этом случае закон сохранения импульса выполняется для проекций импульсов взаимодействующих тел на это направление. 6. Консервативные и неконсервативные силы. Потенциальное силовое поле. Работа и кинетическая энергия. Закон сохранения механической энергии. В механике различают два вида энергии – кинетическую и потенциальную. Кинетическая энергия – функция состояния, определяемая массами движущихся тел и их скоростями. 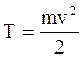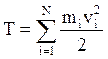Для одной материальной точки  , для системы материальных точек  .Потенциальной называют энергию, обусловленную взаимным расположением тел и силами, действующими между телами. Полная механическая энергия системы равна сумме кинетической и потенциальной энергий: . (1.27) Чтобы ввести понятие потенциальной энергии, рассмотрим сначала, как зависит работа от формы траектории.
Консервативными являются силы тяготения, упругости, электростатические силы и т.д. Поля сил, в которых работа зависит от формы траектории, называются непотенциальными, а силы – неконсервативными. В случае консервативных сил вводится понятие потенциальной энергии.
Естественно считать, что - энергия частицы в начальном положении, - в конечном. Эту энергию называют потенциальной энергией частицы, поднятой над Землей: . (1.29) С учетом (1.29) перепишем (1.28) в следующем виде:  . (1.30)Из этого следует, что работа в потенциальном поле совершается за счет убыли потенциальной энергии частицы. Этот вывод справедлив для любого потенциального поля. Рассмотрим систему материальных точек и обозначим: - результирующая всех внешних сил, действующих на систему; - результирующая всех внутренних консервативных сил; - результирующая всех внутренних неконсервативных сил, действующих на материальные точки. Тогда результирующая всех сил:  . (1.31)Умножим (1.31) скалярно на малое перемещение :  . (1.32)Выясним физический смысл полученной величины:  - работа результирующей силы, которая, как было установлено ранее, равна приращению кинетической энергии системы: ,- работа внешних сил; - работа консервативных сил, равная убыли потенциальной энергии системы: ,  - работа неконсервативных сил.Перепишем (1.31) в виде:  ,или  . (1.33)Принимая во внимание, что , где - полная энергия системы, получим:  .Если система замкнута, то на нее внешние силы не действуют и , тогда:  .Если в системе не действуют неконсервативные силы, например силы трения, то и , т.е.  . (1.34)Выражение (1.34) – математическая запись закона сохранения механической энергии, который гласит: полная энергия замкнутой механической системы, в которой действуют только консервативные силы, не меняется с течением времени. Однако в реальных системах механическая энергия, отдельно взятая, не сохраняется. В любой реальной системе при движении тел возникают силы трения, которые являются неконсервативными силами, тогда  , и полная механическая энергия такой системы убывает. Но при этом механическая энергия переходит в различные виды немеханической энергии, например в энергию теплового движения, т.е. во внутреннюю энергию среды, в которой происходит движение. |
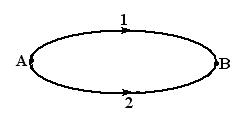Рис.1.12
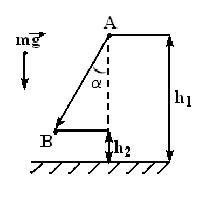Рис.1.13. Движение в поле силы тяжести
. (1.28) Работа характеризует переход тела из одного состояния в другое и в данном случае определяется только начальным h1 и конечным h2положением тела.