механика. 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение

• Название: 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение
• Дата: 11.12.2022
• Размер: 0.81 Mb.
• Имя файла: механика.docx
• Тип: Документы; #839000
• страница: 3 из 6

Поэтому рассмотренный нами закон сохранения и превращения механической энергии является частным случаем всеобщего физического закона сохранения и превращения энергии, который гласит: сумма механической и немеханической энергии замкнутой системы не изменяется, возможны лишь превращения одних видов энергии в другие.
7. Динамика твёрдого тела, момент сил. Основное уравнение динамики вращательного движения.
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точ­ки О в точку А приложения силы, на силу F (рис. 25):

Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении отrк F. Модуль момента силы

 (18.1)

где — угол междуrи F; rsin=l— кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина M_z , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента М_z не зависит от выбора положения точкиОна оси z.

Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

Найдем выражение для работы при вращении тела (рис. 27). Пусть сила F приложе­на в точке В, находящейся от оси z на расстоянии r,— угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dточка приложения В проходит путь ds=rdи работа равна произведе­нию проекции силы на направление смещения на величину смещения: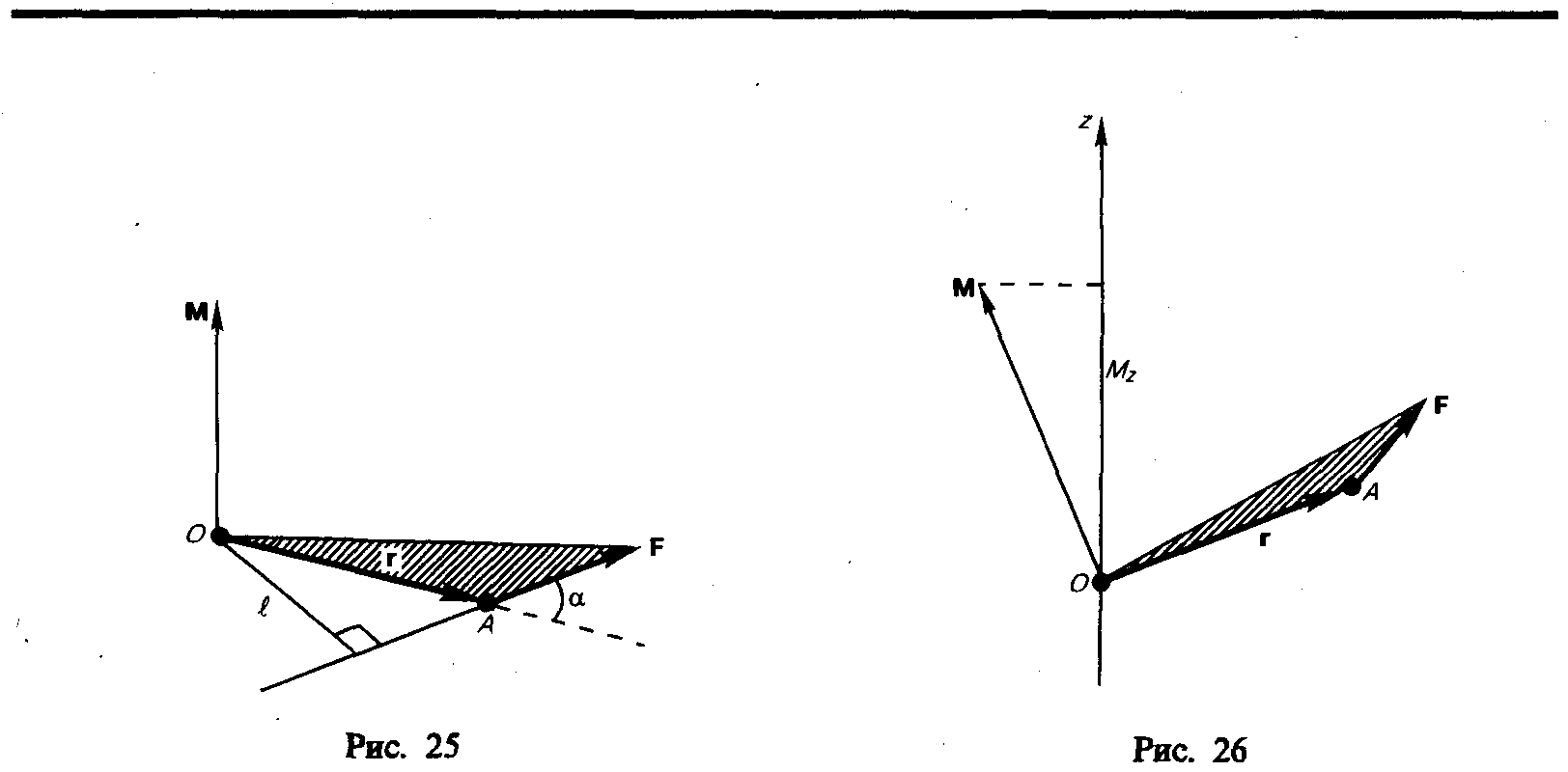

 (18.2)



Учитывая (18.1), можем записать



где Frsin= Fl =M_z —момент силы относительно осиz. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.

Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT,но поэтому M_zd= J_zd,или

Учитывая, что получаем

 (18.3)

Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Можно показать, что если ось zсовпадает с главной осью инерции (см. § 20), проходящей через центр масс, то имеет место векторное равенство

 (18.4)

где J —главный момент инерции тела (момент инерции относительно главной оси).

Момент импульса и закон то сохранения

При сравнении законов вращательного и поступательного движений просматривается аналогия между ними, только во вращательном движении вместо силы «выступает» ее момент, роль массы «играет» момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки Оназывается физическая величина, определяемая векторным произ­ведением:



где r— радиус-вектор, проведенный из точки О в точку A, p=mv —импульс мате­риальной точки (рис. 28); L—псевдовектор,его направление совпадает с направлением поступательного движения правого винта при его вращении отrк р.

Модуль вектора момента импульса



где  —угол между векторами r и р, l— плечо вектораротносительно точки О.

Моментом импульса относительно неподвижной оси zназывается скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульсаL_zне зависит от положения точкиОна оси z.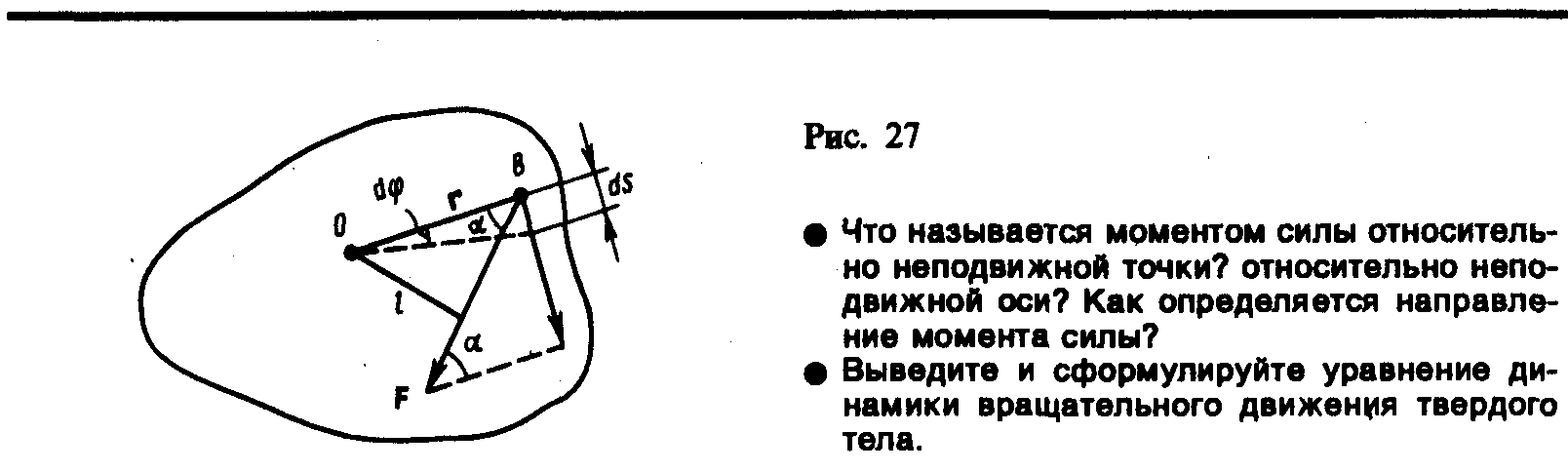



При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдель­ная точка тела движется по окружности постоянного радиуса r_i с некоторой скоро­стью v_i. Скорость v_iи импульс m_iv_i перпендикулярны этому радиусу, т. с. радиус является плечом вектора m_iv_i. Поэтому можем записать, что момент импульса отдель­ной частицы равен

 (19.1)

и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:



Используя формулу (17.1) v_i = r_i, получим



т. е.

 (19.2)

Таким образом, момент импульса твердого тела относительно оси равен произведе­нию момента инерции тела относительно той же оси на угловую скорость. Продифференцируем уравнение (19.2) по времени:



т. е.



Это выражение — еще одна форма уравнения динамики вращательного движения твер­дого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.



Можно показать, что имеет место векторное равенство

 (19.3)

В замкнутой системе момент внешних сил  откуда

 (19.4)

Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью. е. с инвариантностью физических законов относительно выбора направления осей координат системы от­счета (относительно поворота замкнутой системы в пространстве на любой угол).

Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидящий на скамье, которая без трения вращается вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 29), приведен во вращение с угловой скоростью ₁. Если человек прижмет гантели к себе, то момент инерции системы уменьшится. Поскольку момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения₂возрастает. Аналогич­но, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.

8. Моменты инерции (материальная точка, диск, обруч, шар, стержень). Теорема Гюйгенса – Штейнера.

Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Д 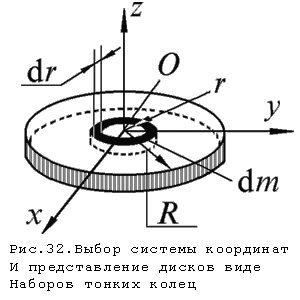ля расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним

радиусом r и наружным r+dr. Площадь такого кольца ds=2r $\pi$ dr, а его масса  , гдеS= $\pi$ R² - площадь всего диска. Момент инерции тонкого кольца найдется по формуле dJ=dmr². Момент инерции всего диска определяется интегралом

Вычисление момента инерции тонкого стержня:

Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых  . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции , т.е.      Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим 

Момент инеpции обручаотносительно оси, пpоходящей чеpез центp кольца пеpпендикуляpно к его плоскости. В этом случае все элементаpные массы обруча удалены от оси на одинаковое pасстояние, поэтому в сумме (3.18) r2 можно вынести за знак суммы, т. е.     

Теорема Штейнера:

В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями: J=J0+ma^2.

Например, момент инерции диска относительно оси О' в соответствии с теоремой Штейнера: 

Момент инерции однородного тела вращения. Моменты инерции конуса, шара.

Линия  - ось вращения.

- масса на квадрат радиуса окружности, по которой движется материальная точка.

Все тело мысленно разбиваем на маленькие объемы. Масса этого кусочка  .



Твердое тело представляется как совокупность системы точечных масс.

- расстояние, на котором находится точка от оси вращения.



- общий алгоритм определения собственного момента инерции твердого тела, относительно оси проходящей через центр инерции данного тела.

Момент инерции шара.

     Сплошной шар массы m и радиуса R можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm , радиусом r, толщиной dr (рис.35).

      Рассмотрим малый элемент сферического слоя $\delta$ m с координатами x, y, z. Его моменты инерции относительно осей проходящих через центр слоя - $\delta$ J_x, $\delta$ J_y, $\delta$ J_z, равны   Т. е. можно записать      (п.26)

     Так как для элементов сферического слоя x²+y²+z²=r² то        После интегрирования по всему объему слоя получим      (п.27)

     Так как, в силу симметрии для сферического слоя dJ_x=dJ_y=dJ_z=dJ , а  , то Интегрируя по всему объему шара, получаем       Окончательно (после интегрирования) получим, что момент инерции шара относительно оси, проходящей через его центр равен 

Разобьём КОНУС на цилиндрические слои   ось толщиной dr. Масса такого слоя   dm = r²dr,

где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя dI = dm^.r².

Момент инерции всего конуса   складывается из моментов инерции всех слоёв:

 I =  =  ρπ r⁴ dr =  ρR⁵.

Остаётся выразить его через массу всего цилиндра: m =  =  =R³,

отсюда    ρ =  , I =   =  mR².

9. Момент импульса твёрдого тела. Закон сохранения момента импульса. Кинетическая энергия вращения.

Моментом импульса материальной точки, вращающейся относительно неподвижной оси OO′, называется величина L, равная произведению импульса  этой точки на расстояниеr от этой точки до оси вращения:  .

Момент импульса является векторной величиной. Вектор  направлен по оси вращения в соответствии с правилом правого винта.

При вращении твердого тела относительно неподвижной оси отдельные его точки, находящиеся на различном расстоянии  от оси вращения, имеют различные скорости . Поэтому для того, чтобы найти момент импульса твердого тела относительно некоторой оси вращения, необходимо разбить это тело на элементарные объемы так, чтобы каждый элементарный объем можно было рассматривать как материальную точку массой  , находящуюся на расстоянии от оси вращения и движущаяся со скоростью .

Тогда момент импульса твердого тела L равен суммемоментов импульсавсех n материальных точек массами  , на которые разбито это тело:

.

Так как для твердого тела угловая скорость вращения  всех материальных точек, на которые разбито это тело, одинакова, то, используя формулу , получим



или в векторной форме:  .

Таким образом, момент импульса твердого тела относительно оси вращения равен произведению момента инерции этого тела относительно той же оси вращения на угловую скорость вращения этого тела.

Продифференцировав это уравнение по времени, получим:

, откуда  .

То есть

.

Это выражение – еще одна форма (называемая дифференциальной) уравнения динамики вращательного движения твердого тела: скорость изменения момента импульса твердого тела относительно оси вращения равна векторной сумме моментов всех действующих на это тело сил относительно той же оси вращения.

В замкнутой системе векторная сумма моментов внешних сил равна нулю. Тогда  и, следовательно, .

Таким образом, момент импульса замкнутой системы сохраняется, что является законом сохранения момента импульса.