механика. 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение

• Название: 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение
• Дата: 11.12.2022
• Размер: 0.81 Mb.
• Имя файла: механика.docx
• Тип: Документы; #839000
• страница: 6 из 6

15. Цикл Карно и теоремы Карно.

Сочетая различные термодинамические процессы, можно получить множество циклов, каждому из которых будет соответствовать определённое значение термического КПД η_t. Возникает естественный вопрос, какой же цикл будет иметь η_t = η_t max.

При исследовании проблемы повышения КПД тепловых машин, Сади Карно в 1824 году был предложен идеальный обратимый цикл, носящий в настоящее время его имя.

Н 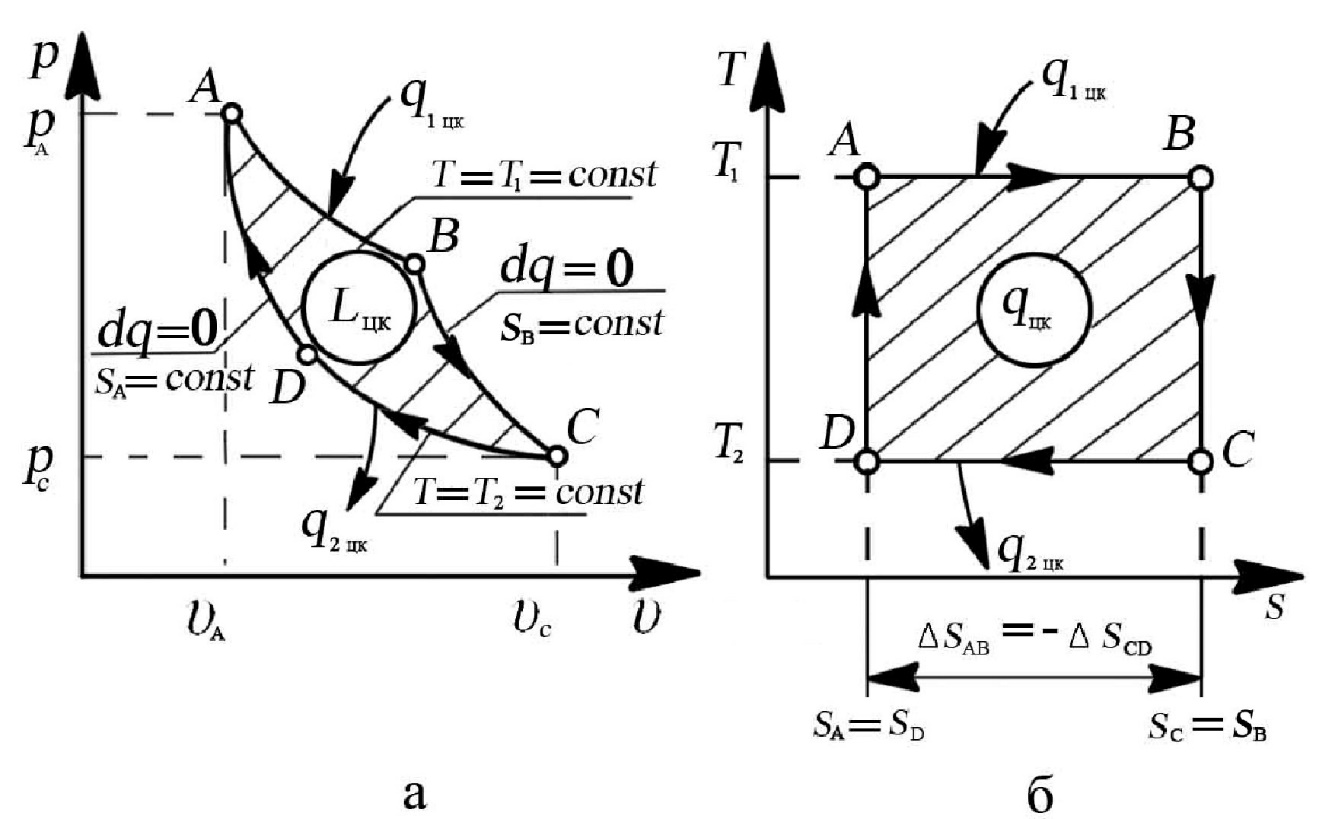 а рис. 4.3. показан идеальный обратимый цикл Карно в рабочей и тепловой диаграммах.

Рис. 4.3. Цикл Карно: а – изображение цикла Карно в рабочей “p-υ” диаграмме,

б – изображение цикла Карно в тепловой “T-s” диаграмме

Процессы, составляющие этот цикл, протекают следующим образом. Пусть теплоотдатчик имеет постоянную температуру T₁, а теплоприемник – постоянную температуру T₂ < T₁.

Считаем, что их размеры настолько велики, что подвод теплоты q_{1 цк} к рабочему телу и отвод от него теплоты q_{2 цк} на величину T₁ и T₂ не влияют. Рабочим телом является идеальный газ.

От исходного состояния А (рис. 4.3,а) рабочее тело расширяется изотермически (T₁ = const) до состояния В, получая от теплоотдатчика теплоту q_{1 цк}. Дальнейшее расширение происходит адиабатным процессом ВС до тех пор, пока температура рабочего тела не снизится до величины T₂. Для возвращения рабочего тела в исходное состояние осуществляется его сжатие в изотермическом процессе CD (T₂ = const). При этом в теплоприемник отводится теплота q_{2 цк}. Цикл замыкается адиабатным процессом сжатия DA,в котором рабочее тело возвращается в исходное состояние A с температурой T₁. Таким образом, цикл Карно состоит из двух изотермических и двух адиабатных процессов.

Заметим, что поскольку цикл обратим, то изотермические процессы подвода и отвода тепла должны происходить при бесконечно малой разнице между температурами теплоотдатчика (или теплоприемника) и рабочего тела. Это позволяет считать, что в процессе изотермического расширения температура рабочего тела равна температуре теплоотдатчика T₁, а в процессе изотермического сжатия – температуре теплоприемника T₂.

На рис. 4.3,б цикл Карно представлен в тепловой “T-s” диаграмме:

1. В “T-s” диаграмме изотермический процесс подвода тепла к системе изображается линией AB, параллельной оси абсцисс. В этом процессе рабочее тело получает теплоту q_{1 цк} > 0, в результате чего его энтропия возрастает от s_Aдо s_B на величину:

 . (4.5)

2. Далее следует адиабатное расширение по линии BC, в ходе которого температура рабочего тела уменьшится от T₁ до T₂, и при этом энтропия рабочего тела остаётся неизменной s_B = s_С.

3. При температуре T₂ происходит изотермический процесс сжатия по линии CD, в ходе которого рабочее тело отдает приёмнику теплоту в таком количестве q_{2 цк}, чтобы энтропия рабочего тела от значения s_B = s_С, снова вернулась к значению s_A = s_D,

 ^. (4.6)

4. Цикл завершается адиабатным сжатием DA, в ходе которого температура повышается от T₂ до T₁, принимая, таким образом, первоначальное значение.

Теперь легко определить КПД цикла Карно, т.е. КПД идеального теплового двигателя. В уравнение (4.4) подставим значения количеств теплоты q_{1 цк} и q_{2 цк} из (4.5 и 4.6), выраженных через температуры и изменения энтропии в процессах AB и CD:

 .

Так как Δs_AB = |Δs_CD|, имеем, что:

 . (4.7)

Из полученного выражения (4.7) видно, что термический КПД цикла Карно зависит только от температур источника (T₁) и приёмника (T₂) теплоты. Никакие физические свойства рабочего тела не вошли в выражение для η_t цк. Эти выводы составляют содержание так называемой теоремы Карно, которая формулируется следующим образом: Термический КПД цикла Карно зависит только от температур теплоотдатчика (T₁) и теплоприёмника (T₂) и не зависит от свойств рабочего тела.

Из анализа формулы (4.7) следует:

1. Чем выше T₁ и чем ниже T₂, тем выше η_t цк.

Хотя в настоящее время имеется техническая возможность получения очень высоких температур (сотни тысяч градусов), однако в реальных двигателях использовать эти температуры практически не представляются возможным, так как материалы, из которых изготовлены детали двигателей, не способны выдерживать такие температуры. Максимальная температура (T₁), практически реализуется в большинстве двигателей, близка к 1000…2000 К. Имеются двигатели (например, ракетные), в которых используются более высокие температуры до 4000 К. Однако эти двигатели рассчитаны на очень короткий срок службы (не более нескольких десятков минут).

Что касается температуры T₂, то она приблизительно составляет 300 К, поскольку приёмником теплоты для всех двигателей, работающих в наземных условиях, является либо атмосферный воздух, либо вода в водоемах, реках, морях.

Вообще говоря, искусственно может быть получена температура, даже близкая к нулю, однако получение температур ниже температуры окружающей среды связанно с затратой работы. Затрата работы оказывается больше, чем выигрыш в КПД, поэтому такой путь увеличения КПД оказывается неприемлемым.

2. Эффективность превращения теплоты в работу (термический КПД) в любом цикле не может быть больше, чем в цикле Карно, осуществляемом в том же интервале температур.

3. Термический КПД цикла Карно всегда меньше единицы, так как не существует источников теплоты с бесконечно высокой температурой (T₁ =   ) или же приемников теплоты (T₂ = 0), то соотношение T₂/T₁ всегда больше нуля. Следовательно, КПД цикла Карно, а тем более любого другого цикла всегда меньше единицы.

4. Когда T₁ = T₂, термический КПД цикла η_t цк = 0, следовательно, если все тела термодинамической системы имеют одинаковую температуру, т.е. находится в тепловом равновесии, то преобразование теплоты в работу невозможно.

Хотя теоретически цикл Карно является наиболее экономичным циклом, он не нашел практической реализации в тепловых машинах, использующих в качестве рабочего тела различные газы.

Цикл Карно с газообразным рабочим телом осуществлять нельзя, т.к. обеспечить изотермическое сжатие с непрерывным отводом теплоты в изотермическом компрессоре и изотермическое расширение с непрерывном подводом теплоты в изотермической турбине. Только в паросиловых установках отвод теплоты и иногда частично подвод теплоты происходят при постоянных температурах в процессах конденсации пара и при парообразовании.

В тепловом двигателе, работающему по циклу Карно и развивающему необходимую для практических целей мощность, диапазон изменения давления и объёма рабочего тела должен быть настолько большим, что двигатель получился бы недопустимо громоздким и тяжелым.

Смысл рассмотрения цикла Карно заключается в том, что его энергетические показатели L_цк и η_t цк являются предельно высокими по сравнению с любимыми другими циклами тепловых машин в заданном интервале температур максимальной T₁ = T_г и минимальной T₂ = T_н.

Поэтому показатели цикла Карно являются общим критерием оценки энергетической эффективности тепловых установок, в том числе ГТД и ДВС.

Таким образом, цикл Карно является базовым для оценки совершенства любого произвольного цикла, в том числе и цикла авиационного ГТД.

16. Второе начало термодинамики. Обратимые и необратимые процессы. Энтропия.

Второй закон термодинамики (второе начало термодинамики): самопроизвольно протекают процессы, приводящие к увеличению общей энтропии системы и окружающей среды

ΔS_сист + ΔS_среды ≥ 0 или ΔS ≥ 0

Для химической реакции изменение энтропии   прод -   исх

Энтропия (S) -мера энергетического беспорядка в системе, мера хаоса, мера той энергии, которая рассеивается в виде тепла и не превращается в работу.

Изменение энтропии ∆S наиболее просто определяется для обратимых изотермических процессов, оно равняется тепловому эффекту процесса, делённому на абсолютную температуру. Энтропия – экстенсивная функция. Энтропия системы равна сумме энтропий составных частей. Её изменение зависит только от начального и конечного состояния системы и не зависит от пути перехода.

Энтропию относят к 1 молю вещества в стандартных условиях S°298 ; измеряют ее в энтропийных единицах (э.е.): 1 Дж/мoль*К = 1 э.е.

Больцман постулировал, что энтропия связана с термодинамической вероятностью логарифмической зависимостью

 S = k ln W уравнение Больцмана

k – константа Больцмана: k = 1,38∙10^-23 Дж/градус;

W – число микросостояний, с помощью которых можно реализовать данное макросостояние: W=   ;

Р – вероятность того, что система находится именно в этом микросостоянии.

Термодинамически обратимый процесс– процесс, протекающий в прямом и в обратном направлении без изменений в системе и в окружающей среде, т.е. при переходе из начального состояния в конечное все промежуточные состояния являются равновесными.

При наличии неравновесных промежуточных состояний процесс считают термодинамически необратимым.

Энергия Гиббса. Прогнозирование направления самопроизвольно протекающих процессов в изолированной и закрытой системах; роль энтальпийного и энтропийного факторов. Термодинамические условия равновесия.

Энергия Гиббса– функция состояния, являющаяся критерием самопроизвольности процессов в открытых и закрытых системах.

G=H–TS

H- энтальпия,

Т- температура,

S- энтропия.

Изменение ЭГ определяется формулой: ΔG=ΔH–TΔS Стандартная ЭГ определяется формулой:



где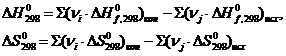



Критериями направления самопроизвольного протекания необратимых процессов являются неравенства ΔG<0 (для закрытых систем),ΔS> 0 (для изолированных систем). Самопроизвольное течение реакций в закрытых системах контролируется как энтальпийным (ΔrH), так и энтропийным (ΔrS) фактором. Для реакций, у которых ΔrH<0 и ΔrS> 0, энергия Гиббса всегда будет убывать, т.е. ΔrG< 0, и такие реакции могут протекать самопроизвольно при любых температурах

В изолированных системах энтропия максимально возможное для данной системы значение S_max; в состоянии равновесия ΔS= 0.