механика. 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Изотермический процесс (T = const) Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:
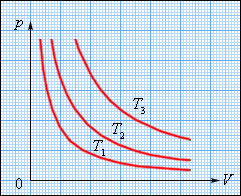
На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p 1 / V, которые называются изотермами. Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис..1). Уравнение изотермического процесса было получено из эксперимента английским физиком Р. Бойлем (1662 г.) и независимо французским физиком Э. Мариоттом (1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.
Изохорный процесс (V = const) Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным. Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p T или
На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 2).
Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля. Уравнение изохорного процесса может быть записано в виде:
где p0 – давление газа при T = T0 = 273,15 К (то есть при температуре 0 °С). Коэффициент α, равный 1/273,15 К–1, называют температурным коэффициентом давления. Изобарный процесс (p = const) Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p. Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:
где V0 – объем газа при температуре 0 °С. Коэффициент α равен 1/273,15 К–1. Его называют температурным коэффициентом объемного расширения газов. На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3), которые называются изобарами.
Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Ж. Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака. Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа. 13. Первое начало термодинамики. Теплота. Теплоёмкость. Первое начало термодинамики: количество теплоты Q, сообщенное системе, идет на увеличение внутренней энергии системы U и на совершение системой внешней работы А:
Например, если газу под поршнем сообщить некоторое количество теплоты, он нагреется (увеличится внутренняя энергия газа) и переместит поршень (газ совершит работу). Внутренняя энергия есть функция температуры. Чем выше температура тела, тем быстрее движутся его молекулы, а, значит, больше внутренняя энергия тела. Если система получает тепло, Q > 0, если отдает, Q < 0; если работает система, A > 0, если работа над системой, A < 0. Первое начало термодинамики, по существу, является законом сохранения энергии: полная энергия, переданная системе Q, превращается в тепловую энергию молекул системы U и в механическую энергию А. Он справедлив не только для газов, но и для жидкостей, и для твердых тел. Если процесс медленный (равновесный), этот закон можно записать в ви-
Пусть газ, находящийся под давлением Р медленно сдвинул поршень площади S на бесконечно малое расстояние dx. Тогда совершенная газом элементарная (бесконечно малая) работа δA = Fdx = PSdx = PdV. Полная работа газа при изменении объема от V1 до V2 получается интегрированием (суммированием бесконечно малых работ):
V1 Для характеристики процессов теплообмена введем понятия молярная и удельная теплоемкость вещества (не обязательно газа). Внутренняя энергия – это функция состояния системы, для идеального газа зависящая только от температуры. Для равновесных процессов функция U(T) дифференцируемая и для нее определен дифференциал dU = U′(T)dT, где U′(T) – производная функции U(T) по температуре. Напротив, количество теплоты и работа не являются функциями состояния системы: нельзя сказать, что у системы такая-то теплота или такая-то работа. Для них дифференциал не определен. Поэтому бесконечно малые приращения этих величин обозначены по-другому. Молярная теплоемкость – это отношение бесконечно малого количества теплоты, полученного молем вещества, к соответствующему приращению его температуры:
Удельная теплоемкость – это отношение бесконечно малого количества теплоты, полученного килограммом вещества, к соответствующему прираще-
Эти теплоемкости связаны между собой простым соотношением С = μс и измеряются соответственно в Дж/(моль·К) и в Дж/(кг·К). Чем больше теплоемкость, тем медленнее вещество нагревается и медленнее остывает. Например, в холодную погоду водоемы охлаждаются медленнее окружающего воздуха и вблизи них теплее (в холодную погоду водоплавающие птицы сидят на воде). А в жару, наоборот, вода нагревается медленнее окружающего воздуха, и вблизи водоемов прохладнее. Это обусловлено тем, что теплоемкость воды гораздо больше теплоемкости воздуха. Для газов, как правило, пользуются молярной теплоемкостью, а для жидкостей и твердых тел – удельной1. Например, из формулы (8.4) легко получить школьную формулу для количества тепла, которое нужно сообщить телу массы m, чтобы нагреть его от температуры t1 до температуры t2 δQ = mcdT. Считая, что масса в процессе не меняется, а теплоемкость не зависит от температуры, получим T2 Q = ∫δQ = mc∫dT = mc(T2 −T1) = mc T . T1 Так как разница температур в кельвинах и градусах Цельсия одинакова, то
Аналогично из формулы (8.3) можно получить похожее выражение для теплоты через молярную теплоемкость и количество вещества. В термодинамике особо рассматриваются следующие молярные теплоемкости: молярная теплоемкость при постоянном объеме
и молярная теплоемкость при постоянном давлении.
Для идеального газа эти теплоемкости связаны между собой уравнением СР = CV + R. (8.6) Для идеального газа в диапазоне средних температур (100-1000 К) теплоемкость CV рассчитывается из молекулярно-кинетических принципов, см. приложение к главе II. Не вдаваясь в детали расчета, отметим, что для одноатомно- го газа CV = 32 R , для двухатомного CV = 52 R , для трех- и более CV = 3R. Для термодинамических расчетов воздух обычно считают двухатомным газом. 14. Адиабатный процесс, уравнение Пуассона. Адиабатический, процесс — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена ( где Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит: Здесь Адиабата Пуассона Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением где 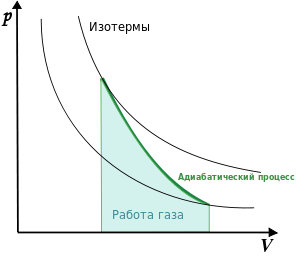 График адиабаты (жирная линия) на диаграмме для газа. С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду где Поскольку При адиабатическом процессе показатель адиабаты равен Для нерелятивистского невырожденного одноатомного идеального газа Для реальных газов показатель адиабаты отличается от показателя адиабаты для идеальных газов, особенно для низких температур, когда большую роль начинает играть межмолекулярное взаимодействие. Один из методов для экспериментального определения показателя был предложен в 1819 г. Клеманом и Дезормом. Стеклянный баллон вместимостью несколько литров наполняется исследуемым газом при давлении | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 1
1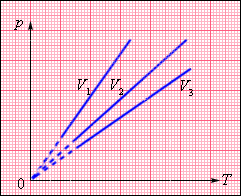 2
2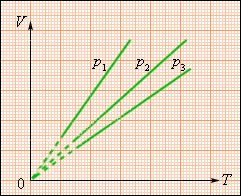 3
3