механика. 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
10. Гармонические колебания. Физический маятник. Физический маятник – это твердое тело, имеющее ось вращения и совершающее колебания под действием тангенциальной составляющей силы тяжести F(F= mgsin(рис. 7), где – отклонение физического маятника от положения равновесия). Р 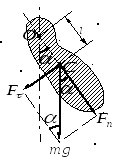 ис. 7 ис. 7Если физический маятник массой m отклонен от положения равновесия на некоторый угол , то момент M возвращающей силы F : где l – плечо силы F, то естьрасстояние от центра масс (точка С) до оси маятника (рис. 7). В случае малых колебаний физического маятника,то есть для малых углов отклонения маятника от положения равновесия sin и тогда По второму закону Ньютона для вращательного движения твердого тела: где I — момент инерции маятника относительно его оси. Знак минус в последнем уравнении обусловлен тем, что вектора момента возвращающей силы и угла поворота имеют противоположные направления. Обозначив Решением этого дифференциального уравнения является функция где 0 – круговая (циклическая) частота; (0t+0) – фаза колебаний в момент времени t; 0 – начальная фаза колебаний. Период малых гармонических колебаний физического маятника: 11. Плоская волна в однородной среде. Сферическая волна. Рассмотрим некоторую упругую среду - твёрдую, жидкую или газообразную. Если в каком-либо месте этой среды возбудить колебания её частиц, то вследствие взаимодействия между частицами, колебания будут, передаваясь от одной частицы среды к другой распространяться в среде с некоторой скоростью . Процесс распространения колебаний в пространстве называется волной.  Если частицы в среде колеблются в направлении распространения волны, то она называется продольной. Если колебания частиц происходят в плоскости, перпендикулярной направлению распространения волны, то волна называется поперечной. Поперечные механические волны могут возникнуть только в среде, обладающей ненулевым модулем сдвига. Поэтому в жидкой и газообразной средах могут распространяться только продольные волны. Различие между продольными и поперечными волнами наиболее хорошо видно на примере распространения колебаний в пружине - см. рисунок. Если частицы в среде колеблются в направлении распространения волны, то она называется продольной. Если колебания частиц происходят в плоскости, перпендикулярной направлению распространения волны, то волна называется поперечной. Поперечные механические волны могут возникнуть только в среде, обладающей ненулевым модулем сдвига. Поэтому в жидкой и газообразной средах могут распространяться только продольные волны. Различие между продольными и поперечными волнами наиболее хорошо видно на примере распространения колебаний в пружине - см. рисунок.Для характеристики поперечных колебаний необходимо задать положение в пространстве плоскости, проходящей через направление колебаний и направление распространения волны - плоскости поляризации. Область пространства, в которой колеблются все частицы среды, называется волновым полем. Граница между волновым полем и остальным пространством среды называется фронтом волны. Иначе говоря, фронт волны - геометрическое место точек, до которых колебания дошли к данному моменту времени. В однородной и изотропной среде направление распространения волны перпендикулярно к фронту волны. Пока в среде существует волна, частицы среды совершают колебания около своих положений равновесия. Пусть эти колебания являются гармоническими, и период этих колебаний равен Т . Частицы, отстоящие друг от друга на расстояние (22.1) вдоль направления распространения волны, совершают колебания одинаковым образом, т.е. в каждый данный момент времени их смещения одинаковы. Расстояние называется длиной волны. Другими словами, длина волны есть расстояние, на которое распространяется волна за один период колебаний. Геометрическое место точек, совершающих колебания в одной фазе называется волновой поверхностью. Фронт волны – частный случай волновой поверхности. Длина волны – минимальное расстояние между двумя волновыми поверхностями, в которых точки колеблются одинаковым образом, или можно сказать, что фазы их колебаний отличаются на . Если волновые поверхности являются плоскостями, то волна называется плоской, а если сферами – то сферической. Плоская волна возбуждается в сплошной однородной и изотропной среде при колебаниях бесконечной плоскости. Возбуждение сферической можно представить в виде результата радиальных пульсаций сферической поверхности, а также как результат действия точечного источника, размерами которого по сравнению с расстоянием до точки наблюдения можно пренебречь. Поскольку любой реальный источник имеет конечные размеры, на достаточно большом расстоянии от него волна будет близка к сферической. В то же время участок волновой поверхности сферической волны по мере уменьшения его размеров становится сколь угодно близким к участку волновой поверхности плоской волны. Уравнение плоской волны, распространяющейся В произвольном направлении 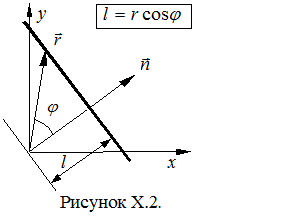 Получим. Пусть колебания в плоскости, параллельной волновым поверхностям и проходящей через начало координат, имеют вид: Получим. Пусть колебания в плоскости, параллельной волновым поверхностям и проходящей через начало координат, имеют вид:В плоскости, отстоящей от начала координат на расстояние l , колебания будут отставать по времени на . Поэтому уравнение колебаний в этой плоскости имеет вид: Из аналитической геометрии известно, что расстояние от начала координат до некоторой плоскости равно скалярному произведению радиус-вектора некоторой точки плоскости на единичный вектор нормали к плоскости: . Рисунок иллюстрирует данное положение для двумерного случая. Подставим значение l в уравнение (22.13): 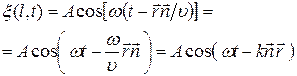 (22.14) (22.14)Вектор , равный по модулю волновому числу и направленный по нормали к волновой поверхности, называется волновым вектором. Уравнение плоской волны можно теперь записать в виде: Функция (22.15) даёт отклонение от положения равновесия точки с радиус-вектором в момент времени t. Для того, чтобы представить зависимость от координат и времени в явном виде необходимо учесть, что Теперь уравнение плоской волны принимает вид: Часто оказывается полезным представить уравнение волны в экспоненциальной форме. Для этого воспользуемся формулой Эйлера: где , запишем уравнение (22.15) в виде: Волновое уравнение Уравнение любой волны является решением дифференциального уравнения второго порядка, называемого волновым. Для того чтобы установить вид этого уравнения, найдем вторые производные по каждому из аргументов уравнения плоской волны (22.17): 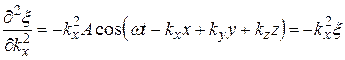 , (22.20) , (22.20)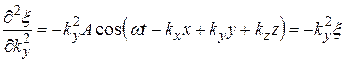 , (22.21) , (22.21)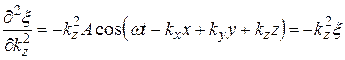 , (22.22) , (22.22)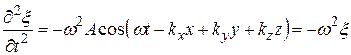 . 22.23) . 22.23)Сложим первые три уравнения с производными по координатам: 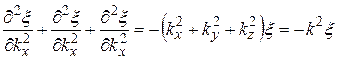 . (22.24) . (22.24)Выразим из уравнения (22.23) : 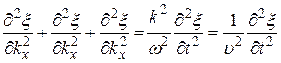 (22.25) (22.25)Сумму вторых производных в левой части (22.25) представим как результат действия оператора Лапласа на , и в окончательном виде представим волновое уравнение в виде: 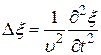 (22.26) (22.26)Примечательно, что в волновом уравнении квадратный корень из величины, обратной коэффициенту при производной по времени дает скорость распространения волны. Можно показать, что волновому уравнению (22.26) удовлетворяет любая функция вида: и каждая из них является уравнением волны и описывает некоторую волну. Энергия упругой волны Рассмотрим в среде, в которой распространяется упругая волна (22.10), Вследствие распространения в среде волны объём обладает энергией упругой деформации 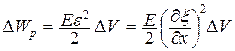 (22.38) (22.38)В соответствии с (22.35) модуль Юнга можно представить в виде . Поэтому: 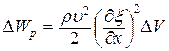 . (22.39) . (22.39)Рассматриваемый объём обладает также кинетической энергией: 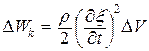 . (22.40) . (22.40)Полная энергия объёма: 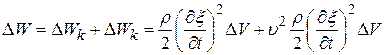 . (22.41) . (22.41)А плотность энергии: 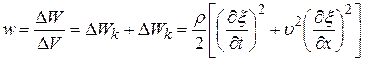 . (22.42) . (22.42)Но Подставим эти выражения в (22.42) и учтем, что : Таким образом, плотность энергии различна в разных точках пространства и меняется во времени по закону квадрата синуса. Среднее значение квадрата синуса равно 1/2, а значит среднее по времени значение плотности энергии в каждой точке среды, в которой распространяется волна: 12. Уравнение состояния идеального газа. Изопроцессы. Соотношение
связывающее давление газа с его температурой и концентрацией молекул, получено в 2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
Здесь N – число молекул в сосуде, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:
Соотношение
называется уравнением состояния идеального газа. Для одного моля любого газа это соотношение принимает вид:
Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный
Это утверждение называется законом Авогадро. Для смеси невзаимодействующих газов уравнение состояния принимает вид
где ν1, ν2, ν3 и т. д. – количество вещества каждого из газов в смеси. Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном, в форме (*) оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева. Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории. Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние. Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами. |
