1. основные понятия надёжности технических систем

• Название: 1. основные понятия надёжности технических систем
• Анкор: referat
• Дата: 09.11.2020
• Размер: 364.88 Kb.
• Имя файла: shubin_removed_removed.docx
• Тип: Документы; #148961
• страница: 4 из 9

Контрольные вопросы

1. 
   Дать анализ кривой интенсивности отказов.
   
2. 
   Дать определение статистической интенсивности отказов.
   
3. 
   Дать определение среднему времени безотказной работы.
   
4. 
   Дать определение средней наработке до отказа.
   
5. 
   Дать понятие среднему времени жизни изделия.
   
6. 
   Дать определение коэффициента оперативной готовности.
   
7. 
   Дать определение безотказности.
   
8. 
   Дать понятие коэффициента технического использования.
   

4. РАСЧЁТ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ ТЕХНИЧЕСКИХ СИСТЕМ

1. 
   СТРУКТУРНЫЕ МОДЕЛИ НАДЁЖНОСТИ СЛОЖНЫХ СИСТЕМ Большинство технических систем являются сложными системами,
   

состоящими из отдельных узлов, деталей, агрегатов, систем управления и т.п. Под сложной системой понимается объект, предназначенный для выполнения заданных функций, который может быть расчленён на эле- менты (компоненты), каждый из которых также выполняет определённые функции и находится во взаимодействии с другими элементами системы.

С позиций надёжности сложная система обладает как отрицательны- ми, так и положительными свойствами.

Факторы, отрицательно влияющие на надёжность сложных систем, следующие:

• 
  во-первых, это большое число элементов, отказ каждого из кото- рых может привести к отказу всей системы;
  
• 
  во-вторых, оценить работоспособность сложных систем весьма затруднительно с точки зрения статистических данных, так как они часто являются уникальными или имеются в небольших количествах;
  
• 
  в-третьих, даже у систем одинакового предназначения каждый экземпляр имеет свои незначительные вариации свойств отдельных эле- ментов, что сказывается на выходных параметрах системы. Чем сложнее система, тем большими индивидуальными особенностями она обладает.
  

Однако сложные системы обладают и такими свойствами, которые положительно влияют на их надёжность:

• 
  во-первых, сложным системам свойственна самоорганизация, са- морегулирование или самоприспособление, когда система способна найти наиболее устойчивое для своего функционирования состояние;
  
• 
  во-вторых, для сложной системы часто возможно восстановление работоспособности по частям без прекращения её функционирования;
  
• 
  в-третьих, не все элементы системы одинаково влияют на надёж- ность сложной системы.
  

Анализ работоспособности сложной системы связан с изучением её структуры и тех взаимосвязей, которые определяют её надёжное функ- ционирование.

При анализе надёжности сложных систем их разбивают на элементы (компоненты) с тем, чтобы вначале рассмотреть параметры и характери- стики элементов, а затем оценить работоспособность всей системы. Под элементом можно понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными па- раметрами. При исследовании надёжности системы элемент не расчленя- ется на составные части, и показатели безотказности и долговечности от-

носятся к элементу в целом. При этом возможно восстановление работо- способности элемента независимо от других частей и элементов системы.

Анализ надёжности сложных систем имеет свои специфические осо- бенности. Влияние различных отказов и снижение работоспособности элементов системы по-разному скажутся на надёжности всей системы.

При анализе надёжности сложной системы все её элементы и компо- ненты целесообразно разделить на следующие группы:

1. 
   элементы, отказ которых практически не влияет на работоспособ- ность системы (деформация ограждающего кожуха машины, изменение окраски поверхности и т.п.). Отказы (т.е. неисправное состояние) этих элементов могут рассматриваться изолированно от системы;
   
2. 
   элементы, работоспособность которых за рассматриваемый пери- од времени практически не изменяется (станины и корпусные детали, ма- лонагруженные элементы с большим запасом прочности);
   
3. 
   элементы, ремонт или регулировка которых возможна при работе изделия или во время остановок, не влияющих на его эффективность (подналадка и замена режущего инструмента на станке, регулировка хо- лостого хода карбюратора автомобильного двигателя);
   
4. 
   элементы, отказ которых приводит к отказам системы.
   

2. 
   СТРУКТУРНАЯ СХЕМА НАДЁЖНОСТИ СИСТЕМЫ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
   

Структурные схемы надёжности системы с последовательным со- единением элементов (рис. 7) – это случай, когда отказ одного элемента вызывает отказ другого элемента, а затем третьего и т.д. Например, боль- шинство приводов машин и механизмы передач подчиняются этому усло- вию. Так, если в приводе машины выйдет из строя любая шестерня, под- шипник, муфта, рычаг управления, электродвигатель, насос смазки, то весь привод перестанет функционировать. При этом отдельные элементы в этом приводе не обязательно должны быть соединены последовательно.

Такую структурную схему называют схемой с последовательным со- единением зависимых элементов. В этом случае надёжность системы оп- ределяют по теореме умножения для зависимых событий.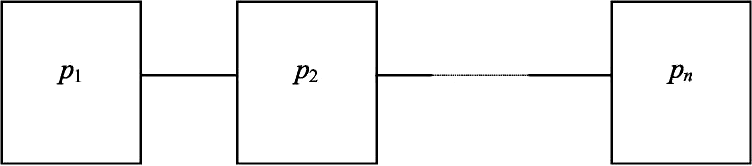




Рис. 7. Структурная схема надёжности системы с последовательным соединением элементов

Рассмотрим систему, состоящую из двух или более элементов. Пусть А – событие, состоящее в том, что система работает безотказно, a A_i(i = 1, 2, ..., п) – события, состоящие в исправной работе всех её элемен- тов. Далее предположим, что событие А имеет место тогда и только тогда, когда имеют место все события A_i, т.е. система исправна тогда и только тогда, когда исправны все её элементы. В этом случае систему называют последовательной системой.

Известно, что отказ любого элемента такой системы приводит, как правило, к отказу системы. Поэтому вероятность безотказной работы системы определяют как произведение вероятностей для независимых событий.


n

Таким образом, надёжность всей системы равна произведению на- дёжностей подсистем или элементов:
P( A)  _P( A_i ) ;

i1

где Р – надёжность.


P  _ p_i ,

i1

Сложные системы, состоящие из элементов высокой надёжности, могут обладать низкой надёжностью за счёт наличия большого числа эле- ментов. Например, если узел состоит всего из 50 деталей, а вероятность безотказной работы каждой детали за выбранный промежуток времени составляет р_i= 0,99, то вероятность безотказной работы узла будет P(t) =

= (0,99)⁵⁰ = 0,55.

Если же узел с аналогичной безотказностью элементов состоит из 400 деталей, то P(t) = (0,99)⁴⁰⁰ = 0,018, т.е. узел становится практически неработоспособным.

3. 
   СТРУКТУРНЫЕ СХЕМЫ НАДЁЖНОСТИ СИСТЕМ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
   

В практике проектирования сложных технических систем часто ис- пользуют схемы с параллельным соединением элементов (рис. 8), которые построены таким образом, что отказ системы возможен лишь в случае, когда отказывают все её элементы, т.е. система исправна, если исправен хотя бы один её элемент. Такое соединение часто называют резервирова- нием. В большинстве случаев резервирование оправдывает себя, несмотря на увеличение стоимости. Наиболее выгодным является резервирование отдельных элементов, которые непосредственно влияют на выполнение основной работы. При конструировании технических систем в зависимо-

Рис. 8. Структурная схема надёжности системы с параллельным соединением элементов
сти от выполняемой системой задачи применяют горячее или холодное резервирование.

Горячее резервирование применяют тогда, когда не допускается пе- рерыв в работе на переключение отказавшего элемента на резервный с целью выполнения задачи в установленное время. Чаще всего горячему резервированию подвергают отдельные элементы. Используют горячее резервирование элементов и подсистем, например источников питания (аккумуляторные батареи дублируются генератором и т.п.).

Холодное резервирование используют в тех случаях, когда необходи- мо увеличение ресурса работы элемента, и поэтому предусматривают время на переключение отказавшего элемента на резервный.

Существуют технические системы с частично параллельным резер- вированием, т.е. системы, которые оказываются работоспособными даже в случае отказа нескольких элементов.

Рассмотрим систему, имеющую ряд параллельных элементов с на- дёжностью p(t) и соответственно ненадёжностью q(t) = 1 – p(t). В случае если система содержит п элементов, которые соединены параллельно, вероятность отказа системы равна

Q  [ q (t)]ⁿ,

а вероятность безотказной работы

P(t)  1[ q (t)]ⁿ.

При частично параллельном резервировании вероятность безотказ- ной работы системы, состоящей из общего числа элементов n, определяют по формуле

P(t) 