36
Контрольные вопросы
Дать определение системы «человек–машина».
Что такое СЧМ дискретного типа?
Дать понятие показателю восстанавливаемости.
Что такое вероятность выполнения задачи.
Охарактеризовать величину – надёжность деятельности оператора.
Дать определение показателю надёжности.
Указать основной показатель своевременности.

ЛОГИКО-ГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА НАДЁЖНОСТИ И РИСКА
Анализ причин промышленных аварий показывает, что возникнове- ние и развитие крупных аварий, как правило, характеризуется комбинаци- ей случайных локальных событий, возникающих с различной частотой на разных стадиях аварии (отказы оборудования, человеческие ошибки при эксплуатации проектировании, внешние воздействия, разрушение, раз- герметизация, выброс, утечка, пролив вещества, испарение, рассеяние веществ, воспламенение, взрыв, интоксикация и т.д.). Для выявления при- чинно-следственных связей между этими событиями используют логико- графические методы деревьев отказов и событий.
Модели процессов в человеко-машинных системах должны отражать процесс появления отдельных предпосылок и развития их в причинную цепь происшествия в виде соответствующих диаграмм причинно- следственных связей – диаграмм влияния. Такие диаграммы являются формализованными представлениями моделируемых объектов, процессов, целей, свойств в виде множества графических символов (узлов, вершин) и отношений – предполагаемых или реальных связей между ними. Широкое распространение получили диаграммы в форме потоковых графов (гра- фов состояний и переходов), деревьев событий (целей, свойств) и функ- циональных сетей различного предназначения и структуры.
В последние десятилетия интенсивно разрабатываются диаграммы влияния из класса семантических или функциональных сетей, которые являются графами, но с дополнительной информацией, содержащейся в их узлах и дугах (рёбрах). Достоинства таких сетей: возможность объеди- нения логических и графических способов представления исследуемых процессов, учёт стохастичности информации, выраженной узлами и дуга- ми, доступность для моделирования циклических и многократно наблю- даемых событий, наибольшие (по сравнению с другими типами диаграмм) логические возможности.
Другим (после графов) и наиболее широко используемым типом диа- грамм влияния являются «деревья». В безопасности диаграммы данного класса часто называют «деревом происшествий» и «деревом их исходов». Они являются в сущности графами с ветвящейся структурой и с дополни- тельными (логическими) условиями.
Основные достоинства этих моделей: сравнительная простота по- строения; дедуктивный характер выявления причинно-следственных свя- зей исследуемых явлений; направленность на их существенные факторы; лёгкость преобразования таких моделей; наглядность реакции изучаемой системы на изменение структуры; декомпозируемость «дерева» и процес- са его изучения; возможность качественного анализа исследуемых про- цессов; лёгкость дальнейшей формализации и алгоритмизации; приспо-
собленность к обработке на средствах ВТ; доступность для статистиче- ского моделирования и количественной оценки изучаемых явлений, про- цессов и их свойств.
Создание дерева заключается в определении его структуры:
а) элементов – головного события (происшествия) и ему предшест- вующих предпосылок;
б) связей между ними – логических условий, соблюдение которых необходимо и достаточно для его возникновения.
На практике обычно используют обратную или прямую последова- тельность выявления условий возникновения конкретных происшествий или аварийности и травматизма в целом:
от головного события дедуктивно к отдельным предпосылкам;
от отдельных предпосылок индуктивно к головному событию.
Из анализа структуры диаграммы влияния следует, что основными её компонентами служат узлы (вершины) и связи (отношения) между ними. В качестве узлов обычно подразумеваются простейшие элементы модели- руемых категорий (переменные или константы) – события, состояния, свойства, а в качестве связей – активности, работы, ресурсы и другие взаимодействия. Отношения или связи между переменными или констан- тами в узлах диаграммы графически представляются в виде линий, назы- ваемых дугами или рёбрами.
Каждые два соединённых между собой узла образуют ветвь диа- граммы. В тех случаях, когда узлы связаны направленными дугами таким образом, что каждый из них является общим ровно для двух ветвей, воз- никают циклы или петли.
Переменные в узлах характеризуются фреймами данных – множест- вом выходов (значений, принимаемых переменными, неизменных во вре- мени и между собой не пересекающихся) и условными распределениями вероятностей появления каждого из них.
Идея прогнозирования размеров ущерба от происшествий в челове- ко-машинных системах основана на использовании деревьев специально- го типа (деревьев исходов) – вероятностных графов. Их построение по- зволяет учитывать различные варианты разрушительного воздействия потоков энергии или вредного вещества, высвободившихся в результате происшествия.
С помощью предварительно построенных диаграмм – графов, сетей и деревьев могут быть получены математические модели аварийности и травматизма.
В исследовании безопасности широкое распространение получили диаграммы влияния ветвящейся структуры, называемые «деревом» собы- тий (отказов, происшествий). Деревом событий называют не ориентиро- ванный граф, не имеющий циклов, являющийся конечным и связным. В нём каждая пара вершин должна быть связанной (соединённой цепью),
однако все соединения не должны образовывать петель (циклов), т.е. со- держать такие маршруты, вершины которых одновременно являются на- чалом одних и концом других цепей.
Структура дерева происшествий обычно включает одно размещаемое сверху нежелательное событие – происшествие (авария, несчастный случай, катастрофа), которое соединяется с набором соответствующих событий – предпосылок (ошибок, отказов, неблагоприятных внешних воздействий), образующих определённые их цепи или «ветви». «Листья- ми» на ветвях дерева происшествий служат предпосылки – инициаторы причинных цепей, рассматриваемые как постулируемые исходные собы- тия, дальнейшая детализация которых нецелесообразна. В качестве узлов дерева происшествий могут использоваться как отдельные события или состояния, так и логические условия их объединения (сложения или пе- ремножения).
ПРОЦЕДУРА АНАЛИЗА «ДЕРЕВА ОТКАЗОВ»
Опасности носят потенциальный, т.е. скрытый характер. Условия реализации потенциальной опасности называются причинами.
Опасность – следствие некоторой причины или группы причин, ко- торая, в свою очередь, является следствием другой причины, т.е. причины и следствия образуют иерархические структуры или системы, так назы- ваемые: «дерево событий», «дерево причин», «дерево отказа» или «дерево опасности», «дерево неисправностей».
Процедура построения дерева неисправностей (отказов) включает, как правило, следующие этапы:
Определение нежелательного (завершающего) события в рас- сматриваемой системе.
Тщательное изучение возможного поведения и предполагаемого режима использования системы.
Определение функциональных свойств событий более высокого уровня для выявления причин тех или иных неисправностей системы и проведение более глубокого анализа поведения системы с целью выявле- ния логической взаимосвязи событий более низкого уровня, способных привести к отказу системы.
Построение дерева неисправностей (отказов) для логически свя- занных событий на входе. Эти события должны определяться в терминах идентифицируемых независимых первичных отказов. Чтобы получить количественные результаты для завершающего нежелательного события дерева, необходимо задать вероятность отказа, коэффициент неготовно- сти, интенсивность отказов, интенсивность восстановлений и другие по- казатели, характеризующие первичные события, при условии, что собы- тия дерева неисправностей не являются избыточными.
Более строгий и систематический анализ предусматривает выполне- ние таких процедур, как (1) определение границ системы, (2) построение дерева неисправностей, (3) качественная оценка, (4) количественная оценка. Обычно система изображается в виде блок-схемы, показывающей все функциональные взаимосвязи и элементы. При построении дерева неис- правностей исключительно важную роль приобретает правильное задание граничных условий, которые не следует путать с физическими границами
системы.
Одним из основных требований, предъявляемых к граничным усло- виям, является задание завершающего нежелательного события, установ- ление которого требует особой тщательности, поскольку именно для него как для основного отказа системы строится дерево неисправностей. Кроме того, чтобы проводимый анализ был понятен всем заинтересованным ли- цам, исследователь обязан составить перечень всех допущений, прини- маемых при определении системы и построении дерева неисправностей.
Анализ дерева происшествий связан с определением возможности появления или непоявления головного события – происшествия конкрет- ного типа. Данные условия устанавливаются путём выделения из всего массива исходных предпосылок двух подмножеств, реализация которых либо приводит, либо не приводит к возникновению головного события. Такие подмножества делятся на аварийные сочетания предпосылок, обра- зующие в совокупности с условиями их появления каналы прохождения сигнала до этого события, и отсечные сочетания, исключающие условия формирования таких путей к головному событию. Самым удобным спо- собом выявления условий возникновения и предупреждения происшест- вий является выделение из таких подмножеств так называемых «мини- мальных сочетаний событий», т.е. тех из них, появление которых мини- мально необходимо и достаточно для достижения желаемого результата.
ПОСТРОЕНИЕ «ДЕРЕВА ОТКАЗОВ»
Дерево отказов – это топологическая модель надёжности и безопас- ности, которая отражает логико-вероятностные взаимосвязи между от- дельными случайными исходными событиями в виде первичных отказов или результирующих отказов, совокупность которых приводит к главному анализируемому событию. Таким образом, «дерево отказов» – это ориен- тировочный граф в виде дерева.
Основной целью построения дерева неисправностей является симво- лическое представление существующих в системе условий, способных вызвать её отказ. Кроме того, построенное дерево позволяет показать в явном виде слабые места системы и является наглядным средством пред- ставления и обоснования принимаемых решений, а также средством ис-
следования компромиссных соотношений или установления степени со- ответствия конструкции системы заданным требованиям.
Выделяют пять типов вершин «дерева отказов» (ДО):
вершины, отображающие первичные отказы;
вершины, отображающие результирующие или вторичные отказы;
вершины, отображающие локальные отказы, которые не влияют на возникновение других отказов;
вершины, соответствующие операции логического объединения случайных событий (типа «ИЛИ»);
вершины, соответствующие операции логического произведения случайных событий (типа «И»).
Каждой вершине ДО, отображающей первичный или результирую- щий отказ, соответствует определенная вероятность возникновения отка- за. Одним из основных преимуществ ДО является то, что анализ ограни- чивается выявлением только тех элементов систем и событий, которые приводят к постулируемому отказу или аварии. Чтобы определить вероят- ность отказа, необходимо найти аварийные сочетания, для чего необходимо произвести качественный и количественный анализ «дерева отказов».
Структура «дерева отказа» включает одно головное событие (ава- рию, инцидент), которое соединяется с набором соответствующих ниже- стоящих событий (ошибок, отказов, неблагоприятных внешний воздейст- вий), образующих причинные цепи (сценарии аварий). Для связи между событиями в узлах «деревьев» используются знаки «И» и «ИЛИ». Логиче- ский знак «И» означает, что вышестоящее событие возникает при одно- временном наступлении нижестоящих событий (соответствует перемно- жению их вероятностей для оценки вероятности вышестоящего события). Знак «ИЛИ» означает, что вышестоящее событие может произойти вслед- ствие возникновения одного из нижестоящих событий.
Обычно предполагается, что исследователь, прежде чем приступить к построению дерева неисправностей, тщательно изучает систему. Поэто- му описание системы должно быть частью документации, составленной в ходе такого изучения.
В зависимости от конкретных целей анализа дерева неисправностей для построения последнего специалисты по надёжности обычно исполь- зуют либо метод первичных отказов, либо метод вторичных отказов, либо метод инициированных отказов.
Метод первичных отказов. Отказ элемента называется первичным, если он происходит в расчётных условиях функционирования системы. Построение дерева неисправностей на основе учёта лишь первичных от- казов не представляет большой сложности, так как дерево строится толь- ко до той точки, где идентифицируемые первичные отказы элементов вы- зывают отказ системы. Для иллюстрации этого метода рассмотрим сле- дующий пример.
Метод вторичных отказов. Чтобы анализ охватывал и вторичные отказы, требуется более глубокое исследование системы. При этом анализ выходит за рамки рассмотрения системы на уровне отказов её основных элементов, поскольку вторичные отказы вызываются неблагоприятным воздействием окружающих условий или чрезмерными нагрузками на эле- менты системы в процессе эксплуатации.
Метод инициированных отказов. Подобные отказы возникают при правильном использовании элемента, но в неустановленное время или в неположенном месте. Другими словами, инициированные отказы – это сбои операций координации событий на различных уровнях дерева неис- правностей: от первичных отказов до завершающего события (нежела- тельного либо конечного).
КАЧЕСТВЕННАЯ И КОЛИЧЕСТВЕННАЯ ОЦЕНКА
«ДЕРЕВА ОТКАЗОВ»
Излагаемый ниже подход основан на использовании так называемых минимальных сечений дерева неисправностей.
Сечение определяется как множество элементарных событий, приво- дящих к нежелательному исходу. Если из множества событий, принадле- жащих некоторому сечению, нельзя исключить ни одного и в то же время это множество событий приводит к нежелательному исходу, то в этом случае говорят о наличии минимального сечения. Выявление минималь- ных сечений требует больших затрат времени, и для их нахождения тре- буется машинный алгоритм. Пример качественной оценки «дерева отка- зов» представлен на рис. 11.
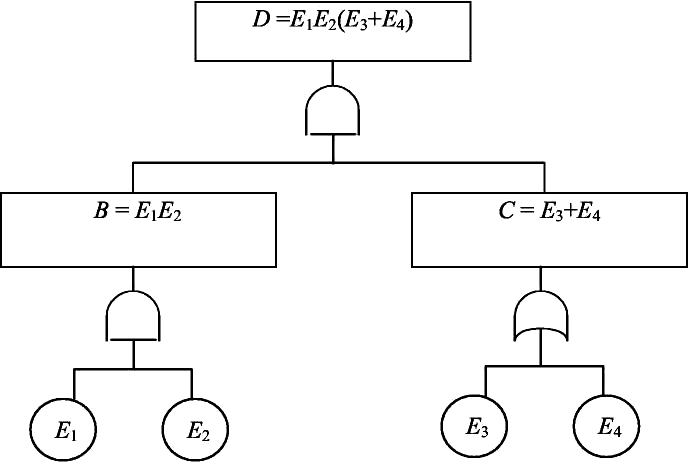
Рис. 11. «Дерево отказов»
Количественная оценка производится на основании информации о таких количественных показателях надёжности для завершающего собы- тия, как вероятность отказа, интенсивность отказов или интенсивность восстановлений. Вначале вычисляют показатели надёжности элемента, затем находят критический путь и, наконец, оценивают завершающее событие.
Количественная оценка дерева осуществляется либо методом стати- ческого моделирования, либо аналитическим методом.
В первом случае дерево неисправностей моделируется на ЭВМ обычно для нескольких тысяч или даже миллионов циклов функциониро- вания системы. При этом основными этапами моделирования являются:
задание показателей надёжности для элементарных событий;
представление всего дерева неисправностей на цифровой ЭВМ;
составление перечня отказов, приводящих к завершающему со- бытию, и перечня соответствующих минимальных сечений;
вычисление требуемых конечных результатов.
Во втором случае используют существующие аналитические методы.
АНАЛИТИЧЕСКИЙ ВЫВОД ДЛЯ ПРОСТЫХ СХЕМ
«ДЕРЕВА ОТКАЗОВ»
Для того чтобы дерево неисправностей отвечало своему назначению, в нём используются схемы, показывающие логические связи между отка- зами основных элементов системы и завершающим событием. Для пред- ставления этих логических схем в математической форме применяются основные законы булевой алгебры.
Схема «ИЛИ» изображается символом или +. Любой из этих сим- волов показывает объединение событий, связанных со схемой «ИЛИ». Математическое описание схем «ИЛИ» с двумя событиями на входе дано на рис. 12.
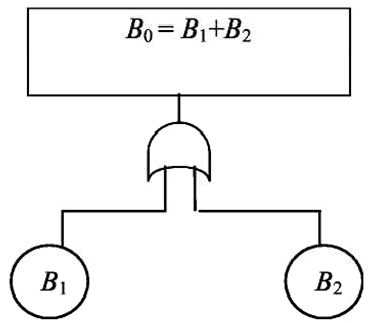
Рис. 12. Схема «ИЛИ» с двумя выходами
как
Событие В0 на выходе схемы «ИЛИ» записывается в булевой алгебре
B0 B1 B2 ,
где В1 и В2 – события на входе. Схема « И» изображается символом * или ∩. Этот символ обозначает пересечение событий. Схема « И» с двумя входами показана на рис. 13. Событие В0 на выходе схемы « И» записывается в булевой алгебре как B0 B1B2 . Схема « И» с приоритетом логически эквивалентна схеме « И», но от- личается от неё тем, что события на её входе должны происходить в опре- делённом порядке. Схема « И» с приоритетом, имеющая два входа, пока- зана на рис. 14. В данном случае предполагается, что событие А1 должно наступить раньше события А2. 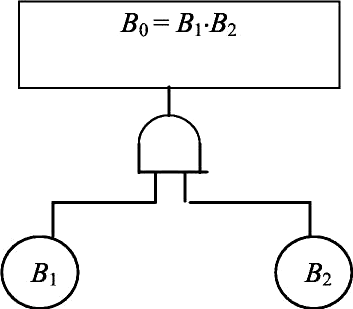 Рис. 13. Схема «И» с двумя входами Рис. 13. Схема «И» с двумя входами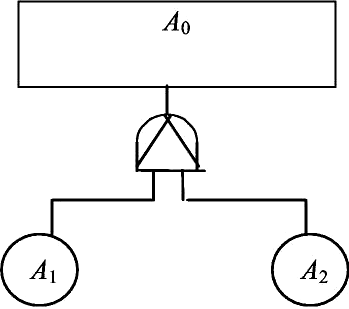 Рис. 14. Приоритетная схема «И» с двумя входами Рис. 14. Приоритетная схема «И» с двумя входами
«ДЕРЕВО ОТКАЗОВ» С ПОВТОРЯЮЩИМИСЯ СОБЫТИЯМИ
Характерная конфигурация такого дерева неисправностей показана на рис. 15.
В этом случае «дерево неисправностей» можно представить с помо- щью следующих булевых выражений:
T CB0 ,
B0 B1B2 ,
B1 A1 A2 ;
B2 A1 A3 ,
где A1, A2, A3 и С – элементарные события; В1, В2, В0 – промежуточные события; Т – завершающее событие. Подставляя в первое выражение соотношения для В0, В1 и В2, по- лучаем T C( A1 A2 ) ( A1 A3 ) . 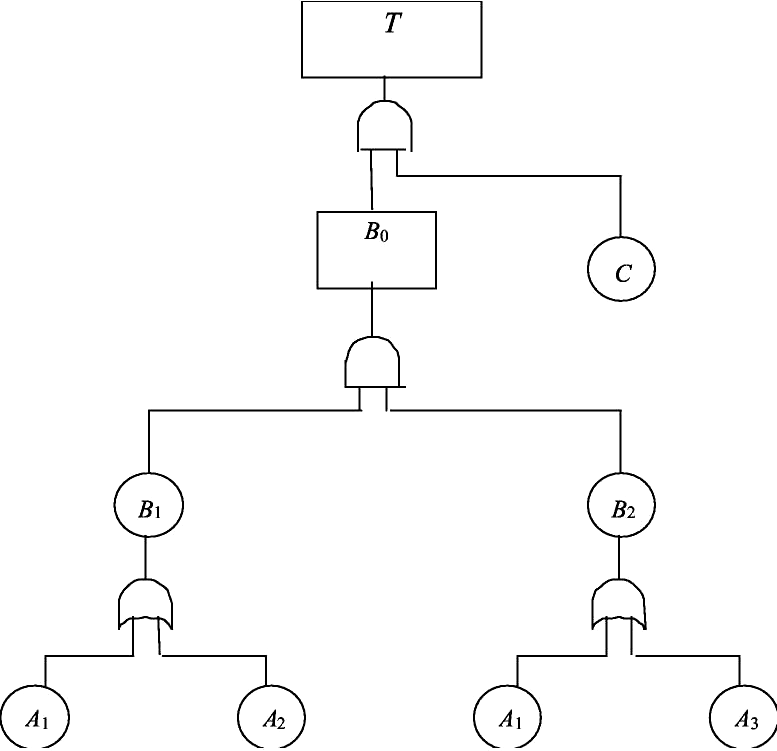 Рис. 15. «Дерево отказов» в случае повторяющихся событий Рис. 15. «Дерево отказов» в случае повторяющихся событий
Согласно рис. 15, отказ А1 является повторяющимся элементарным событием, поэтому полученное выражение необходимо упростить, ис- пользуя распределительный закон булевой алгебры.
В результате получаем
T C [ A1 A2 A3 ] ,
и первоначальное «дерево неисправностей» (рис. 15) принимает вид, по- казанный на рис. 16.
Таким образом, прежде чем находить количественные показатели надёжности и риска, следует упростить выражения с повторяющимися событиями, используя свойства булевой алгебры, в противном случае бу- дут получены ошибочные количественные оценки.
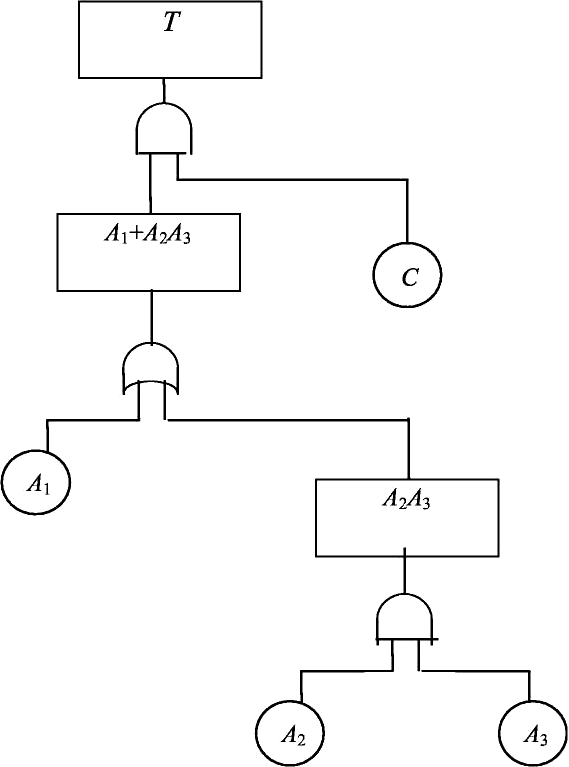
Рис. 16. Упрощённое «дерево неисправностей»
ПРЕИМУЩЕСТВА И НЕДОСТАТКИ МЕТОДА «ДЕРЕВА ОТКАЗОВ»
Данный метод, как и любой другой, обладает определёнными досто- инствами и недостатками. Так, например, метод даёт представление о по- ведении системы, но требует от специалистов по надёжности глубокого понимания системы и конкретного рассмотрения каждый раз только од- ного определённого отказа; помогает дедуктивно выявлять отказы; даёт конструкторам, пользователям и руководителям возможность наглядного обоснования конструктивных изменений и анализа компромиссных реше- ний; позволяет выполнять количественный и качественный анализ надёж- ности; облегчает анализ надёжности сложных систем. Вместе с тем реали- зация метода требует значительных затрат средств и времени. Кроме того, полученные результаты трудно проверить и трудно учесть состояния час- тичного отказа элементов, поскольку при использовании метода, как пра- вило, считают, что система находится либо в исправном состоянии, либо в состоянии отказа. Существенные трудности возникают и при получении в общем случае аналитического решения для деревьев, содержащих резерв- ные узлы и восстанавливаемые узлы с приоритетами, не говоря уже о тех значительных усилиях, которые требуются для охвата всех видов множе- ственных отказов.
|
 Скачать 364.88 Kb.
Скачать 364.88 Kb.