1. основные понятия надёжности технических систем

• Название: 1. основные понятия надёжности технических систем
• Анкор: referat
• Дата: 09.11.2020
• Размер: 364.88 Kb.
• Имя файла: shubin_removed_removed.docx
• Тип: Документы; #148961
• страница: 2 из 9

ЗАКОНЫ РАСПРЕДЕЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В ТЕОРИИ НАДЁЖНОСТИ

1. 
   ЗАКОН РАСПРЕДЕЛЕНИЯ ПУАССОНА
   

Закон распределения Пуассона описывает закономерность появления случайных отказов в сложных системах. Этот закон нашёл широкое применение при определении вероятности появления и восстановления отказов.

Случайная величина Х распределена по закону Пуассона, если веро- ятность того, что эта величина примет определённое значение т, выража- ется формулой

^m 

P_m  _m! e ,

где λ – параметр распределения (некоторая положительная величина); m = 0, 1, 2, 3, …, п математическое ожидание M_xи дисперсия D_xслучай- ной величины Х для закона Пуассона равны параметру распределения λ:

M _x  D_x   .

Распределение Пуассона является однопараметрическим с пара- метром λ.

2. 
   ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Экспоненциальный закон распределения, называемый также основ-
   

ным законом надёжности, часто используют для прогнозирования надёж- ности в период нормальной эксплуатации изделий, когда постепенные отказы ещё не проявились и надёжность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность. Экспонен- циальное распределение находит довольно широкое применение в теории массового обслуживания, описывает распределение наработки на отказ сложных изделий, время безотказной работы элементов радиоэлектрон- ной аппаратуры.

Приведём примеры неблагоприятного сочетания условий работы де- талей машин, вызывающих их внезапный отказ. Для зубчатой передачи это может быть действием максимальной нагрузки на наиболее слабый зуб при его зацеплении; для элементов радиоэлектронной аппаратуры – превышение допустимого тока или температурного режима. Плотность распределения экспоненциального закона (рис. 1) описывается соотноше- нием

f (x)  t ^x;

функция распределения этого закона – соотношением

F (x)  1 e^x;

функция надёжности

P(x)  1  F (x)  e^x;

математическое ожидание случайной величины Х



M _x  _ xe

0

дисперсия случайной величины Х
x

dx  ¹ ;




2 x ^{1 1}

D_x  _ x e

0

dx  _2  _2 .

Экспоненциальный закон в теории надёжности нашёл широкое при- менение, так как он прост для практического использования. Почти все задачи, решаемые в теории надёжности, при использовании экспоненци- ального закона оказываются намного проще, чем при использовании дру- гих законов распределения. Основная причина такого упрощения состоит в том, что при экспоненциальном законе вероятность безотказной работы зависит только от длительности интервала и не зависит от времени пред- шествующей работы.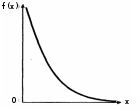




Рис. 1. График плотности экспоненциального распределения

3. 
   НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
   

Нормальный закон распределения часто называют законом Гаусса. Этот закон играет важную роль и наиболее часто используется на практи- ке по сравнению с другими законами распределения.

Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распреде- ления. В теории надёжности его используют для описания постепенных отказов, когда распределение времени безотказной работы вначале имеет низкую плотность, затем максимальную и далее плотность снижается.

Распределение всегда подчиняется нормальному закону, если на из- менение случайной величины оказывают влияние многие, примерно рав- нозначные факторы.

Нормальный закон распределения описывается следующей зависи- мостью:

f (x) 

_ ( xm)<sup>2

1</sup> _e 2² _,

где е = 2,71828 – основание натурального логарифма; π= 3,14159; т и σ –

параметры распределения, определяемые по результатам испытаний.

Кривая плотности распределения приведена на рис. 2.

Параметр т = М_xпредставляет собой среднее значение случайной величины X, оцениваемое по формуле

₁ n


n
M_x _ x_i ;

i1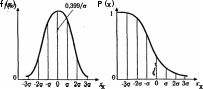




а) б)

Рис. 2. Кривые плотности вероятности (а) и функции надёжности (б)

нормального распределения

параметр σ – среднее квадратическое отклонение случайной величины X,

оцениваемое по формуле
 

;
вероятность отказа и вероятность безотказной работы

_{x x } ( xm)²

F (x)  _ f (x) dx  ¹ _ e ^22

dx ;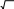

 ^

2 _

соответственно Q(x) =F(x), Р(х) =1 – F(x).

Вычисление интегралов заменяют использованием таблиц нормаль- ного распределения, при котором М_x = 0 и σ = 1. Для этого распределения функция плотности вероятности имеет одну переменную t и выражается зависимостью

f₀ (t) 

_{1  t} 2

e ² .

2

Величина t является центрированной (так как М_t= 0) и нормирован- ной (так как σ_t= 1). Функция распределения соответственно запишется в виде:

1
F₀ (t) 

t _ ^{t 2}

_ e ² dt .

2 _

Из этого уравнения следует, что 1F₀(t) + F₀(−t) = 1 или F₀(−t) =

= 1−F₀(t).

4. 
   ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Логарифмически нормальное распределение применяют дня описа-
   

ния наработки до отказа подшипников, электронных ламп и других изде- лий.

Неотрицательная случайная величина распределена логарифмически нормально, если её логарифм распределён нормально. Плотность распре- деления для различных значений σ приведена на рис. 3.

Плотность распределения описывается зависимостью

• 
  (ln xM)²
  

f (x) 

¹ _e 2² _,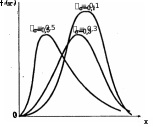

Рис. 3. Плотность логарифмически нормального распределения
где М и σ – параметры, оцениваемые по результатам п испытаний:

₁ n


n
M _ln x_i ;   .

i1

Для логарифмически нормального закона распределения функция надёжности выглядит так:

P(x)  ¹

 _ ^x2

_ e ² dx .

ln ( x / M )



Вероятность безотказной работы можно определить по таблицам для нормального распределения приложения

v  ^x 

x _M

e^2  1 .

x

Математическое ожидание наработки до отказа


x
_{M  e}(M ² / 2) _.

Среднее квадратическое отклонение
_x .

При v_x 0,3 полагают, что v_x= σ, при этом ошибка не более 1%.

Часто применяют запись зависимостей для логарифмически нор- мального закона в десятичных логарифмах. В соответствии с этим зако- ном плотность распределения

_{f (x) } 0,4343 _e

(lg xlg x₀ )²

2² _.

Оценки параметров lg x₀ и σ определяют по результатам испытаний:
₁ n


n
lg x₀  _ln x_i ;   .

i1

Математическое ожидание М_x, среднее квадратическое отклонение σ_xи коэффициент вариации v_xнаработки до отказа соответственно равны:


x 0
_{M  x e}2,65² _;
 _x  M_x ;

v_x .

5. 
   РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА
   

Закон Вейбулла представляет собой деухпараметрическое распреде- ление. Этот закон является универсальным, так как при соответствующих значениях параметров превращается в нормальное, экспоненциальное и другие виды распределений. Автор данного закона использовал его при описании экспериментально наблюдавшихся разбросов усталостной прочности стали, пределов её упругости. Закон Вейбулла удовлетвори- тельно описывает наработку до отказа подшипников, элементов радио- электронной аппаратуры, его используют для оценки надёжности деталей и узлов машин, в частности автомобилей, а также для оценки надёжности машин в процессе их приработки. Плотность распределения описывается зависимостью, график приведён на рис. 4.

f (x)  x^1 exp(x^ ) ,

где  – параметр формы кривой распределения;  – параметр масштаба.

Функция надёжности для этого закона:

Р(х) = ехр (–х^),

F(x) = 1 – exp (–х^).

Математическое ожидание случайной величины Х равно

M _x  Г(1 1/ ) ^{1/ 2} ,



Г(x)  _t ^x1e^t dt,

0
где Г(x) – гамма-функция для непрерывных значений х.

Дисперсия случайной величины Х равна

D_x  ^{2 / } [ Г(1  2 / )  Г(1  1/ )] .

Широкое применение закона распределения Вейбулла объясняется тем, что этот закон, обобщая экспоненциальное распределение, содержит дополнительный параметр . Подбирая нужным образом параметры  и , можно получить лучшее соответствие расчётных значений опытным дан- ным по сравнению с экспоненциальным законом, который является одно- параметрическим (параметр ).

Так, для изделий, у которых имеются скрытые дефекты, но которые длительное время не стареют, опасность отказа имеет наибольшее значе- ние в начальный период, а потом быстро падает. Функция надёжности для такого изделия хорошо описывается законом Вейбулла с параметром

 < 1.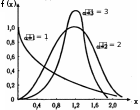





Рис. 4. Плотность распределения Вейбулла для  = 1

Наоборот, если изделие хорошо контролируется при изготовлении и почти не имеет скрытых дефектов, но подвергается быстрому старению, то функция надёжности описывается законом Вейбулла с параметром

 > 1. При  = 3,3 распределение Вейбулла близко к нормальному.