1. основные понятия надёжности технических систем

• Название: 1. основные понятия надёжности технических систем
• Анкор: referat
• Дата: 09.11.2020
• Размер: 364.88 Kb.
• Имя файла: shubin_removed_removed.docx
• Тип: Документы; #148961
• страница: 5 из 9

n


k  j

C^k p^k(t) q^nk(t) ,

где p(t) – вероятность безотказной работы одного элемента; j – число ис- правных элементов, при котором обеспечивается работоспособность сис- темы; С_n= n! / [k!(n – k)!] – число сочетаний из n элементов по k.

В случае j = 1 система будет полностью параллельной, в остальных случаях – частично параллельной.

4. 
   СТРУКТУРНЫЕ СХЕМЫ НАДЁЖНОСТИ СИСТЕМ С ДРУГИМИ ВИДАМИ СОЕДИНЕНИЯ ЭЛЕМЕНТОВ
   

Следует отметить, что в практике проектирования технических сис- тем часто используют структурные схемы надёжности с параллельно- последовательным соединением элементов. Так, например, часто при про- ектировании систем с радиоэлектронными элементами применяют схемы, работающие по принципу два из трёх, когда работоспособность обеспечи- вается благодаря исправному состоянию любых двух элементов. Надёж- ность такой схемы соединения определяют по формуле

P(t)  P³ (t)  3P ² (t) Q(t) ,

где p(t) – надёжность каждого элемента за время работы t одинакова;

q(t) = 1 – p(t).

Широкое применение в проектировании нашли так называемые мос- тиковые схемы. Надёжность такой схемы определяют из соотношения вида

P(t)  p⁵ (t)  5 p⁴ (t) q(t)  8 p³ (t) q² (t)  2 p² (t) q³ (t) .

Здесь все элементы также имеют одинаковую надёжность.



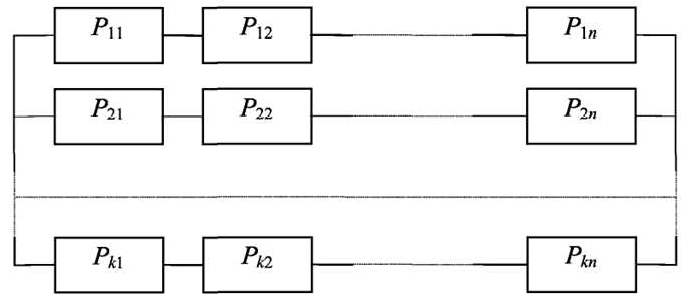Рис. 9. Структурная схема надёжности с поканальным резервированием

Различают структурные схемы надёжности с поканальным и поэле- ментным резервированием. Структурная схема надёжности с поканаль- ным резервированием показана на рис. 9.

Формула надёжности выглядит так:

P  [1 (1 p₁₁ p₁₂ ... p_1n ) (1 p₂₁ p₂₂ ... p_2n ) (1 p_k1 p_{k 2} ... p_kn ) ] .

При p_tj= p_j

Если p_ij= р, то

P 1 (1 p₁ p₂ ... p_n )^k.
P 1 (1 pⁿ)^k.

В практике проектирования часто используют структурную схему надёжности с поэлементным резервированием (рис. 10).

Надёжность такой системы определяют по формуле

P  [1 (1 p₁₁ ) (1 p₂₁ )...(1 p_k1 ) ] [ (1 p₁₂ ) (1 p₂₂ )...(1 p_{k 2} ) ]...

... [ (1 p_1n ) (1 p_2n )...(1 p_kn ) ] .

При p_ij= p_j

P [(1 p₁ )^k] [1(1 p₂ )^k]...[1 (1 p_n )^k] .

Если р_ij= p, то

P [(1 p)^k]ⁿ.

Анализ последних двух схем показывает, что структурная схема с поэлементным резервированием имеет более высокую надёжность по сравнению с поканальным резервированием.



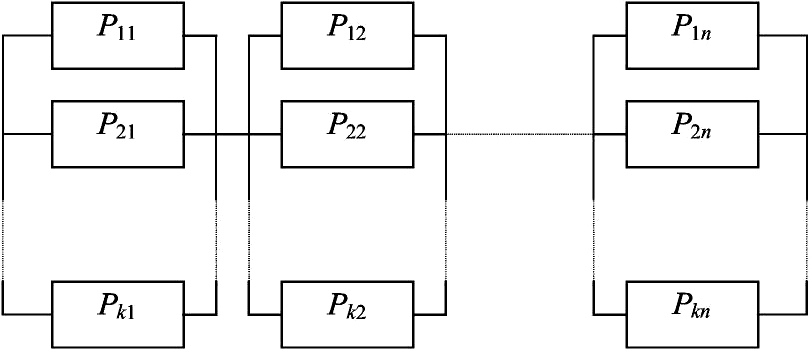Рис. 10. Структурная схема надёжности с поэлементным резервированием