1. основные понятия надёжности технических систем

• Название: 1. основные понятия надёжности технических систем
• Анкор: referat
• Дата: 09.11.2020
• Размер: 364.88 Kb.
• Имя файла: shubin_removed_removed.docx
• Тип: Документы; #148961
• страница: 3 из 9

Контрольные вопросы

1. 
   Перечислить модели распределения.
   
2. 
   В каком случае применимо распределение Вейбулла?
   
3. 
   В каком случае применим нормальный закон распределения?
   
4. 
   В каком случае применимо логарифмическое распределение?
   
5. 
   Перечислить основные показатели надёжности.
   
6. 
   Дать определение вероятности безотказной работы.
   
7. 
   Перечислить показатели безотказности.
   
8. 
   Перечислить показатели долговечности.
   
9. 
   Дать определение неремонтируемого изделия. Привести пример.
   
10. 
    Дать определение ремонтируемого изделия. Привести пример.
    
11. 
    В каком случае применим закон распределения Пуассона?
    
12. 
    В каком случае применим экспоненциальный закон распределения?
    
13. 
    В каком случае применим нормальный закон распределения?
    
14. 
    Дать определение интенсивности отказов.
    
15. 
    Дать определение математическому ожиданию.
    

3. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ НАДЁЖНОСТИ ЭЛЕМЕНТОВ И СИСТЕМ

   1. 
      ПОКАЗАТЕЛИ НАДЁЖНОСТИ НЕВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА
      

Невосстанавливаемым называют такой элемент, который после рабо- ты до первого отказа заменяют на такой же элемент, так как его восста- новление в условиях эксплуатации невозможно. В качестве примеров не- восстанавливаемых элементов можно назвать диоды, конденсаторы, триоды, микросхемы, гидроклапаны, пиропатроны и т.п.

Пусть время работы невосстанавливаемого элемента представляет собой случайную величину τ. В момент времени t = 0 элемент начинает работать, а в момент t = τ происходит его отказ, следовательно, τ является временем жизни элемента. Таким образом, τ имеет случайный характер, и в качестве основного показателя надёжности элемента можно назвать функцию распределения, которая выражается зависимостью

F (t)  P (  t ) .

Функцию F(t) называют также вероятностью отказа элемента до мо- мента t. Если элемент работает в течение времени t непрерывно, то суще- ствует непрерывная плотность вероятности отказа

f (t)  ^{dF (t)} .

dt

Следующим показателем надёжности является вероятность безотказ- ной работы за заданное время t или функция надёжности, которая явля- ется функцией, обратной функции распределения,

P(t)  1  F (t)  P (  t ) .

Графически функция надёжности представляет собой монотонно убывающую кривую (рис. 5; при t = 0 P(t = 0)= l; при t → ∞ P(t = ∞)= 0).

В общем виде вероятность безотказной работы испытуемых элемен- тов конструкций определяется как отношение числа элементов, остав- шихся исправными в конце времени испытания, к начальному числу эле- ментов, поставленных на испытание:

P(t)  (N  n) / N ,

где N – начальное число испытуемых элементов; п – число отказавших элементов за t; N – п = n₀ – число элементов, сохранивших работоспособ- ность.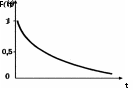



Рис. 5. Кривая функции надёжности
Важнейшим показателем невосстанавливаемого элемента является среднее время безотказной работы (Т₀), которое определяют по следую- щей зависимости:

_{T } ₁  ₂  ...  _n (N  n) t _.

0 _N
Следующей характеристикой надёжности невосстанавливаемого элемента является интенсивность отказов, или опасность отказа, которая определяет надёжность элемента в каждый данный момент времени. Ин- тенсивность отказа находят по формуле

(t)  f (t) / P(t)  [ dP(t) / dt]/ P(t)  P^(t) / P(t) .

Вероятность безотказной работы в интервале (t₁, t₂) выражается зави- симостью

_ ^t2 _

P(t)  exp _ _(t) dt _ .

^{ t}1 ^

Функция λ(t) может быть определена по результатам испытаний. Предположим, что испытаниям подвергают N элементов. Пусть n(t) – чис- ло элементов, не отказавших к моменту t. Тогда при достаточно малом ∆t и достаточно большом Nполучим

(t)  n /[t n(t)],

где ∆n – число отказов на участке ∆t.

Статистическая интенсивность отказов λ(t) равна отношению числа отказов, происшедших в единицу времени, к общему числу элементов, не отказавших к этому моменту времени.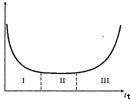

λ(t)

Рис. 6. Кривая интенсивности отказов
Многочисленные опытные данные показывают, что для многих эле- ментов функция λ(t) имеет следующий вид (рис. 6).

Анализ кривой интенсивности отказов показывает, что время испы- тания можно условно разбить на три периода. В первом из них функ- ция λ(t) имеет повышенные значения. Это период приработки или период ранних отказов для скрытых дефектов. Второй период называют перио- дом нормальной работы. Для этого периода характерна постоянная интен- сивность отказов. Последний третий период – это период старения. Так как период нормальной работы является основным, то в расчётах надёж- ности принимается λ(t) = λ = const. В этом случае при экспоненциальном законе распределения функция надёжности имеет вид

P(t)  exp(t ) .

Среднее время жизни соответственно равно



T₀  _exp (t) dt  1/  .

0

Если время работы элемента мало по сравнению со средним време- нем жизни, то можно использовать приближённую формулу

P(t)  1  t / T₀ .

2. 
   ПОКАЗАТЕЛИ НАДЁЖНОСТИ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА
   

Большинство сложных технических систем с длительными сроками службы являются восстанавливаемыми, т.е. возникающие в процессе экс- плуатации отказы систем устраняют при ремонте. Технически исправное

состояние изделий в процессе эксплуатации поддерживают проведением профилактических и восстановительных работ.

Для осуществляемых в процессе эксплуатации изделий работ по поддержанию и восстановлению их работоспособности характерны зна- чительные затраты труда, материальных средств и времени. Как правило, эти затраты за время эксплуатации изделия значительно превышают соот- ветствующие затраты на его изготовление. Совокупность работ по под- держанию и восстановлению работоспособности и ресурса изделий под- разделяют на техническое обслуживание и ремонт, которые, в свою оче- редь, подразделяют на профилактические работы, осуществляемые в плановом порядке, и аварийные, проводимые по мере возникновения от- казов или аварийных ситуаций.

Свойство ремонтопригодности изделий влияет на материальные за- траты и длительность простоев в процессе эксплуатации. Ремонтопригод- ность тесно связана с безотказностью и долговечностью изделий. Так, для изделий с высоким уровнем безотказности, как правило, характерны низ- кие затраты труда и средств на поддержание их работоспособности.

Показатели безотказности и ремонтопригодности изделий являются составными частями комплексных показателей, таких как коэффициенты готовности K_г и технического использования K_{т. и} .

К показателям надёжности, присущим только восстанавливаемым элементам, следует отнести среднюю наработку на отказ, наработку меж- ду отказами, вероятность восстановления, среднее время восстановления, коэффициент готовности и коэффициент технического использования.


m

Средняя наработка на отказ – наработка восстанавливаемого эле- мента, приходящаяся в среднем на один отказ в рассматриваемом интер- вале суммарной наработки или определённой продолжительности экс- плуатации:

T_о  1/ m_t_i,

t 1

где t_i– наработка элемента до i-го отказа; m – число отказов в рассматри- ваемом интервале суммарной наработки.

Наработка между отказами определяется объёмом работы элемен- та от i-гo отказа до (i + 1)-го, где i =1, 2, ..., m.


m

Среднее время восстановления одного отказа в рассматриваемом ин- тервале суммарной наработки или определённой продолжительности экс- плуатации

T_в  1/ m_t_вi,

t1

где t_вi – время восстановления i-го отказа; т – число отказов в рассматри- ваемом интервале суммарной наработки.

Коэффициент готовности K_г представляет собой вероятность того, что изделие будет работоспособно в произвольный момент времени, кро- ме периодов выполнения планового технического обслуживания, когда применение изделия по назначению исключено. Этот показатель является комплексным, так как он количественно характеризует одновременно два показателя: безотказность и ремонтопригодность.

В стационарном (установившемся) режиме эксплуатации и при лю- бом виде закона распределения времени работы между отказами и време- ни восстановления коэффициент готовности определяют по формуле

K_г  T_о / (T_о  T_в ) ,

где Т_о – средняя наработка на отказ; Т_в – среднее время восстановления одного отказа.

Таким образом, анализ формулы показывает, что надёжность изделия является функцией не только безотказности, но и ремонтопригодности. Это означает, что низкая надёжность может быть несколько компенсиро- вана улучшением ремонтопригодности. Чем выше интенсивность восста- новления, тем выше готовность изделия. Если время простоя велико, то готовность будет низкой.

Другой важной характеристикой ремонтопригодности является ко- эффициент технического использования, который представляет собой отношение наработки изделия в единицах времени за некоторый период эксплуатации к сумме этой наработки и времени всех простоев, обуслов- ленных устранением отказов, техническим обслуживанием и ремонтами за этот период. Коэффициент технического использования представляет собой вероятность того, что изделие будет работать в надлежащем режи- ме за время Т. Таким образом, K_т.и определяется двумя основными факто- рами – надёжностью и ремонтопригодностью.

Коэффициент технического использования характеризует долю вре- мени нахождения элемента в работоспособном состоянии относительно рассматриваемой продолжительности эксплуатации. Период эксплуата- ции, для которого определяется коэффициент технического использова- ния, должен содержать все виды технического обслуживания и ремонтов. Коэффициент технического использования учитывает затраты времени на плановые и неплановые ремонты, а также регламенты, и определяется по формуле

K _т.и  t_и / (t_н  t_в  t_р  t_о ) ,

где t_н – время работы; t_н – суммарная наработка изделия в рассматривае- мый промежуток времени; t_в, t_р и t_о – соответственно суммарное время, затраченное на восстановление, ремонт и техническое обслуживание из- делия за тот же период времени, t_и – время работы.

3. 
   ПОКАЗАТЕЛИ НАДЁЖНОСТИ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕЗАВИСИМЫХ ЭЛЕМЕНТОВ
   

Всякая система характеризуется безотказностью и ремонтопригодно- стью. В качестве основной характеристики безотказности системы служит функция надёжности, которая представляет собой вероятность безотказ- ной работы в течение некоторого времени t.

Пусть система состоит из n элементов, функции надёжности которых обозначим через p₁(t), p₂(t), …, p_n(t). Так как элементы, входящие в состав системы, являются независимыми, то вероятность безотказной работы системы определяется как произведение вероятностей составляющих её элементов

P(t)  p₁ (t) p₂ (t)... p_n (t) .

В частном случае, когда функции надёжности составляющих элемен- тов имеют экспоненциальное распределение с постоянными интенсивно- стями отказов, функция надёжности системы определяется по формуле

 ^ 

P(t)  exp[(₁  ₂ ...  _n) t]  exp _ __it_ .

^ i1 ^

Одной из важнейших характеристик безотказности системы является среднее время жизни, которое вычисляют, используя выражение



T_с  _ P(t) DT .

0

Для случая экспоненциального распределения среднее время жизни системы равно

^  ⁿ 

T_с  _exp _ __it_ dt 1/ (₁  ₂  ...  _n) .

₀ ^ i1 ^

Среднее время жизни системы или наработку на отказ по результа- там статистических данных вычисляют по формуле

T_с  T / m ,

где T – суммарная наработка системы, полученная по результатам испы- таний или эксплуатации; т – суммарное число отказов, зафиксированное в процессе испытаний или эксплуатации.

Коэффициент оперативной готовности характеризует надёжность системы, необходимость применения которой возникает в произвольный

момент времени (кроме планируемых периодов, в течение которых приме- нение системы по назначению не предусматривается), начиная с которого система будет работать безотказно в течение заданного времени t.Значение коэффициента оперативной готовности определяют из выражения

K_о  K_г P(t)  P(t)T_c / (T_с  T_в ) .

4. 
   ВЫБОР И ОБОСНОВАНИЕ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ ТЕХНИЧЕСКИХ СИСТЕМ
   

Одной из важнейших задач на этапе проектирования является пра- вильный выбор номенклатуры нормируемых показателей надёжности. Необоснованный выбор показателей надёжности из широкой номенклату- ры имеющихся показателей может привести к неправильным решениям при проектировании системы. Поэтому при выборе показателей надёжно- сти необходимо учитывать назначение системы, условия и режимы её работы, а также её ремонтопригодность.

Информация о назначении системы даёт возможность определить область и интенсивность применения системы по назначению. Сведения об условиях и режимах работы системы используют для оценки влияния факторов окружающей среды на работоспособность проектируемой сис- темы, а также влияния действующих внешних и внутренних нагрузок на несущую способность элементов системы. Количественные значения этих оценок являются исходными данными для расчёта прочности и устойчи- вости элементов и узлов металлоконструкций.

Если по условиям применения систему предполагается ремонтиро- вать в условиях эксплуатации, то в качестве одного из основных показа- телей надёжности следует выбирать коэффициент готовности K_г или ко- эффициент технического использования K_т.и .

В случае если отказ системы или отдельных её элементов приводит к невыполнению важной задачи или нарушает безопасность работы обслу- живающего персонала, а также вызывает угрозу для здоровья и жизни людей, находящихся в зоне действия системы, то для таких систем основ- ным показателем надёжности является безотказность, выражающаяся в виде наработки на отказ или вероятности безотказной работы.

Если в результате простоя системы после отказа возникают большие материальные затраты, то такая система должна иметь хорошую ремонто- пригодность и высокие показатели безотказности.

Если система по условиям эксплуатации подлежит длительному хра- нению (ожиданию работы) или она должна транспортироваться на специ- альных транспортных средствах, то такая система должна обладать высо- кими показателями сохраняемости в соответствующих условиях хранения и транспортирования.


22
Все показатели надёжности проектируемой системы должны обеспе- чивать нормальное её функционирование в течение заданного срока экс- плуатации.