Лекции по ФГП(Физика горных пород). 1. Основные понятия предмета физики горных пород
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
16. Акустические характеристики пород Характер распространения упругих колебаний в горных породах определяется акустическими параметрами пород. К ним относятся скорости распространения упругих волн, коэффициенты поглощения, отражения и преломления и волновое сопротивление. Обычно под скоростью волны понимают скорость распространения некоторой фазы упругих колебаний. Скорость распространения упругих волн в абсолютно упругой изотропной среде определяется по следующим формулам теории упругости: Скорость продольной упругой волны в массиве 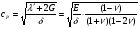 , м/сек, , м/сек,скорость продольной упругой волны в тонкой пластинке породы 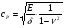 , ,скорость поперечной упругой волны 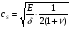 . .Скорость поверхностной волны может быть выражена через скорость поперечной волны 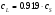 , м/сек или , м/сек или 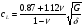 ; ;при этом всегда 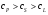 . .Отношение скорости продольных волн к скорости поперечных является функцией только коэффициента Пуассона: 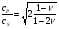 . .Это отношение для изверженных и метаморфических пород обычно изменяется только в пределах от 1,7 до 1,9. Более значительны его колебания в осадочных породах — от 1,5 до 14. Из-за низкого сопротивления сдвигу оно очень велико для глинистых пород, а в рыхлых породах стремится к бесконечности. Таким образом, скорость распространения упругих волн в горных породах определяется их упругими свойствами и плотностью, при этом скорость практически не зависит от частоты колебаний волн. Распространение упругих волн в породах сопровождается постепенным уменьшением их интенсивности по мере удаления от источника излучения из-за поглощения энергии колебаний породой и превращения ее в тепловую и рассеивания акустической энергии на неоднородностях породы. Для однородных тел и монокристаллов поглощение акустических волн определяется вязкостью и теплопроводностью тел. Так же как и для жидкостей, зависимость коэффициента поглощения 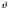 продольной упругой волны от частоты колебаний f квадратичная: продольной упругой волны от частоты колебаний f квадратичная: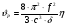 , ,где 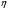 — коэффициент вязкости. — коэффициент вязкости.Зависимость 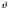 от частоты колебаний для большинства пород не квадратичная, а линейная, например, у каменного угля, каменной соли, сухого песка, гранитов и др. Можно полагать, что поглощение в таких породах обусловлено не столько их вязкостью и теплопроводностью, сколько диффузионным рассеиванием. от частоты колебаний для большинства пород не квадратичная, а линейная, например, у каменного угля, каменной соли, сухого песка, гранитов и др. Можно полагать, что поглощение в таких породах обусловлено не столько их вязкостью и теплопроводностью, сколько диффузионным рассеиванием.В глинистых породах и суглинках 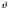 пропорционален пропорционален 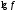 . .Коэффициент поглощения всегда больше в тех породах, в которых скорость упругих колебаний меньше. В расчетах часто используется произведение плотности породы на скорость упругой волны в ней — удельное волновое сопротивление (удельный акустический импеданс) Z, которое представляет собой отношение давления волны σ к мгновенной скорости колебания частиц. Единица удельного волнового сопротивления называется акустическим омом (г/см2·сек). Волновое сопротивление пород определяет их способность отражать и преломлять упругие волны. Отражение и преломление происходит либо на границе между породами с различными акустическими параметрами, либо при переходе упругих волн из внешней среды в породу (и наоборот). 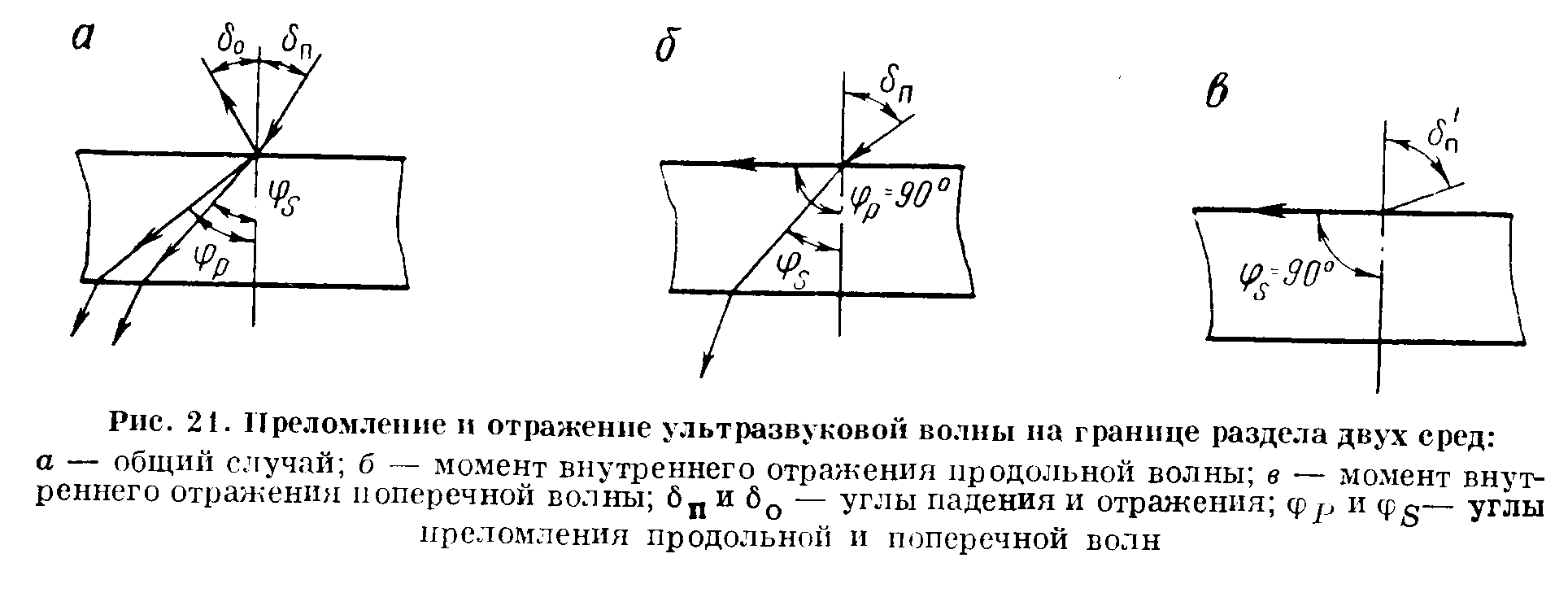 К преломлению и отражению упругих волн в первом приближении можно применить законы геометрической оптики. Коэффициентом отражения энергии Кэназывается отношение энергии отраженной волны WRк энергии падающей волны W0 . При этом углы падения δп и отражения δ0 звуковой волны от границы раздела равны (рис. 21). При переходе из среды с малым волновым сопротивлением в среду с большим сопротивлением основная часть звуковой энергии отражается. Так, при переходе упругих колебаний из воздуха в воду отражается 99,8% их энергии, а при переходе из воды в породу — около 85%. Ввиду того, что скорости волн разных типов различны, в результате прохождения ультразвукового луча в породе происходит разделение волны по направлениям на: продольные и поперечные. Если ультразвуковой луч падает на границу раздела перпендикулярно, происходит только отражение. При угле падения δп > 0° происходит как отражение, так и преломление упругой волны. Постепенным увеличением угла δп можно добиться такого момента, когда произойдет полное внутреннее отражение (угол преломления φ = 90°) сначала продольной (первый критический угол δп) затем поперечной волны (второй критический угол δп , рис. 21). Если звуковая волна отражается от границы поверхности, то в волновом поле перед этой поверхностью происходит наложение падающей волны на отраженную — интерференция. При этом решающее значение имеет угол падения волны и сдвиг фазы между падающей и отраженной волнами. Сдвиг фазы определяется волновым сопротивлением отражающей среды. При совпадении отраженной и падающей волн по фазе происходит их суммирование и амплитуда суммарной волны значительно возрастает — появляются стоячие волны. Это явление находит широкое использование в практике. 17. Действие упругих колебаний на горные породы Упругие колебания низкой частоты достаточной мощности чаще всего приводят к тем же последствиям, что и механическое напряжение. При этом происходит усталостное разрушение пород. Возможен эффект уплотнения и сортировки рыхлых горных пород. Особые явления наблюдаются при распространении в горных породах и жидкостях высокочастотных упругих колебаний (в том числе и ультразвука). Малая длина волн позволяет их концентрировать в узкий пучок. Это способствует получению высоких интенсивностей звука с предельными амплитудами смещения и соответствующему проявлению механических, тепловых, электрических и химических эффектов. Причиной этих эффектов являются вызванные ультразвуком колебания частиц, особенно продольные колебания, связанные с деформациями сжатия и растяжения. При прохождении ультразвука через жидкость возникает кавитация. Когда в некоторых участках жидкости внутреннее давление р будет ниже статического ее давления р0, происходит разрыв жидкости. Жидкость испаряется и образуются кавитационные пузырьки, которые захлопываются сразу же, как только р станет больше р0. Появлению кавитации особенно способствует наличие в жидкости инородных тел или пузырьков, являющихся как бы центрами ее возникновения. Вблизи этих центров силы притяжения между молекулами воды значительно ослаблены. Кавитацию можно вызвать различными способами — механическим (гидравлические удары, ультразвук), электрическим (элек трический разряд в жидкости) и др. Ультразвуковые волны создают в жидкости зоны растяжения и зоны сжатия. Кавитационные пузырьки появляются в зонах растяжения. Кавитация вызывает эрозию поверхности твердых тел, находящихся в жидкости. При частотах более 5 Мгц кавитация не наблюдается (процесс возникновения, и исчезновения пузырьков не успевает завершиться). Кавитация в жидкости является причиной возникновения некоторых эффектов, важнейшим из которых следует считать диспергацию (разрушение) твердых тел, расположенных в области распространения звука. Скорость ультразвукового разрушения определяется, прежде всего, хрупкостью твердых тел. Чем больше хрупкость, тем при прочих равных условиях выше скорость разрушения. Поэтому легко диспергируются ультразвуком такие породы, как гипс, слюда, графит и сера. Эффект диспергирования усиливается при добавке к воде поверхностно-активных веществ в количестве менее 0,2%. Кавитация вызывает также дегазацию жидкостей и расплавов. Дегазация связана с понижением давления жидкости при растяжении и выделением вследствие этого газа. Кавитация вызывает возникновение электрических и химических эффектов ультразвука. Из электрических эффектов основным является люминесценция жидкости. Химические эффекты ультразвука вызывают ускорение реакции, окисление, восстановление и конденсацию. Из механических эффектов в жидкостях и газах следует отметить явление, обратное диспергации, — коагуляцию (осаждение) взвешенных в воздухе, газах или жидкостях твердых частиц. Ультразвук, проходя через жидкость, в которой взвешены частицы породы, заставляет их совершать колебания, частота и амплитуда которых зависят от массы частиц. Это приводит к увеличению частоты соударений частиц, их слипанию, укрупнению и осаждению. Упругие колебания звуковой и инфразвуковой частоты способны вызвать тиксотропию (разжижение) влажных глинистых пород. Колебания также снижают внутреннее трение рыхлых скальных пород, так как в результате вибрации связь между частицами становится менее устойчивой. 18 ТЕОРИИ ПРОЧНОСТИ ТВЕРДЫХ ТЕЛ Теоретическая прочность идеального кристалла Теоретической прочностью материала называется механическое напряжение, необходимое для разрушения идеального кристалла, не содержащего дефектов, по определенной кристаллографической плоскости. Для вычисления теоретической прочности воспользуемся феноменологическим подходом, используя известные экспериментальные данные об энергетических затратах при разрушении тела, а также при его деформировании под действием механических напряжений. Первое уравнение учитывает экспериментально известную энергию активации Uа, соответствующую энергетическим затратам, необходимым для разделения тела на две части. Вычисляется как отношение затраченной на разрушение энергии к площади образованных поверхностей. Энергия активации Uа и удельная энергия разрушения γ связаны равенством Uа=2 γ (Дж/м2). Второе уравнение описывает линейный закон взаимосвязи между действующим напряжением и относительной деформацией. В соответствии с законом Гука имеем 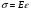 где 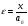 ( х - величина смещения относительно положения равновесия, а0 - расстояние между молекулами в положении равновесия). ( х - величина смещения относительно положения равновесия, а0 - расстояние между молекулами в положении равновесия).На рис. стр.25 представлены качественная форма энергетической кривой и диаграмма напряжение – деформация твердого тела. На начальном участке деформирования выполняется закон Гука, а на участке перед разрушением кривая выполаживается, отражая пластическое деформирование материала. Кривая s(e) может быть аппроксимирована синусоидой, отражающей особенности начального и конечного участков деформирования 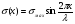 где 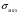 - максимальное разрушающее напряжение, l - параметр аппроксимации. - максимальное разрушающее напряжение, l - параметр аппроксимации.Для начального участка синусоиды выполняется приближенное равенство 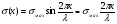 Можно приравнять следующие выражения 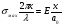 , ,Откуда следует выражение параметра аппроксимации 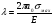 . .Потенциальная энергия деформации П соответствует площади, ограниченной кривой 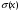 на участке перед разрушением и осью абсцисс на участке перед разрушением и осью абсцисс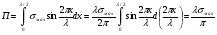 . .В соответствии с законом сохранения энергии запишем равенство между предельной величиной потенциальной энергии деформации П и энергией активации Uа 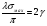 . .Воспользовавшись выражением для l получим искомую формулу для расчета теоретической прочности идеального кристалла (формула Орована) 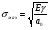 Видно, что теоретическая прочность возрастает с увеличением модуля Юнга Е и удельной поверхностной энергии разрушения g. С увеличением расстояния а0 между молекулами кристалла его прочность уменьшается. Расстояние а0 обратно пропорционально плотности твердого тела, т.е. 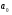 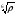 . .Более плотные материалы отличаются большей плотностью. Такая корреляция между прочностью и плотностью действительно имеет место при анализе свойств различных горных пород. Прочность тела определяется величиной напряжений, при которых происходит его разрушение. Критические значения разрушающих напряжений зависят не только от свойств твердого тела, но и от характера самих напряжений. В связи с этим различают пределы прочности пород на сжатие σсж, растяжение σр, сдвиг τсдв, изгиб σизг и т. д. При воздействии на твердое тело одноосных нагрузок соответствующие им пределы прочности полностью характеризуют способность тела выдерживать нагрузки. В случае сложнонапряженного состояния необходимо выделить дополнительные критерии. Галилеем была предложена теория нормальных напряжений (первая теория прочности), по которой разрушение материала наступает тогда, когда наибольшее нормальное напряжение σмах дости гает некоторого предельного значения σ0 (предела прочности на одноосное сжатие σсж или на одноосное растяжение σр ): 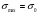 . .Экспериментальные данные не подтверждают этой теории. Например, при деформациях, в которых развиваются большие касательные напряжения (сдвиг, кручение), разрушение происходит при нормальных напряжениях, значительно меньших, чем предельные сжимающие, а в случае всестороннего сжатия — при больших, чем предельные, напряжениях. Сен-Венаном была сформулирована теория максимальных деформаций (вторая теория прочности), согласно которой разрушение материала произойдет тогда, когда наибольшие относительные деформации станут равными их предельному значению при простом сжатии. Эта теория не учитывает роли касательных и других напряжений в процессах разрушения. В теории максимальных касательных напряжений, предложенной Кулоном, в качестве критерия разрушаемости материалов выдвигаются максимальные касательные напряжения 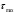 , при которых разрушается порода: , при которых разрушается порода: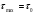 . .Максимальные касательные напряжения при сложном напряженном состоянии равны 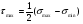 , ,где 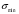 - минимальные нормальные напряжения, поэтому условие разрушения согласно этой теории будет - минимальные нормальные напряжения, поэтому условие разрушения согласно этой теории будет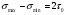 . .Эта теория подтверждается экспериментальными данными для материалов, разрушение которых происходит в зоне пластического течения. К. Максвелл предложил положить в основу теории прочности энергетический принцип — величину работы по изменению формы образца при его деформировании без изменения объема. Условие разрушения в этом случае выражается через нормальные напряжения: 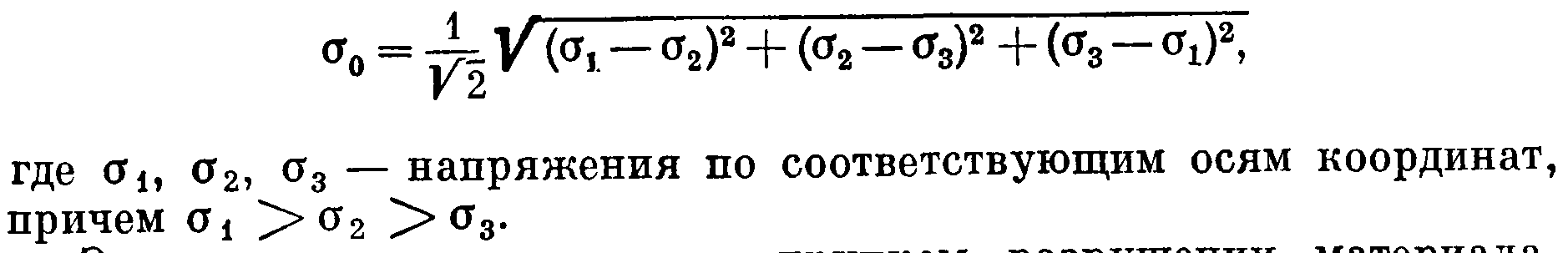 Эта теория приемлема при хрупком разрушении материала. Для горных пород наиболее широко используют теорию прочности Мора, основанную на зависимости между касательными и нормальными напряжениями в каждой точке тела, находящегося в сложно напряженном состоянии. В системе координат (σ — τ) эта зависимость выражается кривой, огибающей семейство кругов напряжений, построенных для различных случаев предельного напряженного состояния (σсж, σр, τсдв) испытываемого образца (рис. 25). Кривая характеризует предельно напряженное состояние твердого тела в момент его разрушения. Огибающую кругов Мора часто называют паспортом прочности горных пород. Согласно теории Мора разрушение наступит тогда, когда либо касательные напряжения превысят величину, ограниченную огибающей, либо нормальные растягивающие напряжения превысят определенный предел при τ = 0. Теория Мора согласуется с экспериментами, проводимыми на образцах горных пород. Наиболее просто аналитическая зависимость предельных каса тельных напряжений τ от нормальных σн изображается прямой линией (см. рис. 25): 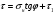 где φ — угол наклона прямоугольного отрезка огибающей к оси абсцисс; τ1 (С) — предельное касательное напряжение в породе при отсутствии нормального напряжения (сцепление). Угол φ называется углом внутреннего трения, а 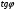 — коэффициентом внутреннего трения (коэффициентом пропорциональности между приращениями нормальных и касательных напряжений при разрушении породы). — коэффициентом внутреннего трения (коэффициентом пропорциональности между приращениями нормальных и касательных напряжений при разрушении породы).Показатель τ1 (С) называется сцеплением горной породы и количественно равен пределу прочности породы на срез при отсутствии нормальных напряжений. Для рыхлых пород группы по строению З.п, не обладающих пределом прочности на растяжение и силами сцепления, диаграмма Мора имеет вид прямой, исходящей из начала координат (см. рис. 25). 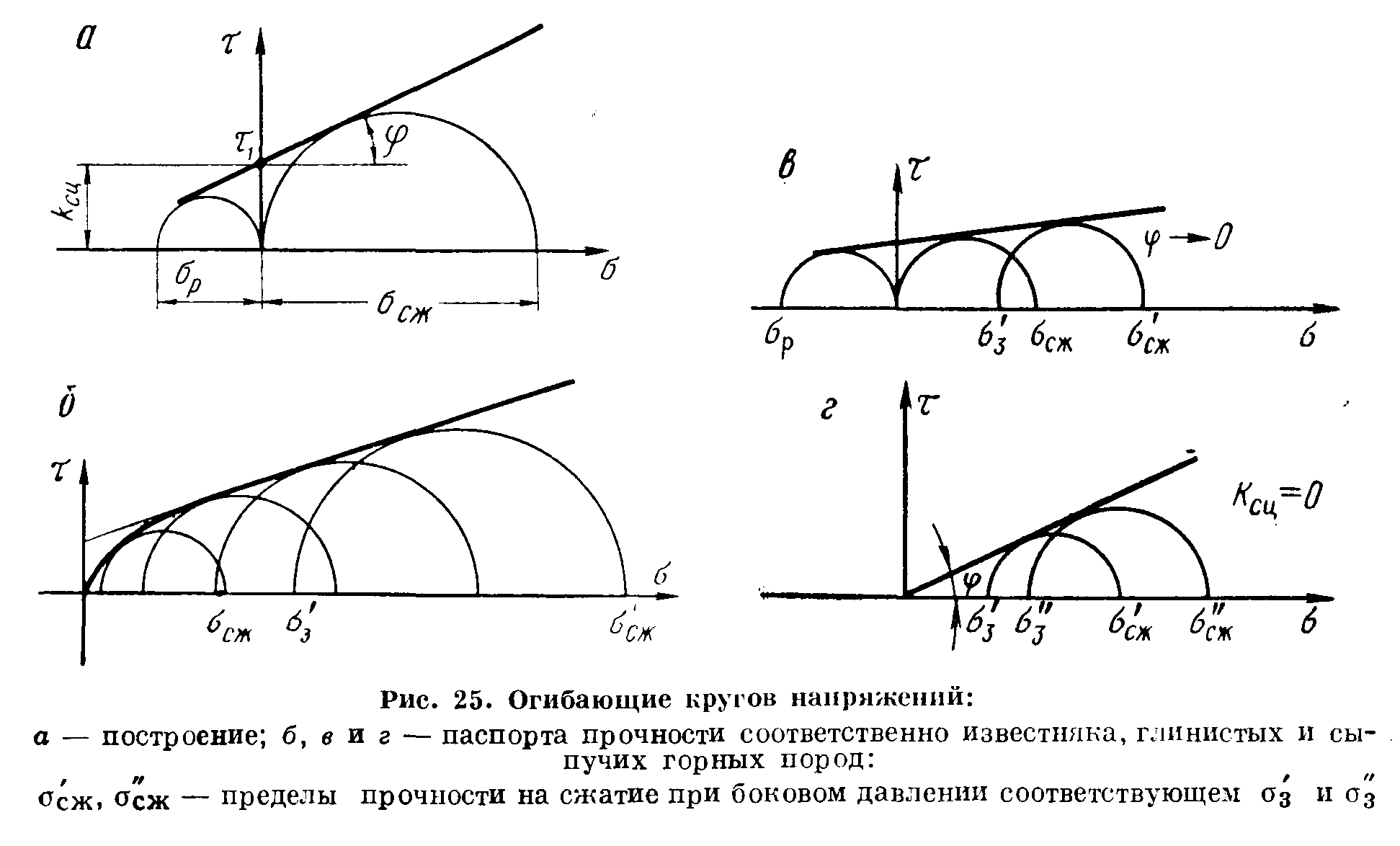 При этом 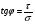 — характеризует угол естественного откоса рыхлых массивов. — характеризует угол естественного откоса рыхлых массивов.Для связных пластичных пород (σсж ≈ σр) огибающая кругов Мора близка к линии, параллельной оси абсцисс (см. рис. 25). Огибающая кругов напряжений для скальных пород изображается в виде параболы второго порядка (см. рис. 25) |

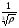 ,
,