Лекции по ФГП(Физика горных пород). 1. Основные понятия предмета физики горных пород
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
Термонапряжения возникают в результате превращения тепловой энергии в механическую. Воздействие термонапряжений на изменение свойств пород аналогично воздействию механических напряжений. Термохимические и физические превращения в горных породах при нагреве могут быть следующими: 1) переход породы из одного агрегатного состояния в другой — плавление — отвердевание; испарение — сжижение; возгонка16. Плавление породы характеризуется ее температурой и теплотой плавления. Теплота плавления — это количество тепла, необходимого для расплавления единицы массы породы при постоянных температурах и давлении; 2) переход минералов из одной кристаллической формы в другую без изменения их химического состава — полиморфные превращения. Полиморфные превращения пород сопровождаются скачкообразными изменениями некоторых их свойств. Полиморфные превращения присущи многим минералам. Наиболее широко известны полиморфные превращения кварца при повышенных температурах, сопровождающиеся значительным увеличениемего объема (переход β-кварца в α-кварц при Т = 573°С); 3) дегидратация — удаление химически связанной воды из минералов и горных пород; 4) диссоциация — разрушение минерала с выделением газообразной фазы; 5) окислительно - восстановительные процессы, присущи как правило, медно-никелевым и свинцово-цинковым сульфидным рудам и каменным углям. Это явление приводит к самовозгоранию руд и углей в процессе их добывания и хранения. Критической температурой, при которой происходит быстрый переход к самовозгоранию, для бурых углей является температура 40 — 60°С, для жирных каменных углей — 60—70°С, для антрацитов — 80°С, для сульфидных руд — 40—60°С. Под воздействием низких температур также происходит изменение внутреннего строения пород и сил связей между отдельными частицами. Таким образом, тепловое воздействие приводит к изменению свойств пород в различных направлениях. 12. Напряжения и деформации в горных породах Под воздействием внешних сил тело изменяет форму и объем, в результате этого в нем возникают внутренние силы, стремящиеся к восстановлению прежней формы. Поверхностная плотность силы, возникающей в каждом элементе тела, называется напряжением. Напряжение σ — величина векторная. Она зависит от внутренних свойств породы (сил и характера связей между частицами), формы образца и от действия внешних сил. Силы, действующие в одном направлении, вызывают в образце линейное напряженное состояние, действующие в двух направлениях, но в одной плоскости — плоское напряженное состояние, а в остальных случаях — объемное напряженное состояние. В абсолютно плотной породе напряжения рассчитываются по формуле: 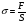 , ,где S — площадь, на которую воздействует сила. В пористых породах 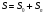 , ,где S0 — площадь контакта минеральных зерен; Sп — площадь, занятая порами. Напряжения концентрируются только в области контакта минеральных зерен 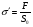 Поэтому с увеличением пористости, трещиноватости и выветрелости, при прочих равных условиях, напряжения в породе возрастают. Степень возрастания истинных напряжений в пористой породе оказывается еще больше из-за местной концентрации напряжений, возникающей в углах трещин и пор. Рассмотрим тело произвольной формы, находящееся в равновесии под действием приложенных к нему внешних сил. Рассечем мысленно рассматриваемое тело какой-либо поверхностью на две части. Заменим действие одной части приложенной к сечению внутренними силами, так чтобы оставшаяся часть находилась в равновесии. Вообще говоря, внутренние силы неравномерно распределены по площади сечения. Выделим на сечении элементарную площадку 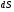 на которую действует сила на которую действует сила 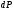 . .В этом случае отношение 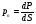 называется вектором напряжения на площадке 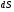 . .Рассекая рассматриваемое тело плоскостями параллельными прямоуголной системе координат, можно прийти к элементарному кубику на каждую внешнюю грань которого действуют свой вектор напряжений. Проекции этих векторов на оси координат представляют девять компонентов напряжений — два касательных и одно нормальное на каждой грани кубика (рис. 10). Все они представляют одну физическую величину, называемую тензором напряжений. 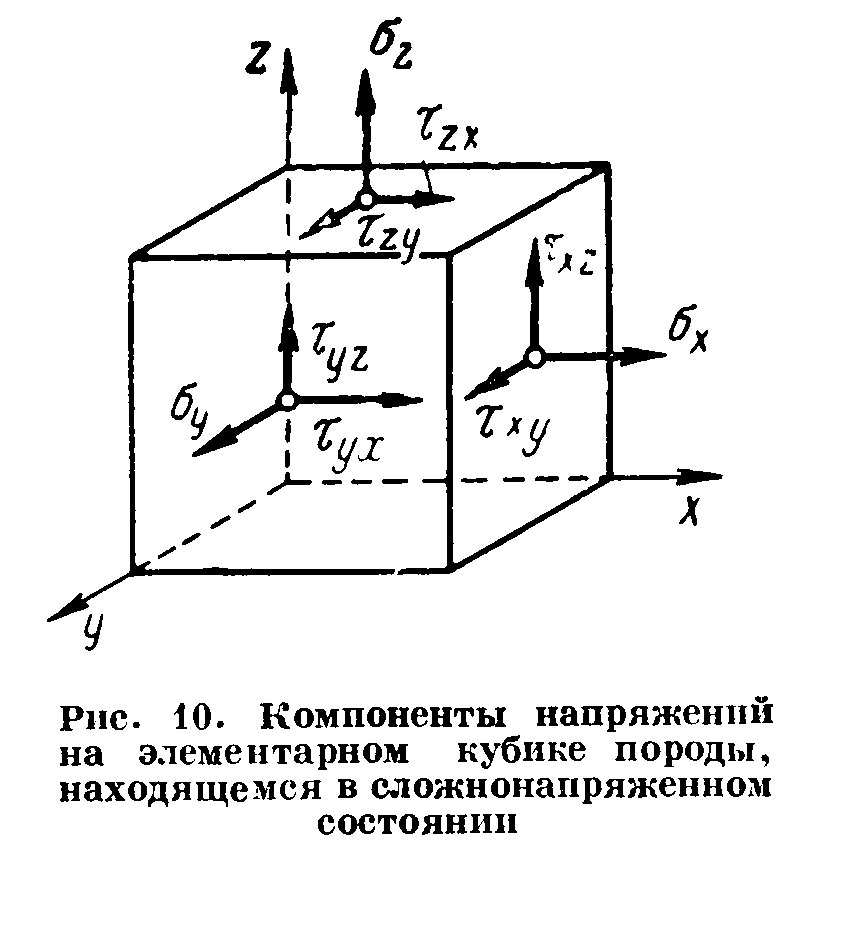 Запись тензора напряжений имеет следующий вид 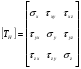 Сумма моментов относительно любого ребра рассматриваемого элементарного кубика должна быть равна нулю. Отсюда следует закон парности касательных напряжений: 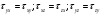 . .Таким образом, напряженное состояние твердого тела в любой плоскости можно охарактеризовать действующими в нем нормальными и касательными напряжениями. Они взаимосвязаны и могут быть рассчитаны методом сложения векторов. На рис.11 приведен пример нагружения образца осевым (  ) и боковым ( ) и боковым ( ) усилиями ( ) усилиями (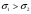 ). Для отыскания нормального ( ). Для отыскания нормального (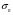 ) и касательного ( ) и касательного ( ) напряжения, действующего на наклонной площадке, расположенной под углом ) напряжения, действующего на наклонной площадке, расположенной под углом 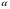 , можно воспользоваться графическим методом с помощью кругов напряжений Мора, которые строятся следующим образом (рис. 11): на оси абсцисс откладывают максимальное и минимальное значения нормальных напряжений, действующих на образец; на разности отрезков, как на диаметре, строится полуокружность. , можно воспользоваться графическим методом с помощью кругов напряжений Мора, которые строятся следующим образом (рис. 11): на оси абсцисс откладывают максимальное и минимальное значения нормальных напряжений, действующих на образец; на разности отрезков, как на диаметре, строится полуокружность.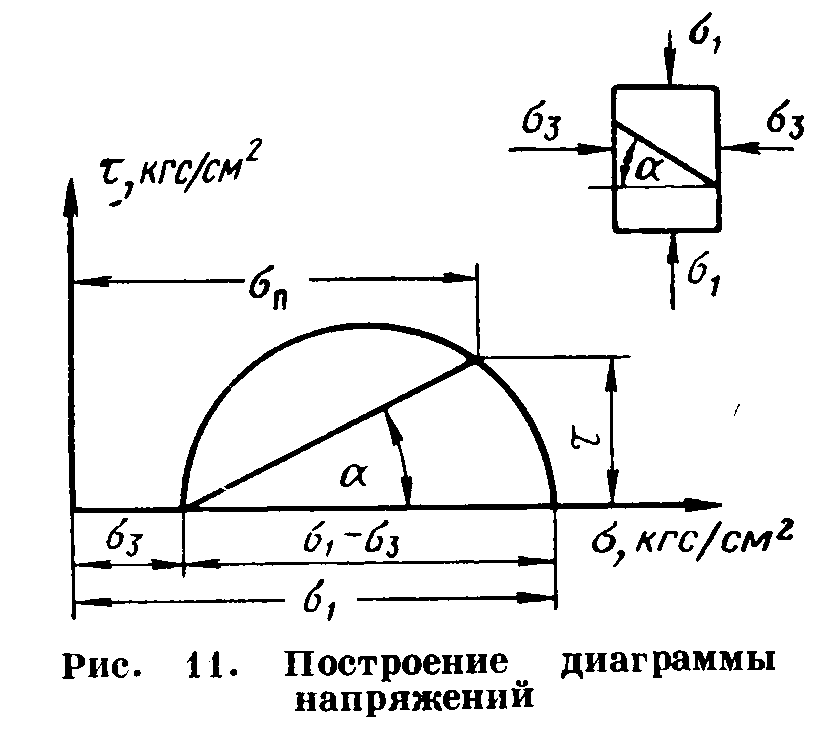 Значения касательного и нормального напряжений в любой точке образца могут быть определены, если задан угол наклона плоскости, в которой определяются напряжения. Под этим углом из точки пересечения круга с абсциссой проводят прямую до пересечения с полуокружностью. Координаты точки пересечения полуокружности с прямой численно равны значениям определенных напряжений. Каждому частному значению напряженного состояния соответствует свой круг напряжений. Напряжения в породах могут возникать под воздействием не только внешних сил, но и различных физических полей. Напряжения бывают термические, усадочные, обусловленные неравномерным охлаждением объема, остаточные, возникающие в результате неравномерного распределения напряжений из-за местной текучести материала, и др. На эти напряжения накладываются напряжения от внешнего воздействия, которые могут либо увеличивать, либо уменьшать их. Под воздействием внешних сил горная порода испытывает изменения линейных размеров, объема или формы, которые называются деформациями. Деформации, соответствующие нормальным напряжениям, выражаются через относительное изменение и линейных размеров образца 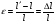 Гдеl' и l— длина образца соответственно в деформированном и недеформированном состоянии. Относительные деформации, соответствующие касательным напряжениям, выражаются через тангенс угола сдвига 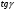 граней элементарного объема образца. Ввиду малости угла граней элементарного объема образца. Ввиду малости угла 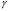 справедливо соотношение справедливо соотношение 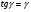 . .Деформации удлинения и сдвига можно разложить на составляющие по осям координат. В теории упругости, (раздел теория деформаций) дается вывод тензора деформаций, определяющий состояние деформации в любой точке тела: 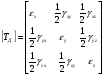 13. Понятие о диаграмме деформирования Если при деформировании (нагружении) образца горной породы производится одновременное измерение напряжений (деформаций), то можно построить график. 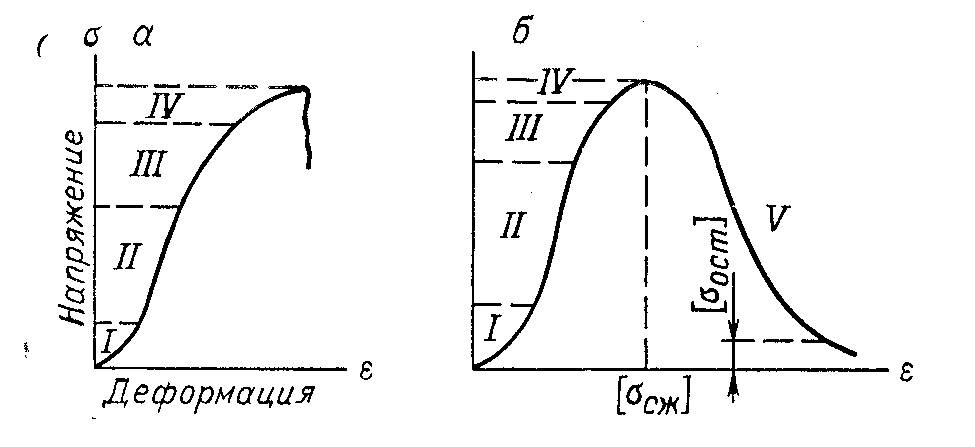 Рис. 6.7 Типичные кривые "напряжение-деформация" для горных пород, получаемые на обычных испытательных прессах (а) и машинах с повышенной жесткостью (б). l-V - области: I - закрытия структурных дефектов, II - линейного деформирования, III - образования микротрещиноватости, IV - разветвления и слияния трещин, V - снижения грузонесущей способности. Этот график в координатах «относительная продольная деформация – осевое продольное напряжение» называется диаграммой деформирования. Максимальная несущая способность образца называется пределом прочности, а соответствующая ей деформация называется разрушающей. Разрушающая деформация условно делит процесс деформирования на две стадии – стадия допредельного деформирования и стадия запредельного деформирования (стадия разупрочнения). Если испытания проводятся на жестком относительно образца оборудовании, то получаем полную диаграмму деформирования с допредельным запредельным участками. Если испытания проводят на мягком относительно образца оборудовании, то получают допредельный участок нагружения, т.к. после пика диаграммы, выполняется условие хрупкого разрушения и происходит динамическое разрушение образца, сопровождающееся разлетом его частей. На допредельной стадии принято выделять линейный (упругий) участок – определяющий его параметр условно называется модулем упругой деформации; точку перехода с линейного на нелинейный участок – предел упругости и соответствующей ему деформации на пределе упругости; при интегральной оценке всего допредельного участка деформирования выделяют секущий модуль деформации, проходящий через точку предела прочности. На запредельной стадии деформирования выделяют предел остаточной прочности, соответствующий выходу на остаточную ветвь диаграммы деформирования и соответствующая ему деформация остаточной прочности. Также выделяют секущий модуль спада, проходящий через предел прочности и предел остаточной прочности и касательный модуль спада – за него часто принимают т.н. модуль хрупкости – касательная на наиболее крутом участке запредельной стадии деформирования. Часто диаграмму деформирования строят со стадией разгрузки. По этой стадии определяют модуль упругости (модуль Юнга). Для многих горных пород модуль упругости определенный на различных участках диаграммы имеет достаточно близкие значения. В этой связи, при испытаниях, разгрузку можно делать на любом участке диаграммы. Деформации могут быть неразрушающими и разрушающими. Разрушающие деформации приводят к разделению породы на отдельные части; неразрушающие — изменяют размеры, форму и объем породы без нарушения ее сплошности. Неразрушающие деформации бывают упругие и пластические. При упругих связях наблюдается прямая пропорциональность между напряжениями и соответствующими деформациями. С ростом величины упругой деформации в образце накапливается потенциальная энергия, которая после снятия нагрузки возвращает образец в исходное состояние. Характерной чертой пластических деформаций является их необратимость после снятия нагрузки — форма и размеры образца полностью не восстанавливаются. При достижении определенной величины нагрузки возможно возрастание деформации даже при постоянной или уменьшающейся нагрузке. Пластические деформации происходят длительное время. Один вид деформации может переходить в другой при возрастании напряжений или увеличении времени их воздействия. Так, при увеличении напряжений можно наблюдать три области деформации породы: упругую, пластическую и разрушающую. При длительном воздействии на породу какого-либо постоянного напряжения также можно выделить на диаграмме деформирования три вида деформации (рис. 12). На рисунке приведены допредельные участки диаграммы деформирования, полученные при испытании на мягком оборудовании. В зависимости от соотношения вида деформаций горные породы подразделяются на упругие или хрупкие (пластическая зона практически не наблюдается), упруго-пластичные (разрушающей деформации предшествует зона пластической деформации) и пластичные (упругая деформация незначительна). 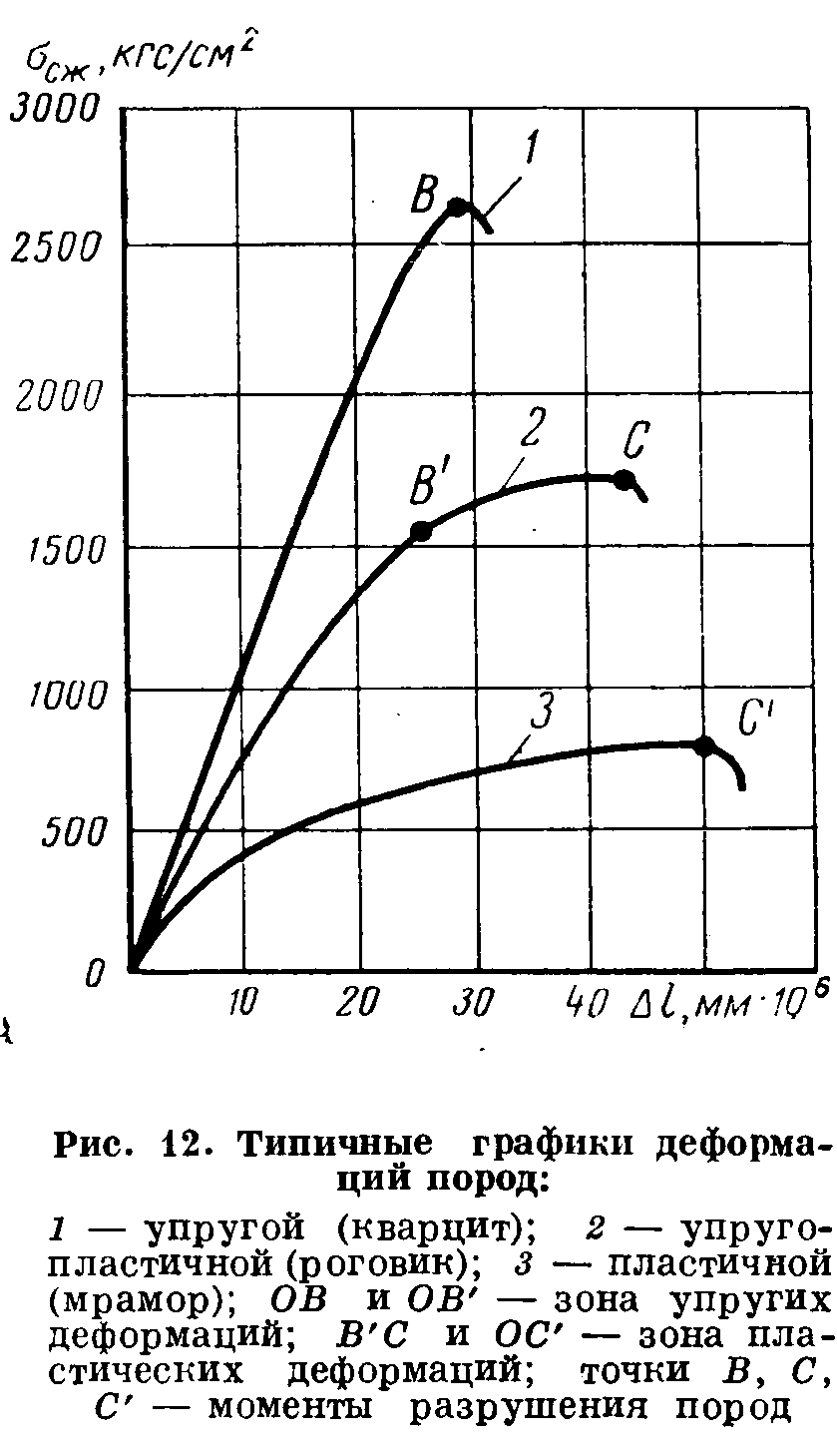 Деформации в горных породах определяются характером внутренних связей между частицами породы; любые внешние поля, воздействующие на связи между частицами породы, изменяют величину и вид деформации в ней. Приведем полную диаграмму деформирования образца горной породы полученную в условиях одноосного сжатия на жестком испытательном оборудовании, а также стандартные параметры деформирования, определяемые при испытаниях. 14. Упругие свойства горных пород Для каждого вида приложенных напряжений существует свой коэффициент пропорциональности между напряжениями и упругими деформациями; он является параметром породы, оценивающим ее упругие свойства. Коэффициент пропорциональности между нормальным напряжением (сжимающим или растягивающим) и соответствующей ему относительной продольной деформацией и называется модулем упругости (модулем Юнга) Е: 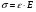 . .Коэффициент пропорциональности между касательным напряжением  и соответствующей деформацией сдвига и соответствующей деформацией сдвига 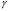 носит название модуля сдвига G: носит название модуля сдвига G: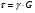 Модуль упругости Е и модуль сдвига Gсчитаются основными упругими характеристиками породы. Пользуются и другими упругими параметрами пород. В случае объемного напряженного состояния породы связь между напряжением 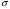 и относительным изменением объема и относительным изменением объема 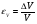 выражается через модуль всестороннего сжатия выражается через модуль всестороннего сжатия 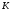 : :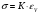 где 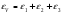 ( (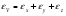 ). ).Для рыхлых пород пользуются понятием модуля одностороннего сжатия М— коэффициентом пропорциональности между продольным напряжением и соответствующей ему деформацией при расположении пробы в цилиндре с жесткими стенками. Широко применяют также еще один упругий параметр — коэффициент Пуассона  , являющийся коэффициентом пропорциональности только между деформациями — относительными продольными , являющийся коэффициентом пропорциональности только между деформациями — относительными продольными 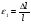 и относительными поперечными и относительными поперечными 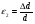  Коэффициент Пуассона — величина безразмерная. Он связан с величинами Е и Gуравнением 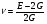 Для изотропных тел достаточно знать лишь два упругих параметра, другие параметры могут быть вычислены по соотношениям теории упругости. Чаще всего в качестве основных параметров экспериментально определяют и используют в расчетах модуль упругости и коэффициент Пуассона. Если образец породы испытывает объемное напряженное состояние, необходимо учитывать деформации и напряжения во всех направлениях. Такое состояние образца породы может выражаться обобщенным законом Гука Аналогично может быть описано состояние породы, если на все ее плоскости действуют касательные напряжения. Модули упругости характеризуют жесткость пород, их способность сопротивляться внешним воздействиям. Величина, обратная модулю упругости, называется коэффициентом соответствующей деформируемости (податливости). Породы, обладающие большими значениями модуля упругости, как правило, имеют малую зону пластических деформаций, т. е. происходит хрупкое разрушение пород. Поэтому энергия разрушения W породы с большим значением Е часто меньше энергии разрушения породы с небольшим значением Е и высокой пластичностью. 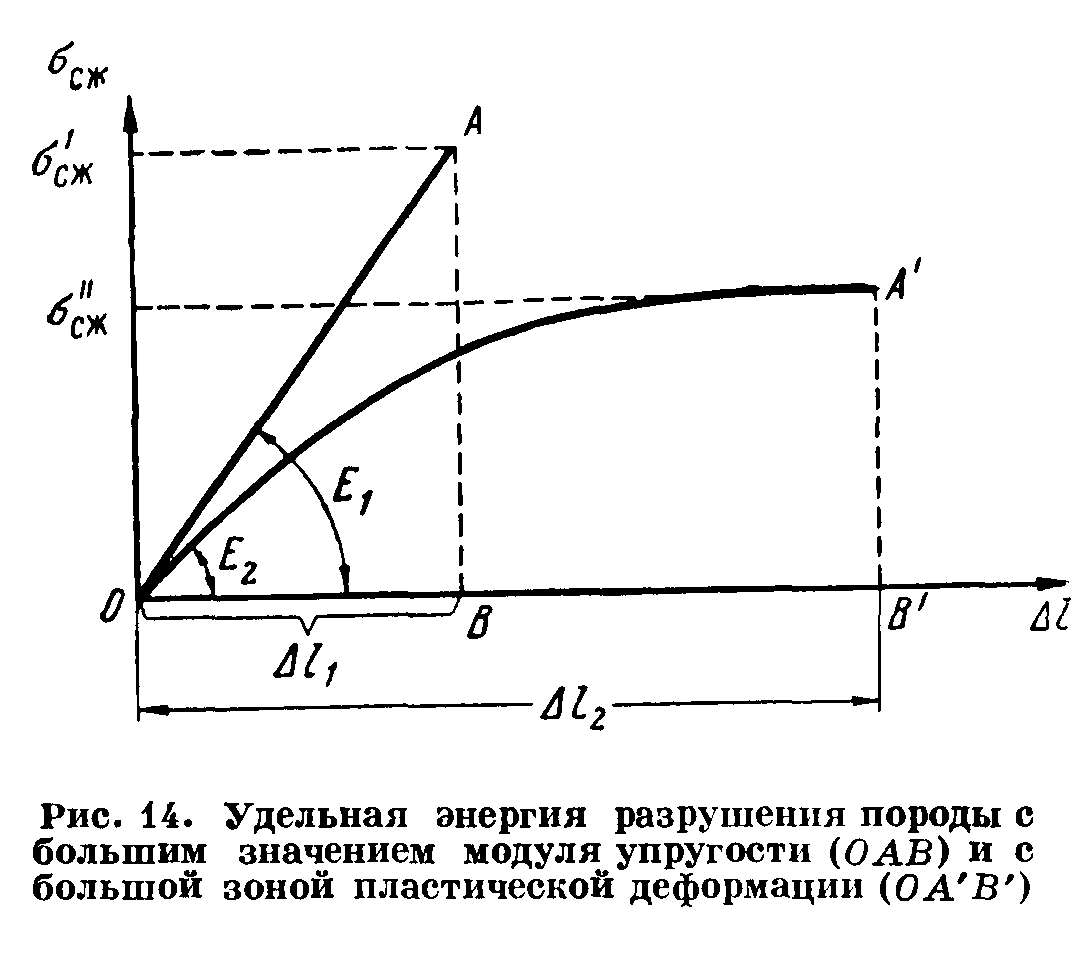 Удельная энергия упругой деформации или хрупкого разрушения равна (рис. 14): 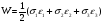 . .В зависимости от целей использования упругих параметров их определяют статическим или динамическим способом. Статические свойства характеризуют породу при довольно длительных процессах воздействия на нее нагрузки, в то время как динамические свойства характеризуют ее при мгновенных воздействиях (взрывание, ударное бурение и т. п.). 15. Распространение упругих колебаний в породах Если к участку породы ограниченных размеров мгновенно приложить нагрузку (удар), вызывающую напряжения, которые не превышают предел упругости, то этот участок будет испытывать деформацию, т. е. смещение частиц по направлению действующей силы. Ввиду того, что частицы породы жестко связаны между собой, деформация одной частицы вызывает смещение других, более удаленных частиц. Происходит распространение упругой деформации с определенной скоростью. При отсутствии потерь энергии за счет трения соседних частиц упругое возмущение должно распространяться по всей породе. Произведение массы т элементарного объема на его ускорение, согласно второму закону Ньютона, равно сумме всех сил 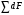 , действующих на этот объем: , действующих на этот объем:Сумму всех сил вдоль любой оси координат можно выразить как сумму всех элементарных напряжений, умноженных на соответствующую площадь, на которую они действуют. Упругие колебания - это процесс распространения в породе знакопеременных упругих деформаций ее частиц; частота этих колебаний может быть самой различной в зависимости от частоты генератора, возбуждающего их. По частоте колебаний упругие волны подразделяются на инфразвуковые – частота колебаний до 20 гц, звуковые – 20 - 20 000 гц, ультразвуковые – более 20000 гц, гиперзвуковые — более 1010 гц. Частота гиперзвуковых колебаний приближается к частоте тепловых колебаний молекул (1013 гц). Волны низкой частоты, быстро затухающие и распространяющиеся в земной коре, но сят название сейсмических. Упругие волны возникают в результате распространения деформаций в веществе. В зависимости от вида деформаций могут возникать волны различных типов (рис. 20).  Деформации попеременного объемного сжатия и растяжения обуславливают распространение в веществе продольных упругих колебаний. Продольные упругие волны распространяются в любой среде — газах, жидкостях и твердых телах, так как все вещества обладают сопротивлением объемному сжатию. Продольные упругие волны вызывают звуковые явления. Волны второго типа, обусловленные распространением попеременных деформаций сдвига в среде, называются поперечными. Поперечные волны характерны только для твердых тел, ибо сопротивление сдвигу в жидкостях и газах отсутствует. Эти два типа волн распространяются по всему объему породы и поэтому называются объемными. Поскольку продольные волны являются наиболее быстрыми (обладают наибольшей фазовой скоростью) и приходят из точки излучения в точку приема первыми, то их принято обозначать буквой P (от слова prima - первый). Поперечные волны приходят в точку приема вторыми, так как их фазовая скорость меньше, чем у продольных. Эти волны принято обозначать буквой S (от слова secunda - второй). Частицы тела, в частности горной породы, находящиеся на поверхности, испытывают особое состояние, так как встречают меньшее сопротивление своим перемещением в сторону свободной поверхности. В результате этого на поверхности возникает плоская поверхностная (рэлеевская) волна, которая характеризуется движением частиц, образующим траекторию в виде эллипса с большой осью, направленной перпендикулярно перемещению волны. В этом случае каждая частица породы совершает двойное колебание: вдоль и поперек направления движения волны. Для образцов пород типа стержней различают также крутильные и изгибные волны. |
