Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР. 1 отображение просранства пользователя и машинного носителя 4
 Скачать 1.86 Mb. Скачать 1.86 Mb.
|
4.3 Заливка с затравкой.При данном способе заливки тем или иным способом выбирается произвольная точка, являющаяся заведомо внутренней для заданной области. Эта точка закрашивается. Закрашиваются также все ее не закрашенные соседи по заданному критерию связности и их адреса записываются в стек. Далее из стека извлекается адрес очередной точки и с ней поступают точно так же, как с предыдущей. Процедура повторяется до тех пор, пока в стеке будет находиться адрес хотя бы одной точки. При реализации рассматриваемого способа возможно использование или восьмисвязного, или четырехсвязного соседства, которые поясняются ниже приведенным рисунком (). 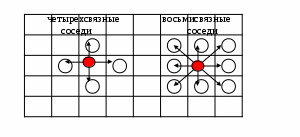 Рис. Заливка с затравкой.‑38 Процесс закраски области данном способом иллюстрируется на ниже приведенном рисунке (Рис. Заливка с затравкой.-39). На рисунке приведена траектория обработки точек с указанием адресов стека, в которые помещаются их координаты. Закрашенная точка соответствует точке-затравке. 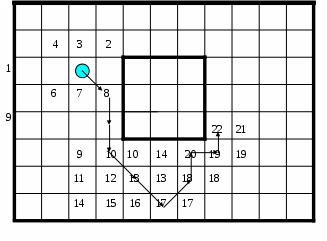 Рис. Заливка с затравкой.‑39 На приведенном рисунке используется восьмисвязное соседство, и просмотр соседей выполняется в направлении против часовой стрелке, начиная с левого. В начальном состоянии стек пуст. Способ сравнительно прост, однако его реализация, как травило, требует большой емкости стека. Для уменьшения требуемого объема памяти для организации стека используется модификация этого способа, которая называется «заливка с затравкой с запоминанием соседних групп». При использовании способа заливки с затравкой с запоминанием соседних групп используется четырехсвязное соседство. Соседи для точки-затравки просматриваются в последовательность: верхний, нижний, правый, левый. Если верхний сосед не закрашен и нет признака верхней группы, то адрес этого соседа записывается в стек и устанавливается признак верхней группы. Если верхний сосед не закрашен, но есть признак верхней группы, то его адрес в стек не записывается. Если нижний сосед не закрашен и нет признака нижней группы, то адрес этого соседа записывается в стек и устанавливается признак нижней группы. Если нижний сосед не закрашен, но есть признак верхней группы, то его адрес в стек не записывается. Если левый сосед не закрашен, то он закрашивается и его адрес запоминается как адрес левого соседа. 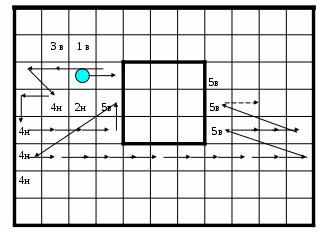 Рис. Заливка с затравкой.‑40 Если правый сосед не закрашен, то он закрашивается, устанавливается признак движения вправо и осуществляется переход к обработке его правого соседа, которая выполняется аналогично обработке предыдущей точки. Если очередной правый сосед закрашен, то признаки верхней и нижней групп и признак правого движения сбрасывается и анализируется регистр адреса левого соседа, если он пуст, то осуществляется переход к следующей точке, адрес которой извлекается из стека. Если регистр левого соседа не пуст, то устанавливается признак движения влево и начинается движение влево, при котором выполняются действия, аналогичные описанным с той лишь разницей, что правый сосед не анализируется. Если при движении влево очередная точка не является не закрашенной точкой области, то признаки верхней и нижней групп и признак левого движения сбрасывается и осуществляется переход к следующей точке, адрес которой извлекается из стека. Обработка следующей точки выполняется аналогично обработки точки-затравки. Заливка с затравкой с запоминанием соседних групп требует существенно меньший объем стека, чем просто заливка с затравкой. Однако ее процедуры сложнее, чем в случае заливки без запоминания соседних групп. 5 ПРЕОБРАЗОВАНИЕ КООРДИНАТПреобразование координат является одной из широко используемых функций в машинной графики, применяемой при решении многих задач. В качестве примера можно рассмотреть задачу отсечения отрезка многоугольным окном. Помимо использования алгоритма Кируса-Бека, данную задачу можно решить и другим путем. Рассмотрим один из них, в котором используется преобразование координат. Пусть заданы окно в виде невыпуклого многоугольник и отсекаемый отрезок, которые приведены на рис.5-1. 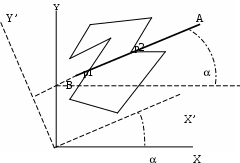 Рис.5-1 На рисунке приняты следующие обозначения: AB – отсекаемый отрезок; - угол наклона отрезка к координатной оси X; p1, p2 -точки пересечения заданного отрезка с многоугольником-окном. Для решения поставленной задачи повернем систему координат на угол «»против часовой стрелки так, чтобы заданный отрезок АВ оказался параллельным оси X в новой повернутой системе координат. При таком «особом» положении отсекаемого отрезка в новой системе координат, легко можно найти точки его пересечения с ребрами заданного многоугольного окна. Например, можно использовать подход, который описан в разделе «4.1 Заливка с сортировкой». Найдя в новой системе координат точки пересечения отрезка с ребрами рассматриваемого многоугольника, необходимо вернуться в исходную систему координат, повернув новую систему на угол «-». Таким образом, будут получены координаты точек пересечение заданного отрезка с ребрами окна в исходной системе координат, т.е. будет решена поставленная задача. |
