Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР. 1 отображение просранства пользователя и машинного носителя 4

• Название: 1 отображение просранства пользователя и машинного носителя 4
• Дата: 24.09.2022
• Размер: 1.86 Mb.
• Имя файла: Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР.doc
• Тип: Документы; #693275
• страница: 13 из 20

5.2 Преобразования в трех мерной системе координат

В трех мерной системе координат используются следующие базовые преобразования:

• 
  перенос точки на заданный вектор;
  
• 
  поворот на заданный угол относительно координатной оси;
  
• 
  перенос системы координат на заданный вектор;
  
• 
  поворот системы координат на заданный угол относительно координатной оси;
  
• 
  зеркальное отображение точки относительно координатной плоскости XY;
  
• 
  зеркальное отображение точки относительно плоскости XY;
  
• 
  зеркальное отображение точки относительно координатной оси XZ;
  
• 
  смена направление координатной оси;
  
• 
  изменение масштаба координат по оси X;
  
• 
  изменение масштаба координат по оси Y.
  
• 
  изменение масштаба координат по оси Z.
  

Перенос точки на вектор U, задаваемый параметрами u_x, u_y, u_z, предполагает следующее преобразование координат:
x_a’ = x_a - u_x;

y_a’ = y_a – u_y;

z_a’ = z_a – u_z.
Используя однородную систему координат, данные преобразования в матричной форме можно представить в виде:


где: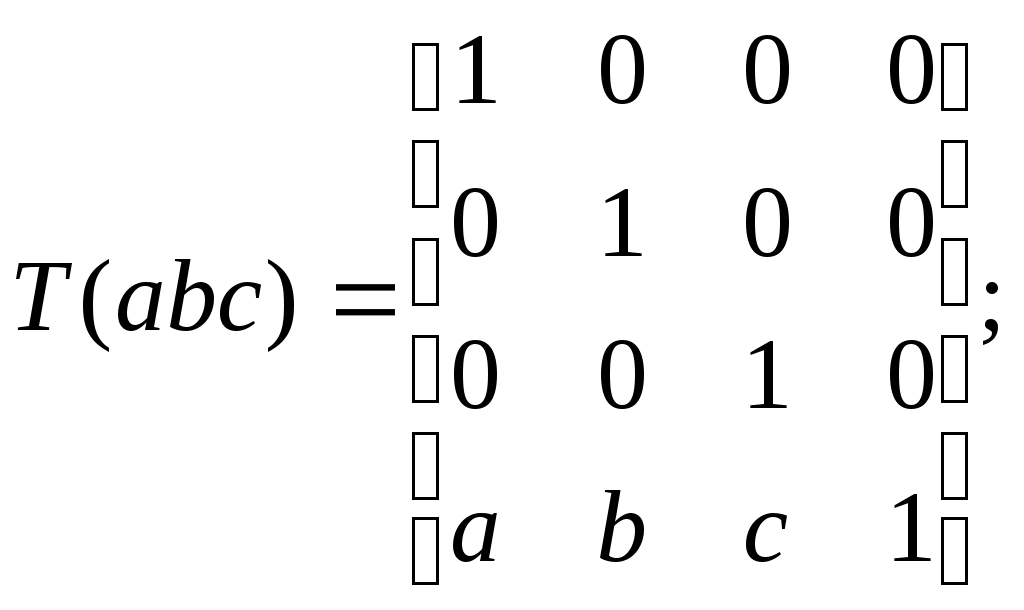



a,b,c – параметры вектора переноса.
Легко показать, что матрица обратного преобразования (или матрица переноса системы координат) в этом случае будет иметь вид: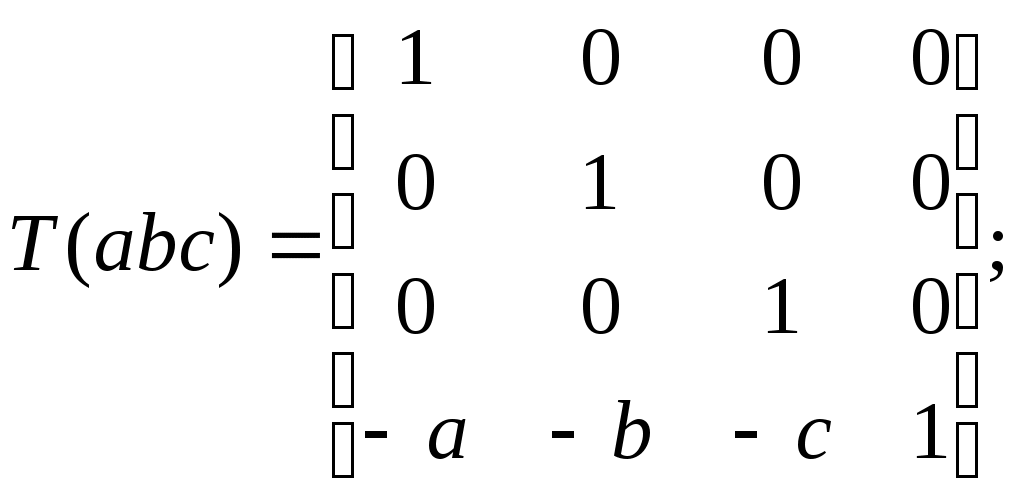


Поворот относительно координатной оси.

Поворот относительно оси Z.

Данный вид преобразования иллюстрируется ниже приведенным рисунком (Рис. Преобразования в трех мерной системе координат-50), где приводится поворот точки А на угол .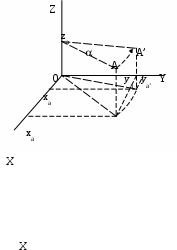



Рис. Преобразования в трех мерной системе координат‑50
Из приведенного рисунка видно, что поворот относительно оси Z не меняет координаты точки по координатной оси Z. Что же касается изменений координат по оси X и Y, то они аналогичны изменениям по осям X,Y в двумерной координатной системе, так как новая и старая точки остаются в одной плоскости, параллельной координатной плоскости X,Y. Таким образом, использую уравнения (5.1-5) и (5.1-6), будем иметь:
x_b’= x_b cos  - y_b sin  + 0;

y_b’= x_b sin  + y_b cos  +0;

z_b’= 0 +0 +z.
Данные преобразования можно представить в матричной форме как: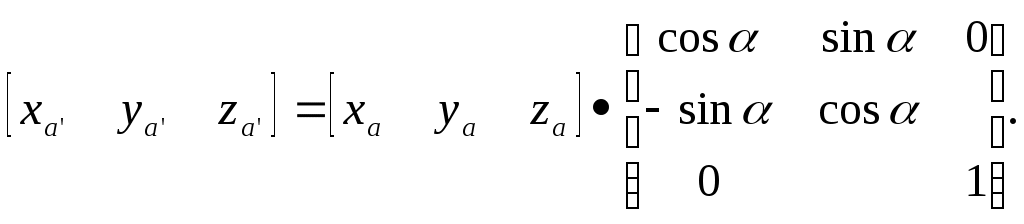
(5.1-7)

Поворот относительно оси X.

Координатные оси в трехмерной системе равнозначны, поэтому поворот относительно координатной оси X, аналогично повороту относительно оси Z, можно представить как:
y_b’= y_b cos  - z_b sin  + 0;

z_b’= y_b sin  + z_b cos  +0;

x_b’= 0 +0 +x.
Соответственно в матричной форме будем иметь: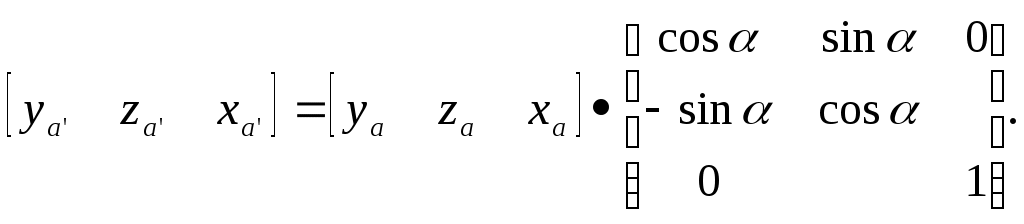

Для того, чтобы координаты матриц перечислялись в том же порядке, что и в выражении (5.1-7), необходимо их циклически сдвинуть в сторону элемента с большим индексом, т.е. вправо. При этом соответствующий сдвиг необходимо выполнить и в матрице начальных координат. Что же касается двумерной матрице, то ее колонки необходимо циклически сдвинуть вправо (в сторону колонки с большим индексом), а затем циклически сдвинуть строки вниз (в сторону строки с большим индексом), как это показано ниже.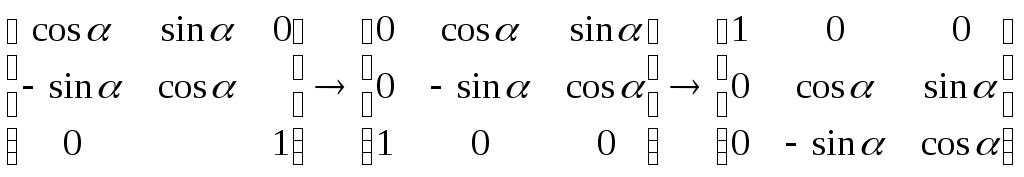
(5.1-8)
Поворот относительно оси Y.

Координатные оси в трехмерной системе равнозначны, поэтому поворот относительно координатной оси Y, аналогично повороту относительно оси Z, можно представить как:


z_b’= z_b cos  - x_b sin  + 0;

x_b’= z_b sin  + x_b cos  +0;

y_b’= 0 +0 +y.
Соответственно в матричной форме будем иметь: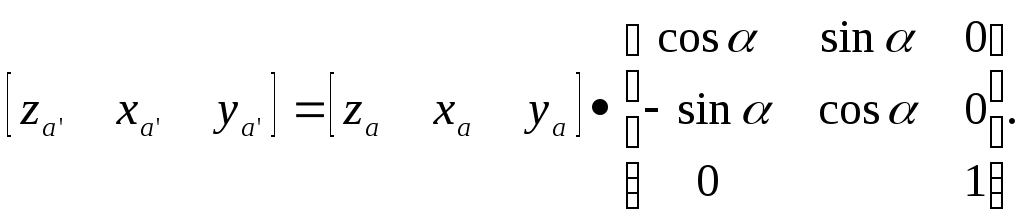

Для того, чтобы координаты в матрице перечислялись в том же порядке, что и в выражении (5.1-7), необходимо их циклически сдвинуть в сторону элемента с меньшим индексом, т.е. влево. При этом соответствующий сдвиг необходимо выполнить и в матрице начальных координат. Что же касается двумерной матрице, то ее колонки необходимо циклически сдвинуть влево (в сторону колонки с меньшим индексом), а затем циклически сдвинуть строки вверх (в сторону строки с меньшим индексом), как это показано ниже.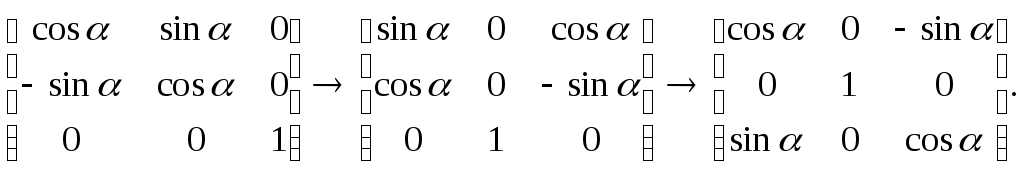

(5.1-8),
Таким образом, матрицы базового поворота на угол  по отношения к координатной оси будут иметь вид: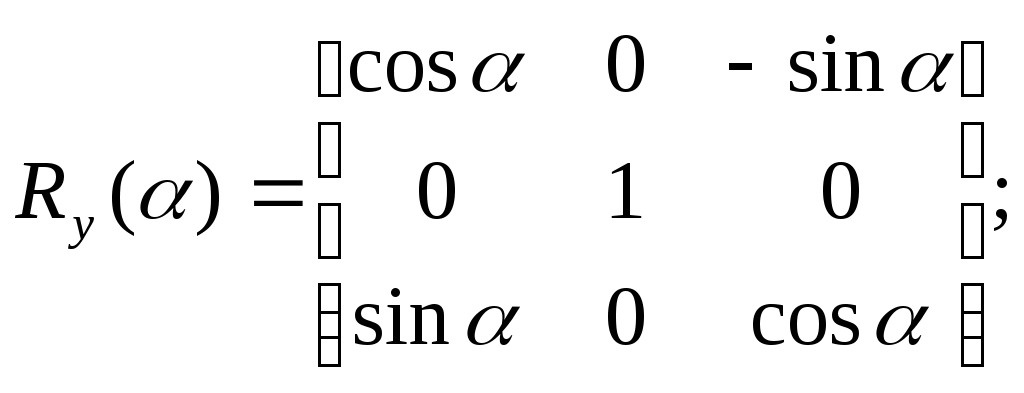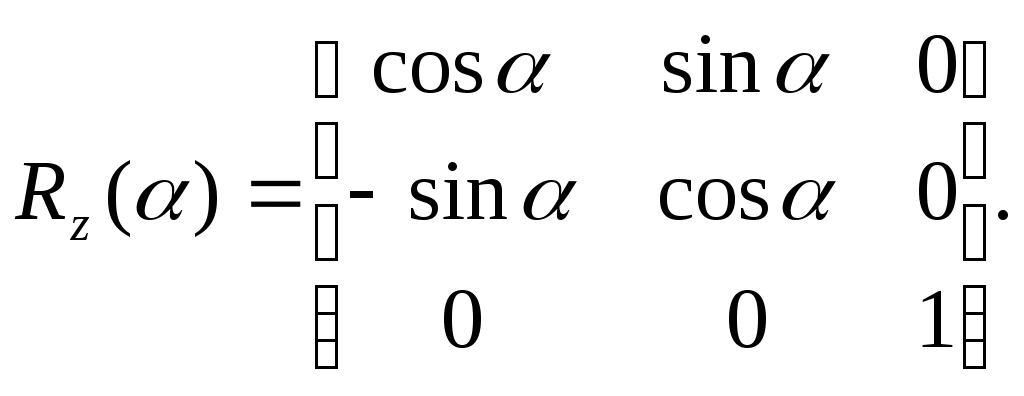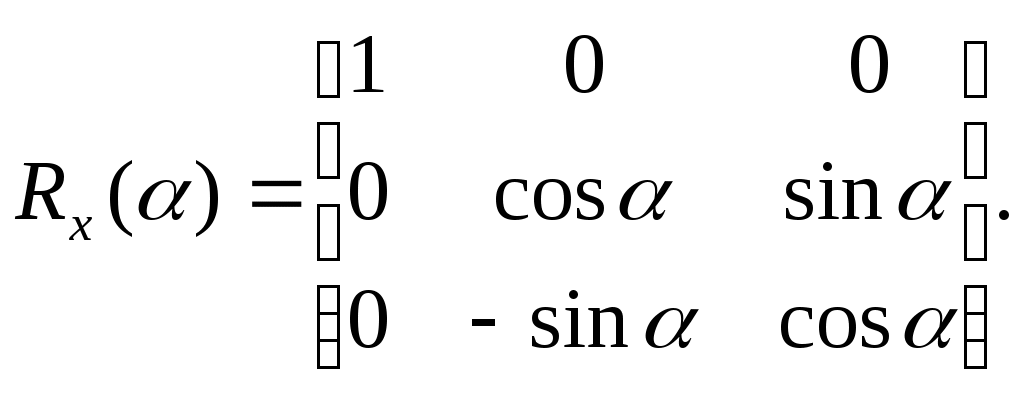
(5.1-9),
Легко показать, что матрицы соответствующих обратных преобразований (или матрицы поворота системы координат относительно координатных осей), будут иметь вид: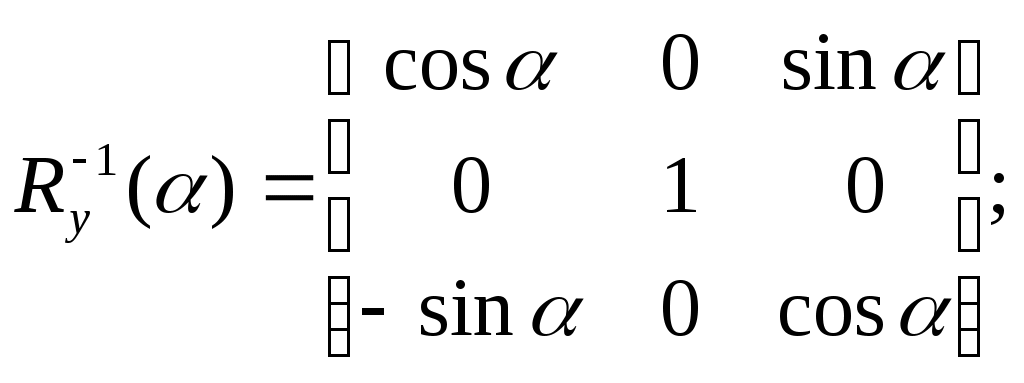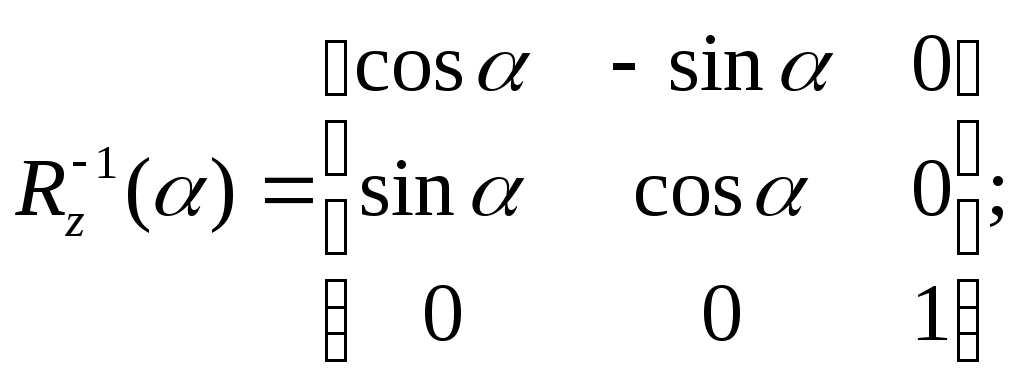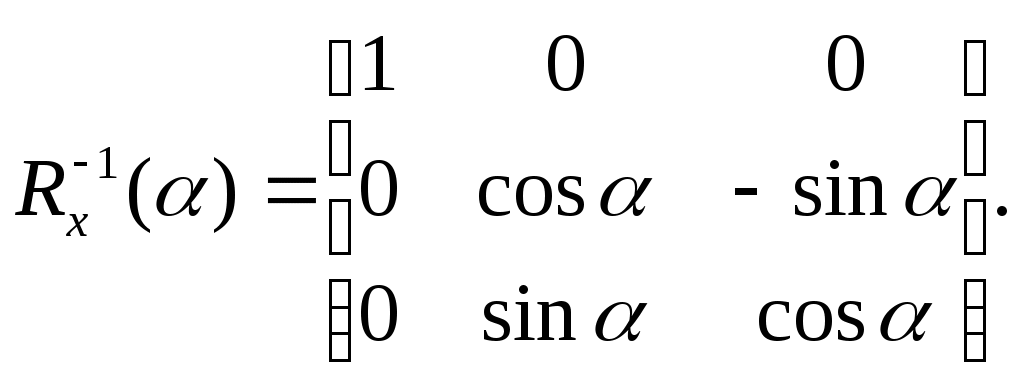
(5.1-10)
Зеркальное отображение точки относительно координатной плоскости XY.

Преобразования этого типа предполагает следующиезависимости координат.

Для отображения относительно координатной плоскости XY:
x_a’ = x_a

y_a’ = y_a ;

z_a’ = -z_a .
В матричной форме это преобразование записывается как: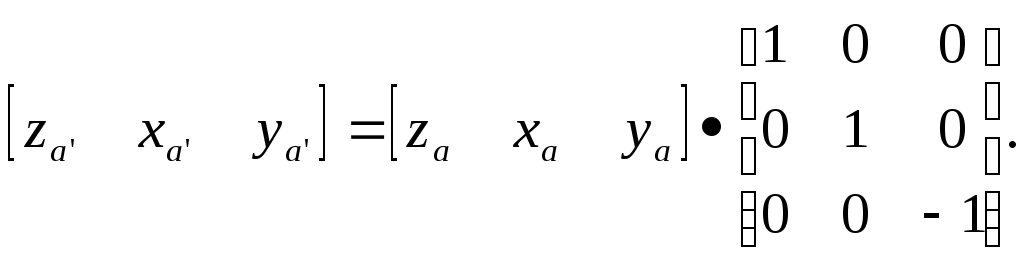

Для отображения относительно координатной плоскости XZ;

x_a’ = x_a

y_a’ = - y_a ;

z_a’ = z_a

В матричной форме это преобразование записывается как: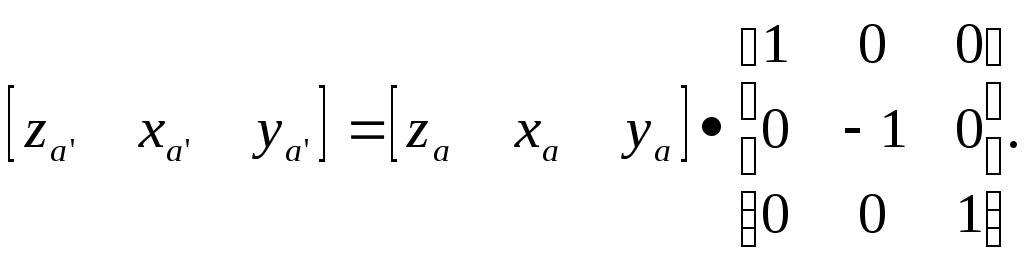


Для отображения относительно координатной плоскости ZY:

x_a’ = -x_a

y_a’ = y_a ;

z_a’ = z_a .

Матричная запись будет иметь вид: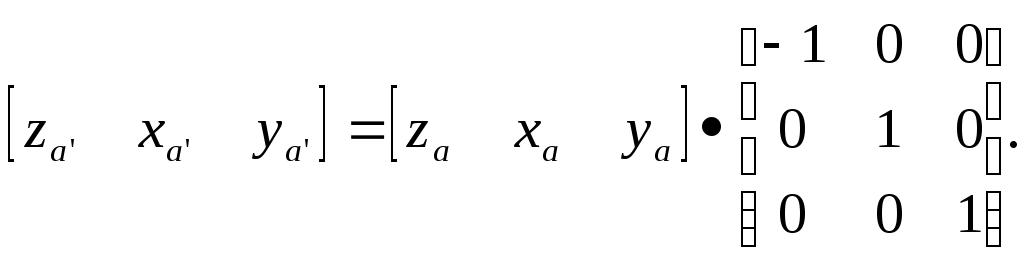

Смена направления координатной осей

Преобразование координат при смене направленности координатных осей X,Y,Z отображается, соответственно, следующими матрицами.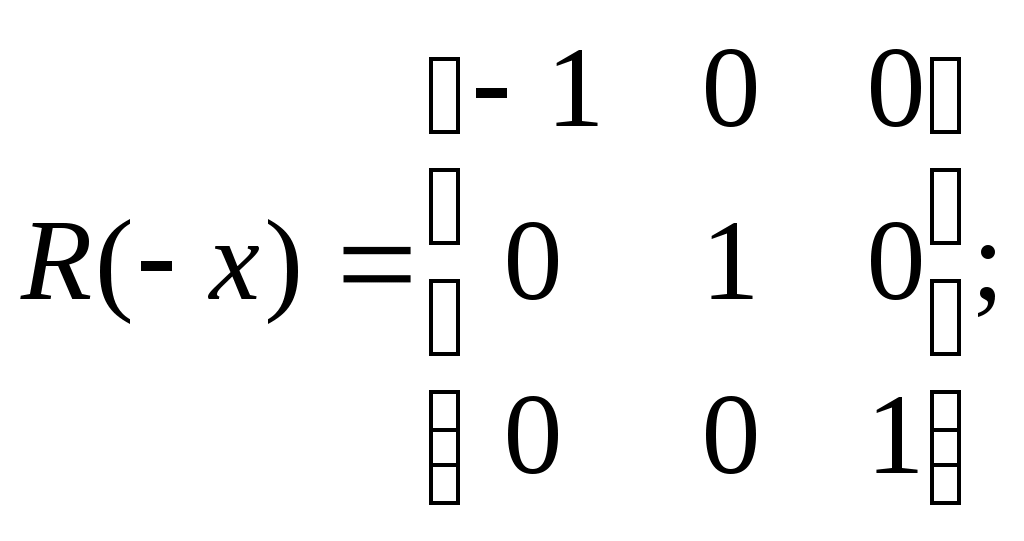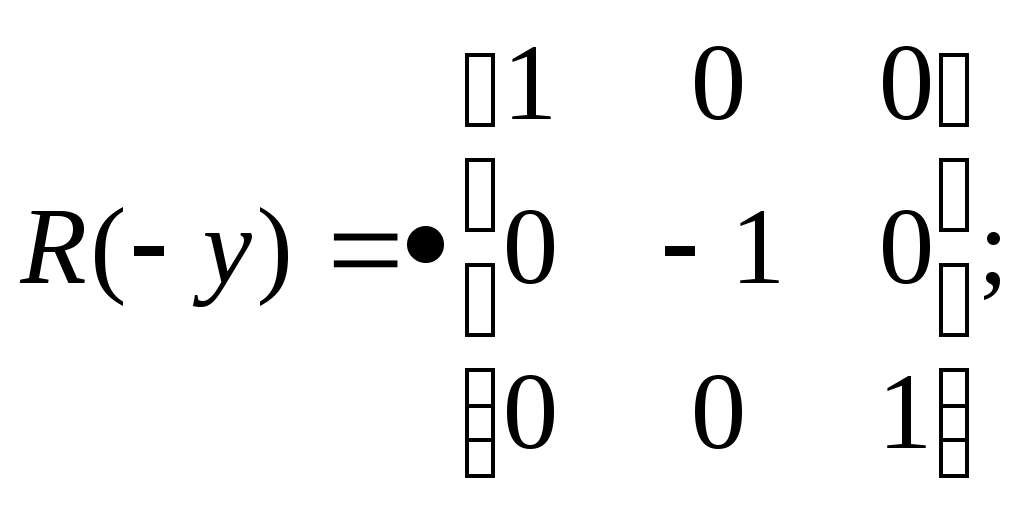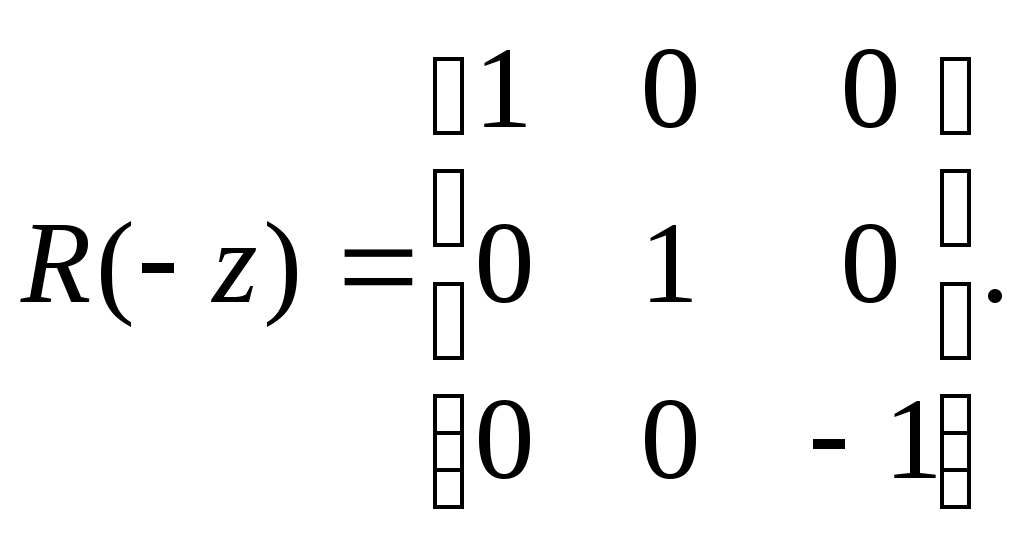

Изменение масштаба по координатным осям.

Преобразования этого типа предполагает следующиезависимости координат:

x_a’ = r x_a;

y_a’ = l y_a ;

z_a’ = f z_a,

где r, l, f – вводимые масштабные коэффициенты по соответствующим координатным осям.
В матричной форме это преобразование записывается как:


где: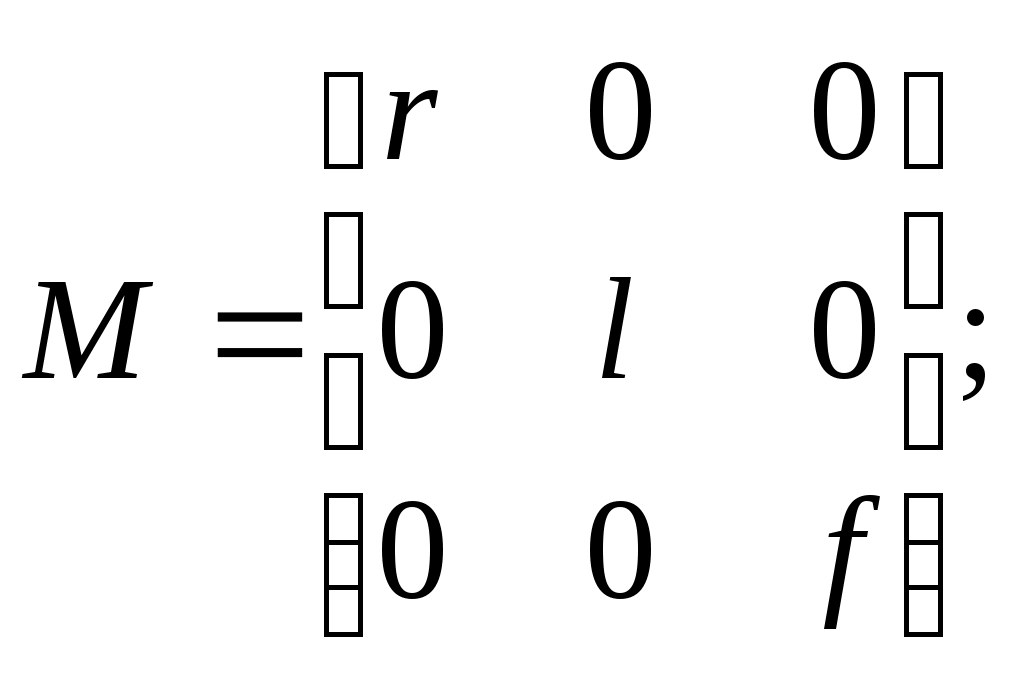


Рассмотрим сложное преобразование координат в трехмерной системе.

Предположим необходимо выполнить поворот точки относительно произвольного вектора в трех мерной системе координат, как это показано на .

Сначала решим рассматриваемую задачу для частного случая. Предположим, что вектор U, относительно которого нужно повернуть точку А на угол , проходит через начало системы координат (Рис. Преобразования в трех мерной системе координат-52).

Вектор, относительно которого необходимо выполнить поворот, можно задать в сферических координатах, т.е. через тройку параметров:  где:

• 
  - модуль вектора U;
  
• 
   - угол между вектором Uи координатной осью Z;
  
• 
   - угол между проекцией ’ вектора U на координатную плоскость XY и координатной осью X.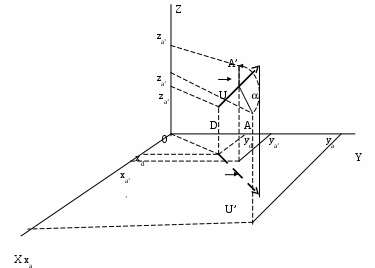
  

Рис. Преобразования в трех мерной системе координат‑51
При таком частном случае заданное преобразование поворота точки относительно заданного вектора можно выполнить за счет последовательности следующих базовых преобразований:

1. 
   поворот исходной системы координат относительно координатной оси Z на угол ;
   
2. 
   поворот новой системы координат относительно оси Y на угол-;
   
3. 
   поворот точки А относительно координатной оси Z’’на угол ;
   
4. 
   поворот системы координат на угол  относительно оси Y;
   
5. 
   поворот системы координат относительно координатной оси Z на угол-.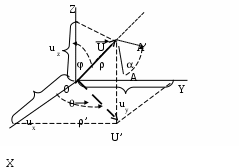
   

Рис. Преобразования в трех мерной системе координат‑52
1-ый поворот исходной системы координат относительно ее оси Z на угол  формирует новую систему координат X’Y’Z’, в которой ось X’ совпадет с ’, ось Y’ будет повернута по отношению к оси Y на угол , ось Z’ совпадает с осью Z, что показано на Рис. Преобразования в трех мерной системе координат-53.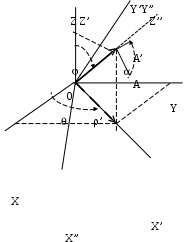


Рис. Преобразования в трех мерной системе координат‑53
Отметим, что в новой системе координат вектор U лежит в координатной плоскости X,Z.

Поворот осуществляется при использовании матрицы обратного преобразования типа «поворот относительно координатной оси Z».

2-ой поворот формирует систему координат X”Y”Z”, в которой ось X” повернута относительно оси X’ на угол ( -) угол поворота отрицательный, так как для совмещения оси Z новой системы координат с вектором U поворот нужно выполнить в направлении по часовой стрелке), ось Y’’ совпадает с осью Y’, ось Z” совпадает с вектором U.

Рассматриваемому повороту соответствует матрица базового поворота точки относительно оси Y.

3-ий поворот. В системе координат, полученной после выполнения двух предыдущих поворота, заданный вектор U совпадает с осью Z”, что позволяет выполнить в этой системе заданный поворот за счет базового поворота относительно оси Z”.

4-ый поворот обеспечивает возврат к системе координат X’,Y’,Z’ и реализуется с помощью матрица обратного преобразования типа «поворот относительно координатной оси Y» на угол .

5-ый поворот обеспечивает возврат к начальной системе координат X,Y,Z и реализуется с помощью матрица преобразования типа «поворот относительно координатной оси Z» на угол -.

Таким образом, формирование координат точки при рассматриваемом сложном преобразовании осуществляется через произведение матриц элементарных преобразований следующего вида:
(5.1-10)

где:

• 
  x_и, y_и, z_и – исходные кордиинаты точки;
  
• 
  x_пч, y_пч, z_пч – новые кордиинаты после поворота для рассматриваемого частного случая;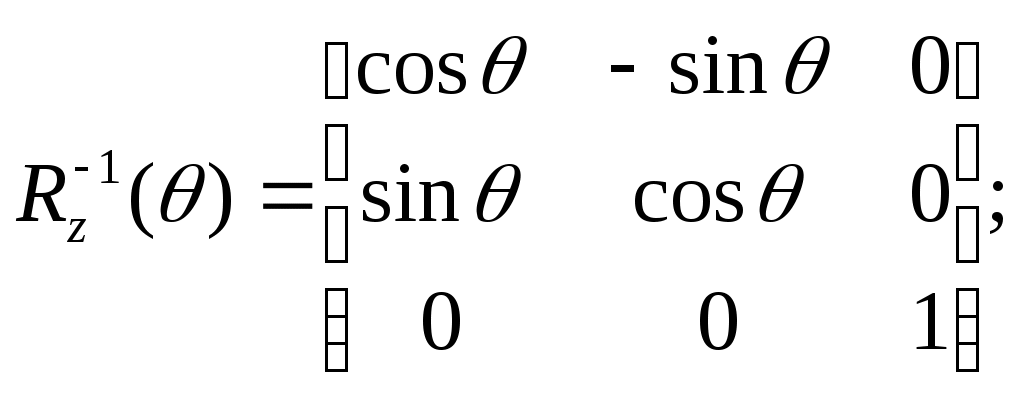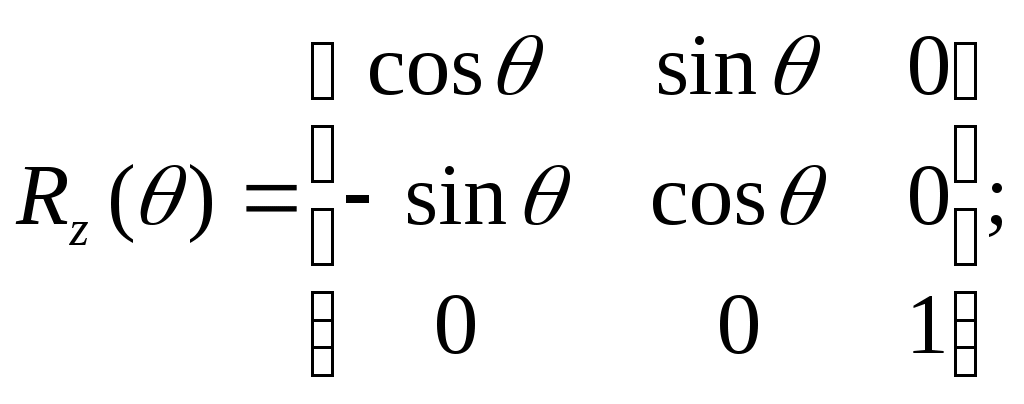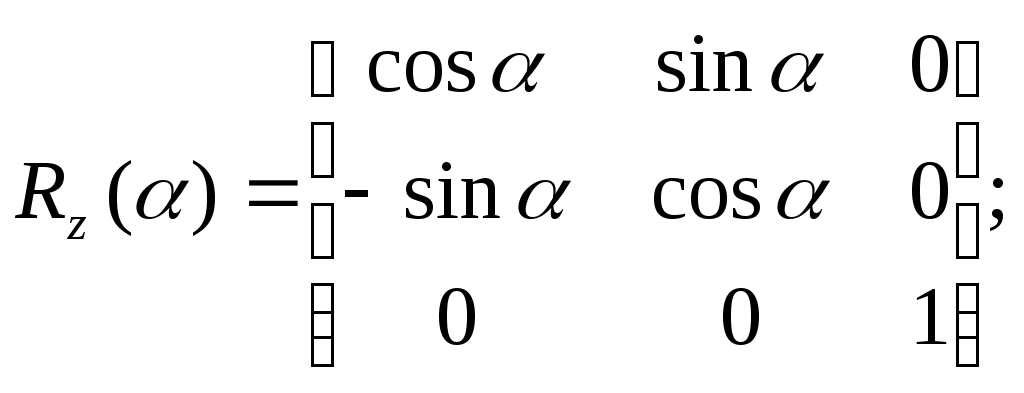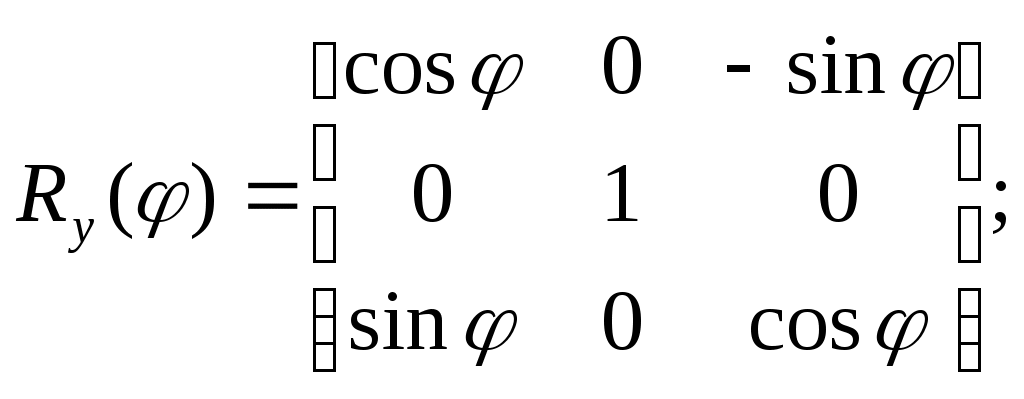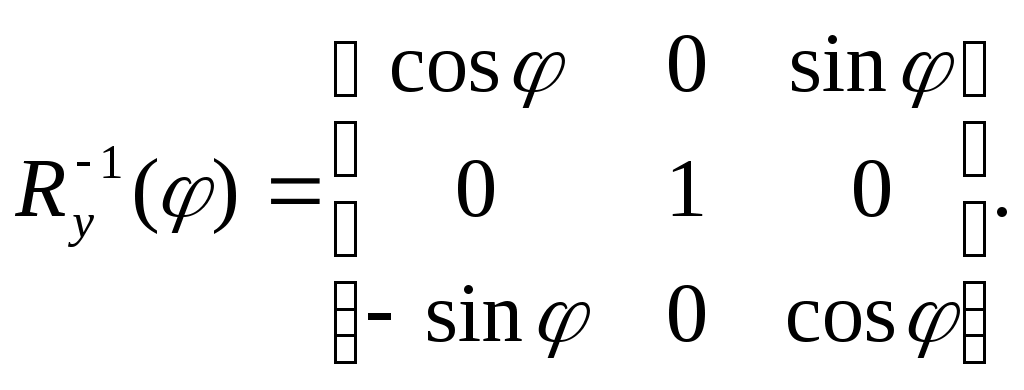
  
• 
  
  
• 
  
  
• 
  
  
• 
  
  

-
При решении рассматриваемой задачи для общего положения в пространстве вектора U, используется те же действия, что и в рассмотренном частный случай, с добавлением в начале преобразований перенос исходной системы координат в точку D (см Рис. Преобразования в трех мерной системе координат-50) и в конце - перенос начало координат из точки D в точку начала координат исходной системы.

Таким образом, для общего положения вектора поворота, новые координаты точки А после заданного поворота определяются через произведение матриц элементарных базовых преобразований следующим образом:
(5.1-11)

где:

x_п, y_п, z_п - координаты положения точки после поворота;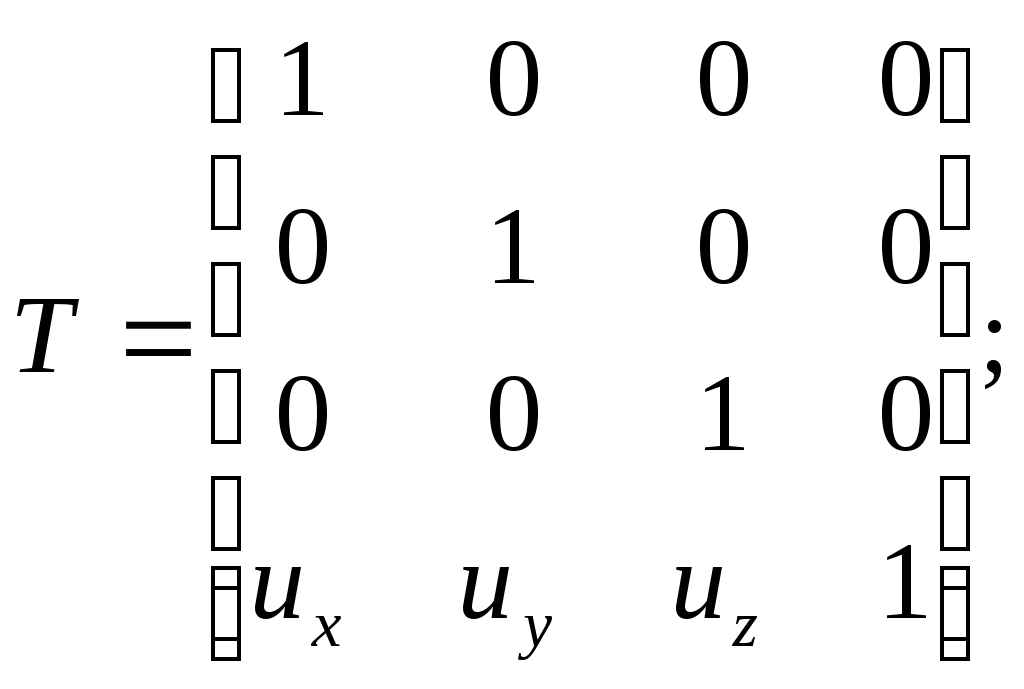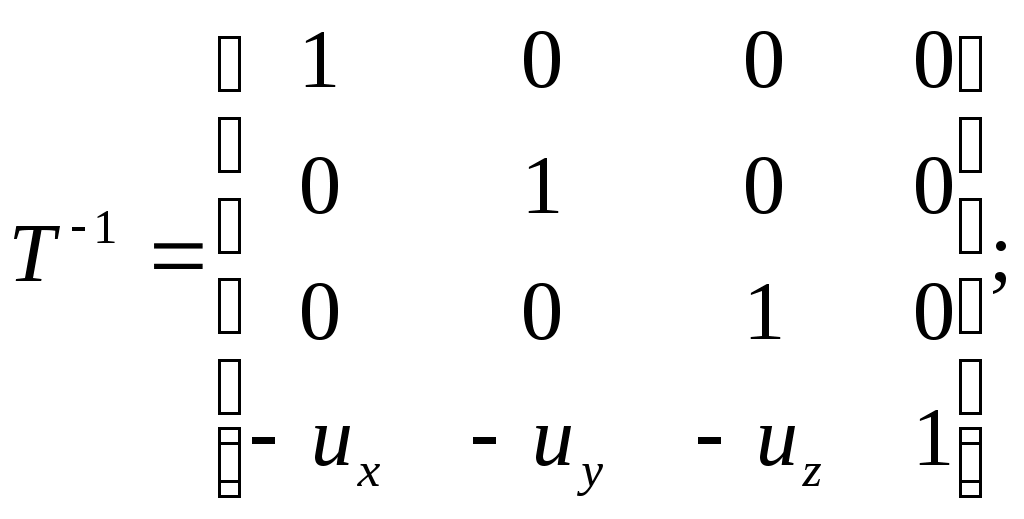



Переход от одной формы задания вектора к другой.

Вектор, который часто используется в процессе преобразований координат, иногда удобно задавать в полярных координатах (например, при поворотах), а иногда в декартовых координатах (например, при переносах). На практике вектор задается только одним из этих способов. Для перехода от одной формы задания вектора к другой используются следующие соотношения.

Переход от декартового к полярному представлению вектора

При задании вектора U в полярных координатах в виде тройки { как следует из Рис. Преобразования в трех мерной системе координат-52, имеет место:
u_z=cos;

u_x=sin  cos ;

u_y=sin  sin ;
Переход от полярного к декартовому представлению вектора

При задании вектора U в декартовых координатах в виде тройки {u_x u_y u_z как следует из Рис. Преобразования в трех мерной системе координат-52, имеет место:



arc cos(u_z./);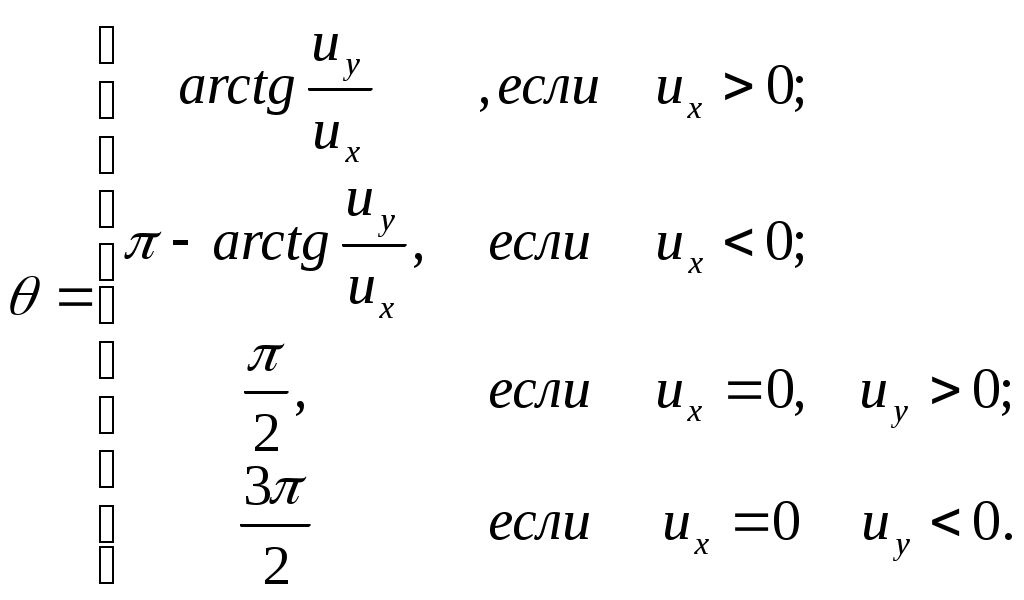


В выражении (5.1-11) в качестве сомножителей выступают матрицы разных размерностей (3*3 и 4*4). Для того, чтобы найти их произведение, необходимо привести матрицы к одной размерности, т.е. матрицы размерности 3*3 необходимо расширить до размерности 4*4. Однако с расширением размерности не надо спешить. Пользуясь свойством ассоциативности произведения матриц, умножение матриц следует выполнять в последовательности, определенной скобками в ниже приведенной версии выражения (5.1-11):
(5.1-12)

Обозначение матрицы знаком «*» означает использование расширенной матрицы.

Такой прием позволяет уменьшить затраты времени на выполнение умножений матриц.

В выражении (5.1-11) произведение первых трех матриц обеспечивает переход от исходной системы координат к системе координат, «удобной» для заданного преобразования. Что касается произведения последних трех матриц, то они обеспечивают переход от «удобной» системы координат к исходной. По этому, используя свойство ассоциативности, выражение (5.1-11) можно представить как:
(5.1-13)

где

• 
  R1 – матрица перехода от исходной к «удобной» системе координат;
  
• 
  R1^-1 –матрица, обратная матрице R1.
  

В некоторых случаях, с точки зрения затрат времени, реализация выражения (5.1-12), может быть предпочтительнее, чем реализация выражения (5.1-11). В свою очередь, может оказаться удобнее формировать матрицу R1^-1 не через произведение трех матриц (см. выражение(5.1-13), а получить ее, рассчитав ее элементы как элементы матрицы, обратной матрице R1.

Матрица, обратная заданной, может быть найдена следующим образом.

Из определения обратной матрицы следует, что матрица В является обратной по отношению к заданной матрице А, если имеет место равенства:
А*B=E,

где Е – единичная матрица, имеющая вид: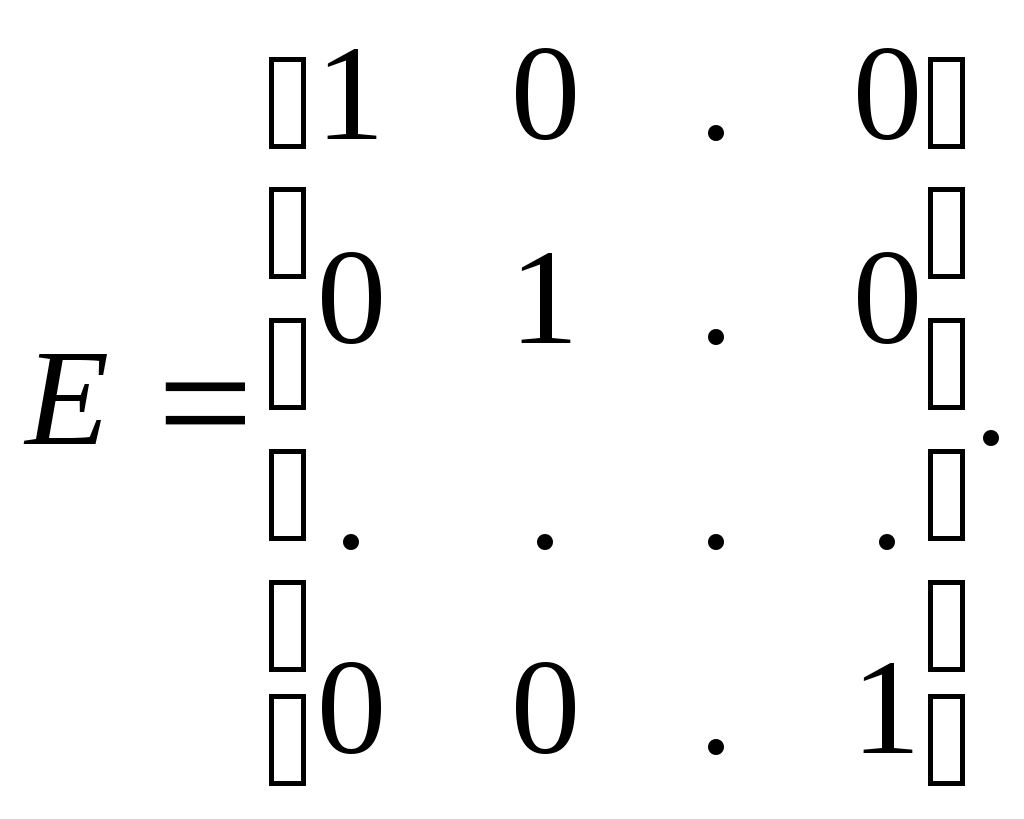


Отсюда элементы обратной матрицы могут быть найдены из системы уравнений: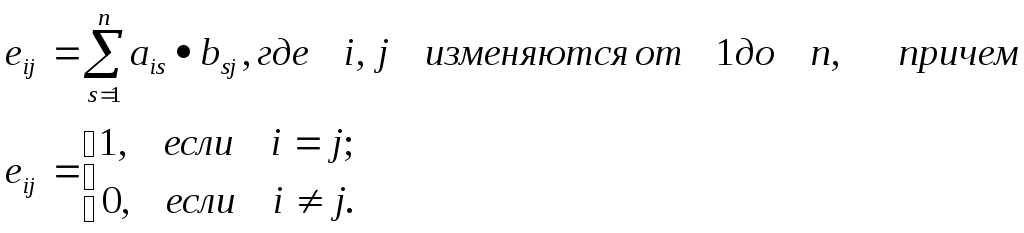