Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР. 1 отображение просранства пользователя и машинного носителя 4

• Название: 1 отображение просранства пользователя и машинного носителя 4
• Дата: 24.09.2022
• Размер: 1.86 Mb.
• Имя файла: Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР.doc
• Тип: Документы; #693275
• страница: 16 из 20

6.5 Построение проекций трехмерных объектов

Задание объектов для проецирования.

Задание объектов для проецировании осуществляется несколькими множествами:

• 
  множество узловых точек Т;
  
• 
  множество ребер R;
  
• 
  множество граней G;
  
• 
  множество очерков O.
  

Множество точек.

Узловые точки объектов задаются, как правило, в абсолютных координата, т.е. множество точек включает описание координат всех узловых точек:

T ={ t₁, t₂, t₃,.. t_i,... t_n,},

где описание точки t_i представляется ее тремя координатами {x_i, y_i, z_i}. Например, для трехмерной сцены, приведенной на , множество узловых точек может быть задано матрицей, приведенной в виде :

Табл. Построение проекций трехмерных объектов‑2

Номера точек (индексы)	Координаты точки ti
	x	y	z
1	0	0	1
2	0	1	1
3	1	1	1
4	1	1	0
5	0	0	0
6	0	1	0
7	1	1	0
8	1	0	0
9	2	0	1
10	2	0	0
11	2	1	0
12	3	0	0

Первая колонка приведенной таблицы содержит номера, которыми помечены узловые точки сцены на . Эти номера совпадают с индексами элементов матрицы точек Т, содержащей описание множества узловых точек.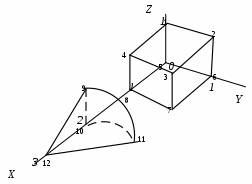



Рис. Построение проекций трехмерных объектов‑64
Множество ребер R.

Множество ребер содержит описание всех ребер объектов, представленных в трехмерной сцене. Это множество может быть организованно в виде матрицы, каждый элемент которых описывают одно из ребер. Описание ребер, как правило, включает задание начальной и конечной точек ребра и информацию о виде линии, несущей ребро (например, прямая, окружность, парабола и.п.). Вид несущей линия задается в виде уравнения этой линии. Задание начальной и конечной точек выполняется в виде ссылок на матрицу узловых точек. Например, для сцены на матрица ребер объектов сцены будет иметь вид, приведенный в -3.

Табл. Построение проекций трехмерных объектов‑3

№ элемента	Узловые точки (индексы матрицы элементов T)		Описание несущей линии
1	2	1	прямая
2	6	2	прямая
3	6	5	прямая
4	5	1	прямая
5	4	1	прямая
6	8	4	прямая
7	8	5	прямая
9	3	2	прямая
10	7	3	прямая
11	7	6	прямая
12	4	3	прямая
13	8	7	прямая
14	11	9	окружность
15	11	10	окружность
16	10	9	окружность
17	12	9	прямая
18	12	10	прямая
19	12	11	прямая

Множество граней.

Во множестве граней представлены описания всех граней объектов сцены в виде перечня ребер, составляющих контур каждой грани, и информации, характеризующую вид поверхности, несущую данную грань. Ребра грани задаются в виде ссылок на матрицу граней. Они перечисляются в порядке их расположения в контуре соответствующей грани. Желательно, чтобы порядок перечисление ребер, составляющих контур, для всех граней должен быть один и тот же, например, против часовой стрелки при рассмотрении грани со стороны внешней нормали к этой грани.

Для приведенной сцены описание граней может быть представлено в виде, приведенном в Табл. Построение проекций трехмерных объектов-4.
Табл. Построение проекций трехмерных объектов‑4

№ грани	Перечень ребер	Вид несущей поверхности
1	(1,2,3,4)	плоскость
2	4, 7, 6, 5	плоскость
3	12, 6, 13, 10	плоскость
4	12, 9, 1, 5	плоскость
5	7, 3, 11, 13	плоскость
6	11, 2, 9, 10	плоскость
7	14,15, 16	сфера
8	17,19, 14	плоскость
9	17,16,18	плоскость

Несущая поверхность задается в виде уравнения этой поверхности.

Процесс построения проекции объектов, как правило, выполняется в два этапа:

• 
  построение проволочная модель объектов;
  
• 
  удаление невидимые ребра.
  

Проволочная модель объекта представляет собой этот же объект, но у него все грани считаются прозрачными. Построение проволочной модели осуществляется за счет отображения всех ребер, имеющихся в соответствующей матрице ребер (Рис. Построение проекций трехмерных объектов-65).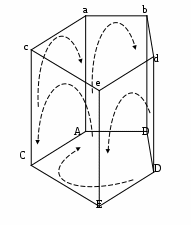




Рис. Построение проекций трехмерных объектов‑65
Удаление очевидно невидимых ребер

Удаление невидимых ребер в общем случае является сложной задачей, особенно если объекты имеют не плоские грани.

Прежде всего, необходимо определить и выбросить из проволочной модели очевидно невидимые ребра. Эта процедура выполняется следующим образом.

Если при задании грани в видовой системе координат ее ребра перечислялись в порядке их обхода в направлении против часовой стрелки, при взгляде на грань со стороны внешней нормали, то направление обхода ребер этой грани на плоскости проекции можно использовать для определения «тыльных (невидимых)» и «фронтальных (видимых)» граней на плоскости проекции. При этом:

• 
  если направление обхода ребер грани на плоскости проекции осуществляется против часовой стрелке, то это означает, что данная грань является фронтальной, то есть видимой при заданной проекции;
  
• 
  если направление обхода ребер грани на плоскости проекции осуществляется по часовой стрелке, то это означает, что данная грань является тыльной, то есть не видимой при заданной проекции.
  

Очевидно, что если ребро принадлежит двум тыльным (невидимым) граням, то это ребро очевидно невидимо. Следовательно такие ребра необходимо из проволочной модели удалить.

В результате удаления очевидно невидимых ребер, проволочная модель на Рис. Построение проекций трехмерных объектов-65 превращается в проекцию объекта, приведенную на Рис. Построение проекций трехмерных объектов-66.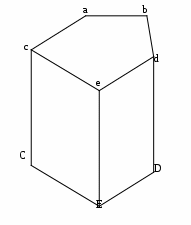




Рис. Построение проекций трехмерных объектов‑66
Определение направления обхода ребер

Определение направления обхода ребер грани осуществляется за счет использования векторного произведения двух векторов, в качестве которых используются два ребра, образующих угол грани (Рис. Построение проекций трехмерных объектов-67).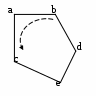



Рис. Построение проекций трехмерных объектов‑67
На приведенном рисунке, чтобы определить в каком направлении выполняется обход угла, если идти от ребра «ba» к ребру «aс», необходимо найти векторное произведение векторов bа и ас и определить его знак. Если знак векторного произведения положительный, то обход выполняется против часовой стрелке, если знак отрицательный, то это означает обход по часовой стрелке.

Для определения знака векторного произведения используется определитель, рассмотренный в разделе «3.3 Определение выпуклости многоугольника».

Данный подход определения невидимых граней можно использовать и в случае, когда плоские грани представлены невыпуклыми многоугольниками. В этом случае перед проецированием, необходимо в описании грани отметить для одного угола направление обхода составляющих его ребер и выполнить проверку направления обхода этих ребер на плоскости проекции. Если направление обхода граний на плоскости проекции и направление их обхода, указанное в описании грани, одинаковые, то грань является фронтальною, в противном случае, если направление обхода грани на проекции изменилось, то данная грань является очевидно не видимой.

Если объект выпуклый и имеет плоские грани, то после удаления явно невидимых граней процедура построения проекции объекта считается законченной. Для объектов, которые не относятся к этой категории, после выбрасывания явно невидимых ребер, возникает задача определения затенения ребер гранями переднего плана.