Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР. 1 отображение просранства пользователя и машинного носителя 4

• Название: 1 отображение просранства пользователя и машинного носителя 4
• Дата: 24.09.2022
• Размер: 1.86 Mb.
• Имя файла: Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР.doc
• Тип: Документы; #693275
• страница: 17 из 20

6.6 Затенение отрезка плоскостью при перспективной проекции

П ри отображении проекции трехмерных объектов возникает проблема затенения объектов заднего плана объектами переднего плана. Эту задачу в конечном плане всегда можно свести к задаче затенения отрезка треугольником.

Графически эту задачу можно представить, как это показано на .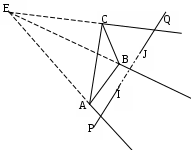

.


Рис. Затенение отрезка плоскостью при перспективной проекции ‑68
На приведенном рисунке в видовой системе координат с началом в точке Е представлен треугольник ABC и отрезок PQ. И требуется определить часть заданного отрезка, которая затеняется плоским треугольником.

Очевидно, что затеняется та часть отрезка, которая находится во внутренней области бесконечной треугольной усеченной пирамиды с верхней гранью в виде треугольника ABC. На приведенном рисунке это отрезок IJ.

Задача в общем случае решается в два этапа:

• 
  на первом определяется точки пересечения отрезка с боковыми гранями бесконечной треугольной пирамиды с вершиной в точке Е, ребра которой проходят через точки А, В, С, т.е. определяется часть отрезка, находящаяся внутри этой пирамиды;
  
• 
  на втором определяются пересечение найденного фрагмента отрезка с усеченной пирамидой.
  

Рассмотрим действия на этих этапах.

Первый этап.

В общем случае точек пересечения может быть одна (касание или отрезок одним концом находится внутри бесконечной пирамиды), две (отрезок пронизывает пирамиду) и ни одной (отрезок полностью находится внутри пирамиды или вне ее.

На рассматриваемом этапе поочередно ищутся точки пересечения отрезка с тремя гранями бесконечной пирамиды.

Рассмотрим этот процесс для грани бесконечной пирамиды, проходящей через точки А и В.

Сначала определим пересечение линии, несущей отрезок, с плоскостью, несущей рассматриваемую грань бесконечной пирамиды.

Для этого представим уравнение, описывающее линию, несущую отрезок PQ, следующим образом:


  

Т()= EP + r  , где:

Т() – векторное представление точки, принадлежащей прямой, проходящей через точки А и В. Координаты этой точки через параметр  определяются как:

x= x_p +r₁;

y= y_p +r₂;

z= z_p +r₃;

 

r – вектор, определяемый отрезком PQ, причем r =r₁,r₂,r₃, где:

r₁=x_Q- x_p;

r₂=у_Q- у_p;

r₃=z_Q- z_p;

x_Q, y_Q, z_Q; x_p, y_p, z_p – соответственно, координаты точек Q и P.



Зададим уравнение плоскости ЕАВ, проходящей через отрезок АВ и начало системы координат Е, т.е плоскости несущей рассматриваемую грань бесконечной треугольной пирамиды, в виде:

D₁x+ D₂y+D₃z +D = 0.

Определим коэффициенты D₁,D₂,D₃, D.

В общем случае уравнение плоскости, проходящей через три точки L, M, N можно представить в виде определителя: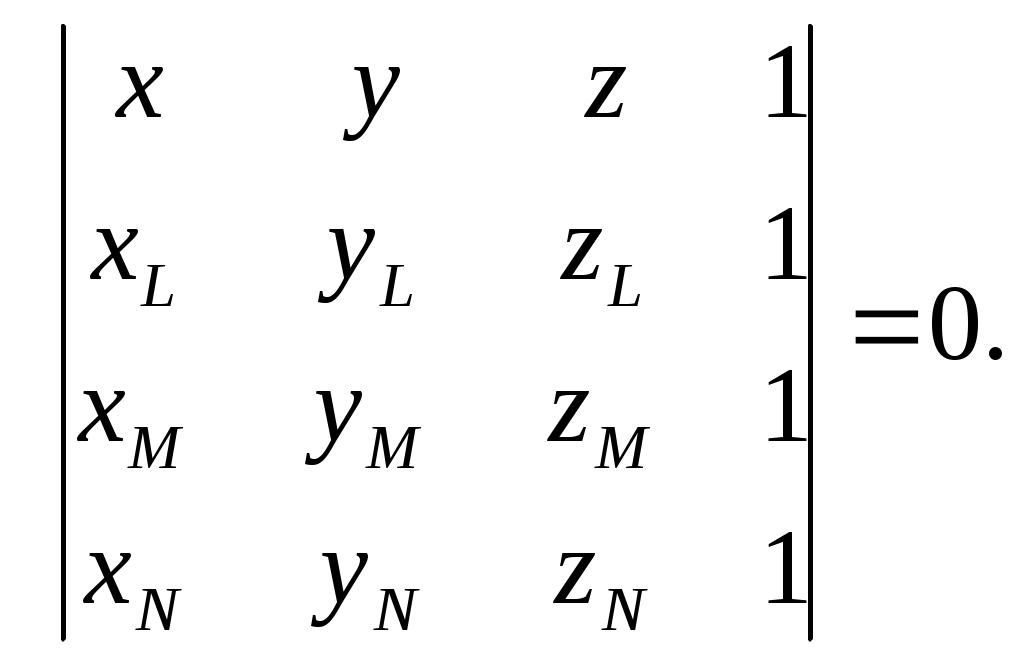

Для плоскости ЕАВ, проходящей через начало видовой системы координат, можно записать: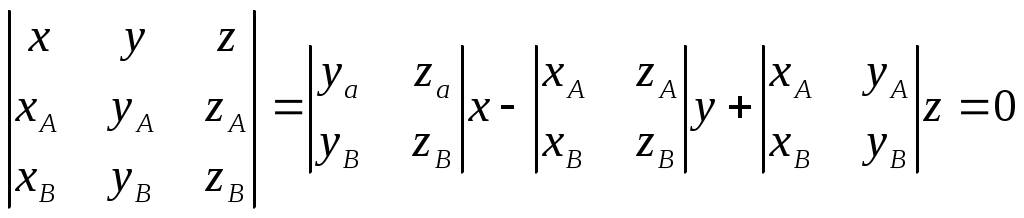

Отсюда, коэффициенты D₁,D₂,D₃ можно определить как:
D₁= x_Аz_B –y_Bz_А

D₂= x_Bz_А–x_Аz_B;

D₃= x_Аy_B –x_By_А.
Значение параметра, соответствующего точи пересечения рассматриваемых плоскости и отрезка, найдем, решив совместно уравнение прямой и уравнение плоскости с найденными коэффициентам D₁,D₂,D₃.
D₁(x_A +r₁) +D₂( y_A +r₂) +D₃(z_A +r₃) =0,


Искомая точка пересечения с рассчитанным значением параметра  будет принадлежать отрезку PQ, если будет выполняться условие:
0<=  <=1. (6.6-1)
Определим условия принадлежности найденной точки пересечения грани ЕАВ бесконечной треугольной пирамиды. Для этого найдем пересечение линии, несущей отрезок AB и плоскости ЕPQ, проходящей через точки Е, P, Q.

Представим уравнение линии, несущей отрезок АВ, в векторной параметрической форме:
  

Т()= EA + R , где:

• 
  Т() – векторное представление точки, принадлежащей прямой, проходящей через точки А и В. Координаты этой точки через параметр  определяются как:
  
• 
  x= x_p +R₁ ;
  
• 
  y= y_p +R₂;
  
• 
  z= z_p +R₃;
  
  • 
    
    
• 
  R – вектор, определяемый отрезком PQ, причем R =R₁,R₂,R₃, где:
  
• 
  R₁=x_B- x_A;
  
• 
  R₂=у_B- у_A;
  
• 
  R₃=z_B- z_A;
  
• 
  x_A, y_A, z_A; x_B, y_B, z_B – соответственно, координаты точек A и B.
  

Зададим уравнение плоскости ЕPQ, несущей PQ и проходящей через начало системы координат Е, в виде:

U₁x+ U₂y+U₃z = 0.

Определим коэффициенты U₁, U₂, U₃.

Уравнение плоскости ЕPQ, проходящей через начало видовой системы координат, можно, используя определитель, записать как: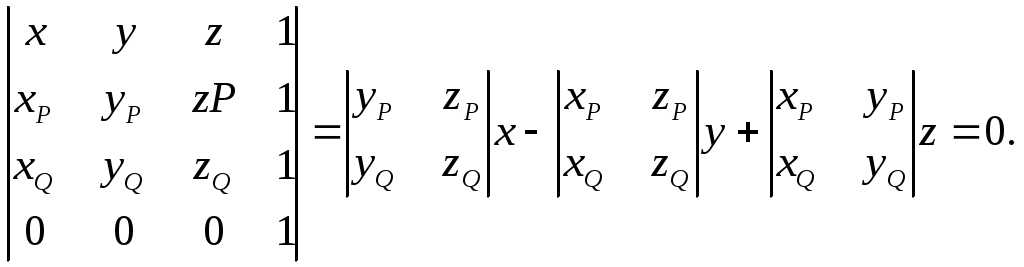

Отсюда, коэффициенты U₁, U₂, U₃ можно определить как:

U₁= x_pz_Q –y_Qz_P;

U₂= x_Qz_P–x_Pz_Q;

U₃= x_Py_Q –x_Qy_P.
Значение параметра, соответствующего точrи пересечения рассматриваемых плоскости и отрезка, найдем, решив совместно уравнение прямой АВ и уравнение плоскости с найденными коэффициентам D₁,D₂,D₃.
U₁(x_p +R₁) +U₂( y_p +R₂) +U₃(z_p +R₃) =0,


Искомая точка пересечения с рассчитанным значением параметра  будет принадлежать отрезку АВ, если будет выполняться условие:
0 <=  < =1. (6.6-2)
Таким образом, чтобы точка пересечения линии, несущей отрезок PQ и плоскости, несущей грань ЕАВ бесконечной пирамиды, была бы точкой пересечения отрезка PQ и грани пирамиды ЕАВ, необходимо одновременное выполнение условия (6.6-1) и (6.6-1).

Аналогичные расчеты необходимо сделать для всех остальных боковых граней заданной бесконечной пирамиды. Таким образом будет найдены точки I и J пересечения заданного отрезка и боковых граней бесконечной треугольной пирамиды.
Второй этап

Рассмотренным выше способом определяется уравнение плоскости, проходящей через точки А, В, С. Пусть это будет уравнение:
F₁x + F₂y+ F₃x + F = 0. (6.6-3)
Поочередно подставляя в найденное уравнение плоскости координаты точек E, I, J, рассчитываются значения h_E, h_I, h_J, определяющие положение точек E, I, J относительно плоскости, несущей верхнюю грань А В С рассматриваемой бесконечной усеченной пирамиды:

F₁x_Е + F₂y_Е+ F₃z_Е + F = h_Е;

F₁x_I + F₂y_I+ F₃z_I + F = h_I;

F₁x_J + F₂y_J + F₃x _J + F = h _J.

Если h_Е, h_I, h_J имеют один и тот же знак, то найденные точки I, J обе находятся перед верхней гранью АВС (). В этом случае можно сделать вывод, что отрезок PQ полностью виден.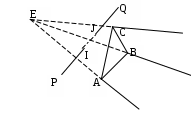



Рис. Затенение отрезка плоскостью при перспективной проекции ‑69
Если h_I, h_J имеют одинаковый знак и этот знак противоположен знаку h_Е, то это означает, что точки I, J располагаются за верхней гранью АВС и являются точками пересечения отрезком PQ c боковых граней бесконечной усеченной пирамиды, и часть заданного отрезка, ограниченная точками I,J, невидна (Рис. Затенение отрезка плоскостью при перспективной проекции -68).

Если h_I, h_J имеют разные знаки, то это означает, что точки I и J располагаются по разные стороны относительно верхней гранью АВС (Рис. Затенение отрезка плоскостью при перспективной проекции -70) В этом случае необходимо найти точку S пересечения отрезка PQ и плоскоси, несущей грань АВС, решив совместно уравнение плоскости, несущей грань АВС, и уравнение линии, несущей отрезок PQ.

Если точка I находится по одну сторону от треугольника АBC, что и точка Е, то невидимой чстью затеняемого отрезка PQ будет отрезок SJ. В противном случае невидимой чстью затеняемого отрезка PQ будет отрезок SI.


Q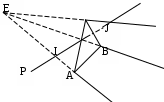




Рис. Затенение отрезка плоскостью при перспективной проекции ‑70
Как видно из выше описанного, в общем случае решение поставленной задачи довольно-таки сложно. Поэтому, прежде чем решать ее в общем случае, целесообразно проверить наличие в задании положения треугольника и отрезка частного случая.

Рассмотрим несколько таких частных случаев.

Частный случай 1. Отрезок находится перед треугольником АВС, а, следовательно, он полностью видим (Рис. Затенение отрезка плоскостью при перспективной проекции -71).

Для того чтобы определить наличие этого случая, достаточно проанализировать положение отрезка относительно плоскости, несущей треугольник АВС. Процедура в этом случае аналогична той, какая использовалась выше для опеделения положения точек I и J по отноiении к плоскости, несущей треугольник ABC.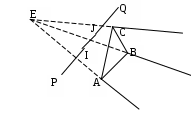



Рис. Затенение отрезка плоскостью при перспективной проекции ‑71
Частный случай 2. Отрезок находится вне рассматриваемой бесконечной пирамиды, а следовательно полностью видим (Рис. Затенение отрезка плоскостью при перспективной проекции -72).

Для того чтобы определить наличие этого случая необходимо для каждой боковой грани рассматриваемой бесконечной пирамиды проанализировать расположение точек P и Q по одну сторону и проверить будет ли эта сторона внешней. Если окажется, что заданный отрезок находится с внешней стороны относительно хотя бы одной грани, то отрезок полностью видим.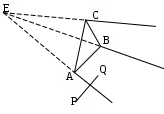



Рис. Затенение отрезка плоскостью при перспективной проекции ‑72
Частный случай 3. Отрезок находится внутри бесконечной усеченной пирамиды, а следовательно полностью невидим (Рис. Затенение отрезка плоскостью при перспективной проекции -73).

Для того чтобы определить наличие этого случая, можно использовать результаты анализов, выполняемого для предыдущих случая. Если окажется,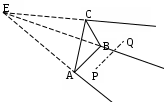



Рис. Затенение отрезка плоскостью при перспективной проекции ‑73
что заданный отрезок находится с внутренней стороны относительно всех граней бесконечной усеченной пирамиды, то отрезок полностью невидим.