Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР. 1 отображение просранства пользователя и машинного носителя 4

• Название: 1 отображение просранства пользователя и машинного носителя 4
• Дата: 24.09.2022
• Размер: 1.86 Mb.
• Имя файла: Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР.doc
• Тип: Документы; #693275
• страница: 19 из 20

6.8 Удаление затеняемых ребер в аксонометрической проекции

Рассмотрим процедуру удаления невидимых ребер при аксонометрической проекции для конкретного объекта, приведенного на Рис. Удаление затеняемых ребер в аксонометрической проекции-77.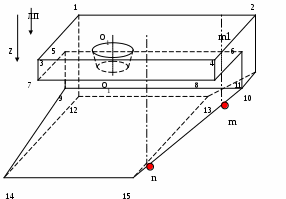




Рис. Удаление затеняемых ребер в аксонометрической проекции‑77
На рисунке приняты следующие обозначения:

• 
  Z – координатная ось видовой системы;
  
• 
  лп – направленность линий проецирования (параллельно оси Z);
  
• 
  О₁, О₂ - ось конической поверхности;
  
• 
  цифрами обозначены все узловые точки, определяющие объект проецирования.
  

Сначала строится проволочная модель проецируемого объекта, которая будет иметь вид, приведенный на Рис. Удаление затеняемых ребер в аксонометрической проекции-78.

На рисунке отсутствуют очерки конической проекции, так как ее ось параллельна линиям проецирования. В результате коническая поверхность на плоскости проекции оказалось представлена только своими ребрами, которыми являются две окружности.

Далее по выше описанной методике определяются явно невидимые ребра.

Для заданного объекта единственным явно невидимым ребром будет ребро, определяемое узловыми точками 13, 15.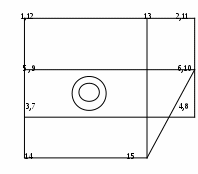


Рис. Удаление затеняемых ребер в аксонометрической проекции‑78
После его удаления проволочная модель примет вид, приведенный на а).

Для оставшихся ребер необходимо решить задачу их затенения гранями переднего плана. Один из подходов при решении этой задачи, основан на использовании принципа конкурирующих точек.

Проекция объекта, полученная после отбрасывания всех явно невидимых ребер, рассматривается как граф. Вершинами этого графа являются узловые точки, отображенные на проекции. Кроме того, в качестве вершин графа также используются точки пересечения ребер на проекции. В качестве дуг графа рассматриваются проекции ребер или их частей.

Очевидно, что дуга графа видима на плоскости проекции, если видима хотя бы одна ее внутренняя точка.

При определении видимости дуги используется принцип конкурирующих точек, который заключается в следующем.

Для определения видимости некоторой точки, в видовой системе координат через нее проводится линия, параллельная оси Z_в, и находятся точки пересечения этой линии со всеми гранями проецируемого объекта. Если хотя бы одна из найденных точек пересечения будет иметь координату Z_в, меньшую, чем у анализируемой точки, то это означает, что анализируемая точка на плоскости проекции затенена соответствующей гранью, а, следовательно, она не видна. В противном случае, анализируемая точка имеет минимальную координату по оси Z_в и ребро, которой она принадлежит, затеняет все другие точки, т.е. анализируемая точка видима.

Для рассматриваемого объекта граф будет иметь вид, приведенный на b). Помимо вершин, соответствующих проекциям узловых точек, дополнительно присутствует вершина f, соответствующая пересечению проекций ребер.

Для приведенного графа определим видимость дуги fd. С этой целью возьмем одну из ее внутренних точек m_п, в видовой системе координат найдем ей соответствующую точку m и проведем через нее линию m1 m,


a b

c d


m_п

e f h
n_п

а) i k b)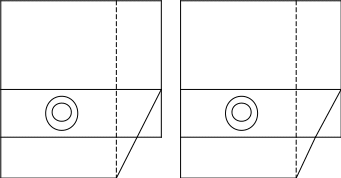








a) b)


Рис. Удаление затеняемых ребер в аксонометрической проекции‑79
параллельную координатной оси Z_в (Рис. Удаление затеняемых ребер в аксонометрической проекции-77). Прямая m1 m2 пересекает три грани исходного объекта, заданные узловыми точками 1,3,4,2; 5,6,8,7; 13,10,11,15. Среди полученных точек пересечения этих граней с линией m1m2 точка пересечения с гранью, заданной узловыми точками 1,3,4,2, будет иметь координату по оси Z_в меньшую, чем анализируемая точка, а следовательно, точка m затенена этой гранью, а, следовательно, ребро fd на плоскости проекции не видимо.

Определим видимость дуги fk графа b). Для этого возьмем одну из ее внутренних точек n_п, в видовой системе координат найдем ей соответствующую точку «n» и проведем через нее линию п1 n, параллельную координатной оси Z_в (Рис. Удаление затеняемых ребер в аксонометрической проекции-77). Прямая n1 n не пересекает ни одной грани, а следовательно точка n ничем не затеняется, поэтому она видна, а, следовательно, дуга f k должна быть отображена на плоскости проекции.

1,12 13 2,11
5 , 9 6,10
3,7 4,8

14 15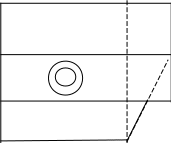



Рис. Удаление затеняемых ребер в аксонометрической проекции‑80
Аналогичные действия выполняются для всех дуг графа. В результате для заданного объекта будет получена проекция, приведенная на Error: Reference source not found.