Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР. 1 отображение просранства пользователя и машинного носителя 4

• Название: 1 отображение просранства пользователя и машинного носителя 4
• Дата: 24.09.2022
• Размер: 1.86 Mb.
• Имя файла: Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР.doc
• Тип: Документы; #693275
• страница: 18 из 20

6.7 Очерки

При задания для проецировании объекта с криволинейными гранями, помимо определения множество точек, ребер и граней объекта проецирования, необходимо определить множество очерков для его криволинейных граней.

Очерки криволинейной поверхности представляют собой линии на этой криволинейной поверхности, разделяющие эту поверхность на части, которые не видимы, и части, которые видны на плоскости проекции. В данном случае речь идет о проекции только рассматриваемой криволинейной поверхности и не учитывается возможное затенение этой поверхности другими поверхностями переднего плана.

Части, на которые очерки разбивается криволинейную поверхность, называются отсеками.

Положение очерков криволинейных граней определяется параметрами проекции, поэтому очерки должны определяться после того, как совершен переход в видовую систему координат.

Определение очерка криволинейной поверхности, в общем случае, представляет собой сравнительно сложную задачу. Поэтому, как правило, заданную криволинейную поверхность аппроксимируют с помощью одной из типовых криволинейных поверхностей, к числу которых относятся:

• 
  цилиндрическая поверхность;
  
• 
  сферическая поверхность;
  
• 
  коническая поверхность.
  

Рассмотрим нахождение очерков для этих видов криволинейных поверхностей.

Нахождение очерков сферической поверхности иллюстрируется Error: Reference source not found.

На рисунке приняты следующие обозначения:

• 
  О - центр сферы;
  
• 
  О_п – проекция центра сферы;
  
• 
  ГМ – главный меридиан заданной сферы;
  
• 
  Пл1- плоскость, проходящая через центр сферы, параллельная плоскости проекции;
  

• 
  X_в, Y_в, Z_в – координатные оси видовой системы координат;
  
• 
  X_п, Y_п – координатные оси на плоскости проекции.
  

Чтобы найти очерк на поверхности сферы необходимо через центр сферы провести плоскость (пл1 на Error: Reference source not found), параллельную плоскости проекции. Линия пересечения этой поверхности и сферы, имеющая форму окружности, называется главным меридианом (ГМ) сферической поверхности. Этот главный меридиан и является искомым очерком.

Проекцией этого очерка будет являться окружность с тем же радиусом. Центром этой окружности является проекция центр исходной сферы на плоскость проекции (О_п на Рис. Очерки-74).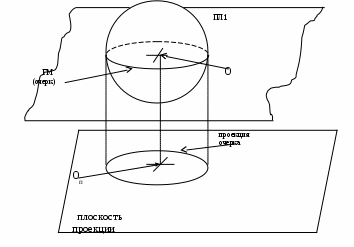



Рис. Очерки‑74
Для определения очерка цилиндрической поверхности, через ось заданного цилиндра o₁o₂ (Рис. Очерки-75) проводится плоскость Пл1, перпендикулярная плоскости проекции. Далее через ось цилиндра проводится плоскость Пл2, перпендикулярная плоскости Пл1. Ее пересечения с цилиндрической поверхности образуют две прямые линии oч₁оч₂ и oч₃oч₄, которые являются очерками цилиндрической поверхности. Проекцией этих очерков являются прямые линии oч_1поч_2п и oч_3пoч_4п, показанные на Рис. Очерки-75 .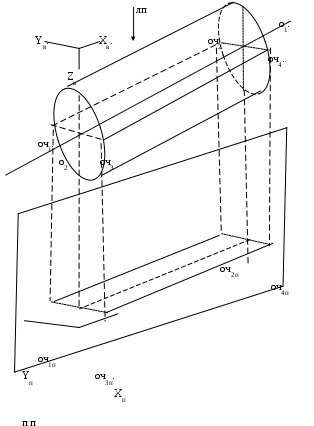




Рис. Очерки‑75

Построение очерков конической поверхности иллюстрируется Рис. Очерки-76.

На приведенном рисунке приняты следующие обозначения:

• 
  O - вершина конуса;
  
• 
  OO₁- ось конуса;
  
• 
  X_в, Y_в, Z_в – видовая система координат;
  
• 
  ПП – плоскость проекции;
  
• 
  X_п, Y_п, –система координат плоскости проекции;
  
• 
  лп – линии проекции;
  
• 
  O₁- центр сферы, вписанной в конус;
  
• 
  O₂ – окружность-касательная вписанной сферы, имеющая центр в точке O₁, и исходной конической поверхности;
  
• 
  Oч₁, Oч₁ – точки, лежащие на очерках конической поверхности;
  

Oч_1п, Oч_1п - точки, через которые проходят линии, соответствующие проекциям очерков конической поверхности.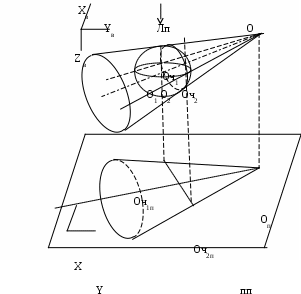


Рис. Очерки‑76

Коническая поверхность имеет два очерка в виде прямых линий. Очевидно, что эти линии проходят через вершин конуса - точку О. Для однозначного задания очерка поэтому необходимо найти по одной точке для каждого очерка.

Для построения очерков конической поверхности выполняют следующие действия.

В заданную коническую поверхность вписывается сфера (например, с центром в точке О₁) и определяется касательная этой сферы с конической поверхностью. В рассматриваемом на рисунке случае линия касания будет иметь форму окружности с центром в точке О₂, лежащей на оси конуса.

Очевидно, что из всех точек сферической поверхности точками, принадлежащими очеркам, могут быть только точки, принадлежащие окружности-касательной. С другой стороны, эти точки обязательно должна находиться на окружности главного меридиана вписанной сферы.

Поэтому искомыми точками будет точки пересечения окружности главного меридиана вписанной сферы и окружности-касательной. Эти точки можно определить как точки пересечения окружности-касательной и плоскости, проходящей через центр вписанной сферы O₁, параллельной плоскости проекции. Такими точками на приведенном рисунке являются Oч₁и Oч₂.

Для построения проекций очерков достаточно найти точки Oч_1п и Oч_2п, являющихся проекциями найденных точек Oч₁и Oч₂ на плоскость проекции, и, используя эти точки и точку O_п проекции вершины конуса, построить две прямые линии, соответствующие проекциям очерков заданной конической поверхности (см. Рис. Очерки-76).