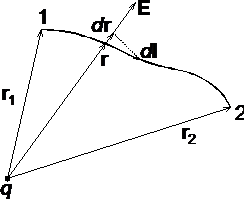1. Предмет і метод фізики та її зв'язок з суміжними науками

• Название: 1. Предмет і метод фізики та її зв'язок з суміжними науками
• Анкор: Shpori.docx
• Дата: 11.08.2018
• Размер: 1.26 Mb.
• Имя файла: Shpori.docx
• Тип: Документы; #22815
• страница: 7 из 8

р  = lq,

де l – вектор, направлений від від’ємного заряду до додатнього.
Диполь може слугувати електричною моделлю багатьох молекул.
Електричним дипольним моментом володіє, наприклад, нейтральна молекула води (H₂O), так як центри двох атомів водню розташовані не на одній прямі з центром атома кисню, а під кутом 105° (мал. 4). Дипольний момент молекули води p = 6,2·10^–30 Кл · м.

 

В багатьох задачах електростатики потрібно за заданим разподілом зарядів визначити електричне полеЕ. Нехай, наприклад, потрібно знайти електричне поле довгої однорідно зарядженої нитки (мал. 5) на віддалі R від неї.

 

Поле в точці спостереження P можна представити як суперпозицію кулонівських полів, які створюють малі елементи Δx нитки, з зарядом τΔx, де τ – заряд нитки на одиницю довжини. Задача зводиться до сумування (інтегрування) елементарних полів ΔЕ. Результуюче поле  дорівнює:

Е = τ/2πε₀∙R.
Вектор Е всюди напрямлений вздовж  радіуса R.  Це випливає з симетрії задачі. Вже цей простий приклад показує, що прямий шлях визначення поля за заданим розподілом зарядів приводить до громіздких математичних розрахунків. В деяких випадках можна значно спростити розрахунки, якщо скористатись теоремою Гауса, яка виражає фундаментальні властивості електричного поля.

52.Теорема Гауса,напруженість електричного поля, рівномірно зарядженої сферичної поверхні.

Теорема Гауса - один із основних законів електростатики, еквівалентний закону Кулона, твердження про зв'язок між потоком вектора електричної індукції через замкнену поверхню, і сумарним зарядом, в об'ємі, оточеному цією поверхнею. Теорема Гауса справедлива також для змінних полів і є одним із основних законів електродинаміки.

В системі СІ теорема Гауса має вигляд:

,

де D - вектор електричної індукції,  - сумарний електричний заряд в об'ємі, оточеному поверхнею S:



де  - густина заряду.

В гаусовій системі одиниць СГСГ теорема Гауса формулюється

,

де  - напруженість електричного поля.

Поле зарядженої кулі

У просторі, який оточує заряджену кулю, візьмемо довільну точку /, віддалену від центра кулі на відстань г (рис. 7.6, а). Виділимо сферичну поверхню, концентричну з поверхнею зарядженої кулі, так, щоб точка / лежала на цій поверхні. Внаслідок симетрії всі точки виділеної поверхні мають однакову напруженість. При цьому вектор напруженості Е напрямлений радіально у кожній точці, тобто перпендикулярно до вибраної сферичної поверхні.

Потік вектора напруженості поля  крізь виділену сферичну поверхню



Заряд кулі



де а — поверхнева густина заряду; R — радіус кулі. Згідно з теоремою Гауса [див. формулу (7.8)],



Звідси для напруженості поля дістанемо вираз



Напруженість поля зарядженої кулі має такий самий вираз, який випливає із закону Кулона для точкового зарядженого тіла. Отже, заряд кулі можна вважати зосередженим в центрі і розглядати заряджену кулю як точкове заряджене тіло. При г = /?



На рис. 7.6, а подано графіки залежності напруженості і потенціалу поля відокремленої зарядженої кулі від відстані г.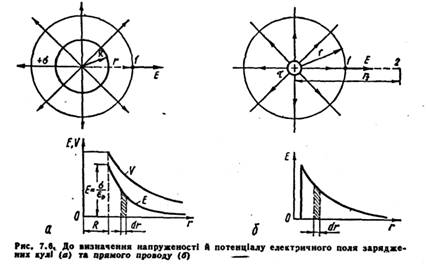



Поле зарядженого прямого проводу

Проведемо через деяку точку 1 простору циліндричну поверхню, вісь якої збігається з віссю проводу круглого перерізу (рис. 7.6, б).

Внаслідок симетрії у всіх точках виділеної поверхні лінії напруженості перпендикулярні до неї, а напруженість поля однакова: £„ = £'.

Потік вектора напруженості



де 2лг/ — бічна поверхня циліндра.

Потік через основи циліндра дорівнює нулеві, оскільки лінії напруженості не пронизують їх.



де Q •• т/, а т — лІніАна густина заряду на проводі.

Згідно з теоремою Гауса,

 

53.Теорема Гауса,напруженість електричного поля, об’ємно зарядженої кулі.

Поле об'ємно зарядженої кулі

Куля радіусу R із загальним зарядом заряджена рівномірно з об'ємною густиною (– заряд, що припадає на одиницю об'єму). Внаслідок симетрії для напруженості поля ззовні кулі матимемо той же результат, що і у разі сферичної поверхні:

.

 

Усередині кулі напруженість інша. Сфера радіусу '< R охоплює заряд .

Тому, згідно з теоремою Остроградського-Гаусса,

.

Враховуючи, що

,

отримаємо



54.Робота сил електростатичного поля над зарядом. Потенціальна енергія заряду в полі.

На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила 
F= q E. При перемещении заряда на отрезке dl силами поля совершается работа

dA = F dl=q E dl cos (E, dl).

При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна

 .

Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого 

 .

Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl).

Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом: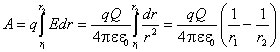



Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении.

Для электрического поля, созданного системой зарядов Q₁, Q₂,, Q_n, работа перемещения заряда q равна алгебраической сумме работ составляющих сил: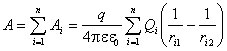

 .

Таким же образом, как и каждая из составляющих работ, суммарная работа зависит только от начального и конечного положений заряда q.

Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичногоположительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:



Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.

 .

Равенство нулю означает, что силы электрического поля являются силамиконсервативными, а само поле - потенциальным.

Робота при переміщенні заряду  з точки 1 в точку 2 дорівнює:



Ця робота не залежить від траєкторії переміщення, а визначається лише початковим (1) і кінцевим (2) положенням заряду. Отже, електростатичне поле точкового заряду є потенціальним, а електростатичні сили – консервативними.

Оскільки робота консервативних сил виконується за рахунок зменшення по- тенціальної енергії, то



Отже, потенціальна енергія заряду  в полі заряду q у вакуумі дорівнює:



Домовимось вважати потенціальну енергію заряду  такою, що дорівнює нулю на нескінченно великій відстані від q. При r і . Тому потенціальна енергія заряду , що перебуває на відстані r від точкового заряду q, дорівнює

.

Якщо заряди та q однойменні, то потенціальна енергія їхньої взаємодії (відштовхування) додатна і зростає при зближенні цих зарядів (рис. 74). У випадку взаємного притягання різнойменних зарядів потенціальна енергія їхньої взаємодії від’ємна і зменшується при наближенні одного із зарядів до іншого.

Потенціальна енергія  заряду  що перебуває в полі точкових зарядів , дорівнює сумі його потенціальних енергій  у полях, що створюються кожним зарядом зокрема:

,

де відстань від заряду  до заряду .

55. Діелектрики . Полярні і неполярні молекули. Поляризація діелектриків.

Діелектриками (або ізоляторами) називаються речовини, які не здатні проводити електричний струм.

У природі ідеальних ізоляторів не існує, вони проводять струм в  разів гірше ніж провідники.

Питомий опір діелектриків становить  Ом. У діелектриках немає вільних електричних зарядів (електронів), як у металах або інших провідниках.

Кожна молекула (або атом) діелектрика має позитивно заряджені ядра і негативно заряджені електрони, які рухаються навколо ядер. Позитивні заряди всіх ядер дорівнюють абсолютній величині заряду всіх електронів, а тому молекула речовини загалом електрично нейтральна.

Вивчаючи електричні властивості діелектриків, молекули діелектриків можна зобразити як систему, що складається з двох точкових зарядів.

Замінимо всі позитивні заряди ядер молекули одним сумарним зарядом +q, що перебуває в центрі мас позитивних зарядів, а всі негативні заряди – одним сумарним негативним зарядом-q, що перебуває в центрі маси негативних зарядів. Тоді молекулу діелектрика можна розглядати як диполь, який складається із зарядів +q i -q.

Діелектрики поділяються на три типи.

І.Неполярні діелектрики – це діелектрики, які складаються з молекул, центри мас позитивних і негативних зарядів яких збігаються за відсутності електричного поля (рис. 78).

Прикладом неполярних діелектриків є гази . Молекули таких діелектриків називаються неполярними. Дипольний момент таких молекул за відсутності зовнішнього електричного поля дорівнює нулю.
IІ. Полярні діелектрики – це діелектрики, в яких центри мас позитивних і негативних зарядів не збігаються, тобто мають асиметричну будову (рис. 79).

До полярних діелектриків належать гази , ,  та ін., рідини – вода , соляна кислота , бензол  тощо.
Молекули таких діелектриків називають полярними. Ці молекули за відсутності зовнішнього поля мають дипольні моменти . Їх називають жорсткими диполями.

ІІІ. Іонні діелектрики – це речовини, молекули яких мають іонну будову. Прикладом таких діелектриків є   та інші.

Іонні кристали є просторовими ґратками з правильним чергуванням іонів різних знаків (рис. 80). У цих кристалах не можна виділити окремі молекули. Іонні кристали необхідно розглядати як систему вміщених одна в одну іонних підґраток. У цих діелектриках кожна пара сусідніх різноіменних іонів подібна до диполя.




Розглянемо, що відбувається з діелектриками при внесенні їх в однорідне електричне поле.

І. Неполярні діелектрики. Електронна поляризація

Сили, з якими електричне поле діє на позитивні і негативні заряди молекул, напрямлені протилежно і тому розсувають їх. В електричному полі центри мас позитивних і негативних зарядів кожної молекули не збігаються, а зміщенні на відстань між ними (рис. 81). Чим більша напруженість поля , тим на більшу відстань розсуваються заряди протилежних знаків. Молекула з неполярної перетворюється в полярну з дипольним моментом .
Оскільки , а , то , або , де – електрична стала,  поляризованість окремої молекули діелектрика. Величина  має неоднакові значення для атомів і молекул різних речовин. Поляризованість  характеризує здатність електронів в атомі або в молекулі зміщуватись під дією сил електричного поля.

Дипольні моменти  молекул неполяризованих діелектриків називають індукованими, або квазіпружними.

При внесенні неполярного діелектрика в електричне поле всі індуковані дипольні моменти розміщуються ланцюжками вздовж ліній напруженості  (рис. 82), де – негативні заряди, а – позитивні. Внаслідок цього грані діелектрика набувають різноіменних зарядів – діелектрик поляризується. Такого роду поляризація діелектрика називається електронною.