1. Предмет і метод фізики та її зв'язок з суміжними науками

• Название: 1. Предмет і метод фізики та її зв'язок з суміжними науками
• Анкор: Shpori.docx
• Дата: 11.08.2018
• Размер: 1.26 Mb.
• Имя файла: Shpori.docx
• Тип: Документы; #22815
• страница: 8 из 8

II. Полярні діелектрики. Дипольна, або орієнтаційна поляризація

Якщо діелектрик з полярними молекулами не перебуває у зовнішньому електричному полі, то внаслідок хаотичного теплового руху молекул вектори їхніх дипольних моментів орієнтовані хаотично (рис. 83). Tому векторна сума дипольних моментів всіх молекул, які перебувають у довільному об'ємі  діелектрика, дорів- нює нулю.

Якщо діелектрик з полярними молекулами внести в електричне поле, то під дією поля полярні молекули діелектрика намагаються повернутись так, щоб вектори їх дипольних моментів збігалися з напрямком вектора напруженості поля  (рис. 84).




Але тепловий рух молекул хаотично розкидає диполі і заважає орієнтації всіх векторів  (дипольних моментів) вздовж поля. Внаслідок спільної дії цих двох факторів в діелектрику переважає орієнтація дипольних моментів молекул вздовж поля. Ця орієнтація буде тим повнішою, чим сильніше електричне поле в діелектрика і чим слабший тепловий рух молекул, тобто, чим нижча температура. Цей процес називають орієнтаційною поляризацією діелектрика.

III. Іонні діелектрики. Іонна поляризація

У кристалічних діелектриках, які мають кубічні кристалічні ґратки ( та інші) під дією електричного поля всі позитивні іони зміщуються в напрямку напруженості поля , а всі негативні іони – в протилежному напрямку (рис. 85).
При цьому в кожній одиниці об'єму кристала перебуває однакова кількість позитивних і негативних іонів, а на кожній з двох протилежних граней кристала, перпендикулярних до вектора напруженості електричного поля, містяться іони якого-небудь одного знака. Такий вид поляризації називають іонною поляризацією.

Заряди, які виникають на гранях діелекрика, не вільні, вони зв’язані з атомами та молекулами речовини.

Явище обмеженого зміщення зарядів в атомах і молекулах або напрямленої орієнтації дипольних моментів жорстких молекул в зовнішньому електричному полі, внаслідок якого на поверхні діелектрика виникають зв’язані електричні заряди, називається поляризацією діелектриків.

Ступінь поляризації діелектрика характеризується вектором поляризації, або поляризованістю.

Вектором поляризації називають границю відношення електричного моменту деякого об'єму діелектрика до цього об'єму, коли об'єм прямує до нуля:

,

де  – дипольний момент і-го диполя, n – кількість диполів, які знаходяться в об'ємі .

Отже, вектор  є дипольним моментом одиниці об'єму діелектрика, який виникає при його поляризації.

Для однорідного діелектрика, який перебуває в однорідному електричному полі, справедлива рівність: , де n – кількість молекул в одиниці об'єму,  – дипольний момент молекули. Оскільки , то .

Позначимо , отже, . Коефіцієнт  називається діелектричною сприйнятливістю речовини або поляризованістю одиниці об'єму діелектрика.  – величина безрозмірна ( для води, для спиртів).

 56. Провідники в електричному полі.

Характерною особливістю провідників є наявність у них вільних носіїв заряду. Якщо провідник поміщають у зовнішнє електростатичне поле , то кожен вільний заряд діє сила  (рис. 87). Під дією сили  відбувається переміщення вільних носіїв заряду і внаслідок цього відбувається перерозподіл електричних зарядів: на одній грані провідника буде надлишок вільних електронів, які заряджають її негативно, на іншій виникає нестача їх і ця грань заряджається позитивно.
Явище перерозподілу вільних носіїв заряду у провіднику під дією зовнішнього електричного поля, внаслідок чого виникає електризація, називається електростатичною індукцією, або електризацією через вплив.

Індуковані на гранях заряди створюють всередині провідника внутрішнє електростатичне поле , яке діє на вільні електрони із силою . Переміщення вільних зарядів у провіднику припиняється, коли . Тоді

.

Оскільки , то

, .

Внутрішнє поле дорівнює за величиною і протилежне за напрямком зовнішньому. Результуюча напруженість поля всередині провідника дорівнює нулю.

Відсутність поля всередині провідника означає, згідно з , що потенціал у всіх точках всередині провідника постійний (), тобто поверхня провідника в електростатичному полі є еквіпотенціальною.

Звідси вектор напруженості поля на зовнішній поверхні провідника спрямований по нормалі до кожної точки її поверхні.

Якщо провіднику надати деякий заряд q, то нескомпенсовані заряди розміщуються лише на поверхні провідника.

Знайдемо взаємозв’язок між напруженістю Е поля поблизу поверхні зарядженого провідника і поверхневою густиною  зарядів на її поверхні.

Для цього розглянемо замкнену поверхню у вигляді циліндра з основою , вісь якого орієнтована вздовж вектора  (рис. 88), і застосуємо теорему Остроградського – Ґаусса.



Оскільки поле всередині провідника відсутнє, потік  через замкнену циліндричну поверхню визначається лише потоком через зовнішню основу циліндра:

.

Звідси

,

або

,

де  відносна діелектрична проникність середовища, в якому знаходиться провідник.

Це співвідношення визначає напруженість електричного поля поблизу поверхні провідника довільної форми.

Дослідження розподілу зарядів на провідниках довільної форми можна провести за допомогою сітки Кольбе – гнучкої металевої сітки, до якої по обидві сторони приклеєні легкі паперові смужки. Вона встановлюється на ізолюючих підставках, а сітці надається певний заряд.

Кут відхилення паперових смужок на сітці залежить від величини заряду. На прямій сітці всі смужки відхиляються на однаковий кут, що свідчить про рівномірний розподіл заряду на поверхні площини сітки.

При наданні сітці форми циліндра відхиляються тільки ті смужки, які розміщені на зовнішній поверхні циліндра. Якщо ж різні ділянки сітки мають неоднакову кривину, то кут відхилення смужок також буде різним. Це означає, що поверхнева густина заряду на різних ділянках тіла довільної форми неоднакова.

Нейтральний провідник, внесений в електростатичне поле, розриває частину ліній напруженості; вони закінчуються на від’ємних індукованих зарядах і знову починаються на додатних (рис. 89).



Лінії напруженості електричного поля перпендикулярні до поверхні провідника, оскільки при такій умові індуковані заряди не будуть рухатися вздовж поверхні провідника.

У стані рівноваги всередині провідника заряди відсутні, тому створення всередині нього порожнини не впливає на конфігурацію розміщення зарядів і тим самим на електростатичне поле. Всередині порожнини поле відсутнє. На цьому ґрунтується електростатичний захист – екранування тіл від впливу зовнішніх електростатичних полів.

 

57. Електростатичне поле в діалектриках

Помістимо діелектрик в однорідне електричне поле (між двома металевими пластинами). З боку електричного поля на диполь буде діяти сила, яка прагне розвернути диполь вздовж силових ліній поля.

Біля додатньої пластини на поверхні діелектрика виникають від”ємні заряди диполів, а біля від”ємної – додатні. Тому на поверхні діелектрика виникає зв”язаний заряд. В об”ємі зв”язаний заряд рівний нулю.

В неполярному діелектрику під дією поля молекули деформуються і їх можна розглядати як пружні електричні диполі.

Отже, діелектрик, вміщений в електричне поле, поляризується.

Електричне поле поляризаційних зарядів завжди спрямоване назустріч зовнішньому полю, тому зовнішнє поле всередині діелектрика послаблюється (але не компенсується повністю, як у провідниках), а поблизу діелектрика поле спотворюється.


Зв”язаний заряд створює в діелектрику електричне поле Е1, що спрямоване проти напруженості зовнішнього поля зарядів на пластинах Е0. Через це поле всередині діелектрика послаблюється. Напруженість результуючого поля становить: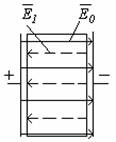

Е = Е0 – Е1.

Для характеристики електричних властивостей діелектрика вводять фізичну величину – діелектричну проникливість.

Діелектрична проникливість середовища – це фізична величина, що показує, у скільки разів модуль напруженості електричного поля Е всередині діелектрика менший за модуль напруженості поля Е0 у вакуумі:

Напруженість електричного поля точкового заряду або зарядженої кулі, які вміщені в однорідний діелектрик:

Закон Кулона для зарядів в однорідному діелектрику:

58. Електроємність. Конденсатори та їх ємність. З’єднання конденсаторів

Ємністю одного зарядженого провідника називають величину

У випадку двох провідників 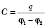(вимірюється у Фарадах)

Ємність одного провідника мала. Для збільшення ємності провідника до нього наближають інший провідник, а між ними розташовують діелектрик. Така система називається конденсатором(накопичувачем).
Існують конденсатори з обкладками різної геометричної форми (плоскі, сферичні, циліндричні). Формула ємності плоского конденсатора

де S — площа однієї пластини, d — відстань між пластинами.
Часто використовують не окремі конденсатори, а кілька з’єднаних між собою.
1) Паралельне з’єднання конденсаторів дозволяє одержати великі ємності: . ,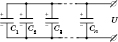



2) Послідовне з’єднання: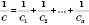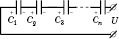

, , .




59. Енергія зарядженого конденсатора. Енергія електростатичного поля.

Нехай є відокремлений провідник, заряд, ємність і потенціал якого становлять, відповідно, q, C, . Збільшимо заряд цього провідника на dq. Для цього треба перенести заряд dq з нескінченності до поверхні провідника, затративши на це роботу

, .

Щоб зарядити тіло від нульового потенціалу до , треба виконати роботу

.

Енергія зарядженого провідника числово дорівнює тій роботі, яку треба виконати, щоб зарядити цей провідник, тобто

.

Під час зарядження конденсатора витрачається робота із перенесення електричних зарядів з однієї обкладки на іншу. Енергію зарядженого конденсатора визначають за формулою:

,

де  – різниця потенціалів між обкладками.

Знайдемо енергію електричного поля.



де V = Sd – об’єм конденсатора.

Відомо, що .

Тоді

.

Ці формули показують, що енергія конденсатора виражається через величину, що характеризує електростатичне поле, – через напруженість Е. Це означає, що електростатичне поле володіє енергією і можна говорити про енергію електростатичного поля. Енергія є однією з характеристик стану матерії. Тому енергія нерозривно пов’язана з її матеріальним носієм – електричним полем. Енергія електричного поля локалізована у просторі, де існує це поле.

Вираз  відповідає положенням теорії далекодії, де W розглядається як потенціальна енергія заряджених тіл, що притягуються або відштовхуються один від одного. Формула  відповідає уявленням теорії поля (теорії близькодії), де вважається, що енергія, подібно до речовини, розподілена у просторі з об’ємною густиною

.

Енергія  нескінченно малого об’єму dV поля дорівнює:

.

Інтегруючи це рівняння по всьому об’єму  поля, знаходимо повну енергію  електростатичного поля:

.