1. Предмет і метод фізики та її зв'язок з суміжними науками
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
3. Крива розподілу швидкостей не є симетрична - в один бік спад кривої крутіший, ніж в другий. 4. На розподіл молекулярних швидкостей дуже сильно впливає температура: з підвищенням температури максимум на кривій розподілу зміщується вздовж осі абсцис вправо. 5. Криві розподілу молекул за швидкостями для різних газів мають однаковий характер, хоча їх координати і положення максимумів різні, оскільки швидкості молекул залежать не лише від температури, а й від маси. Найбільшймовірна швидкість хаотичного руху молекул відповідає максимуму функції розподілу: 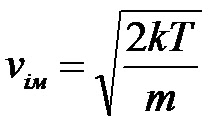 Формула Максвелла також дає змогу визначити середню арифметичну швидкість молекул: 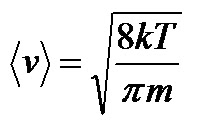 Для середньої квадратичної швидкості розподіл Максвела дає наступний вираз: 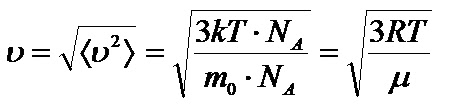 Уперше швидкість теплового руху атомів експериментально визначив німецький вчений-фізик Отто Штерн 1920 року. Результати експерименту повністю узгоджувалися із теорією роподілу Максвела, тим самим підтверджуючи її правильність. 45.Закон розподілу Максвела – Больцмана. У відсутність силових полів концентрація молекули газу всюди однакова. Якщо з’являється силове поле, то концентрація молекул газу від точки до точки змінюється, але (!) швидкості молекул газу в кожній точці простору розподіленні за законом Максвела. Тоді кількість частинок в об’ємі  визначиться з допомогою формули Больцмана визначиться з допомогою формули Больцмана , ,а кількість частинок з них, що мають швидкість в межах швидкісного інтервалу 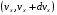 , ,  та та  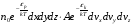 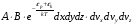 - формула Максвела-Больцмана. Дане рівняння дає відносну кількість частинок, які, маючи потенціальну енергію 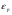 , знаходяться в об’ємі , знаходяться в об’ємі  біля точки біля точки 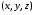 і одночасно мають швидкості в швидкісному об’єму і одночасно мають швидкості в швидкісному об’єму 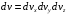 поблизу швидкості поблизу швидкості  . Тобто ця формула визначає відносну кількість частинок в 6-мірному просторі в об’ємі . Тобто ця формула визначає відносну кількість частинок в 6-мірному просторі в об’ємі 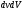 біля точки біля точки 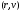 . .
Коли молекули підіймаються вгору, з їхнього потоку вибиваються найбільш повільні, тобто „холодні” молекули. І розрахунок середньої енергії ведеться за малою кількістю частинок, але за більш „гарячими” з них. При русі вниз, навпаки, частинки прискорюються, але водночас пучок поповнюються більш повільними, „холодними” молекулами. Тобто середня швидкість молекул залишається незмінною. Іще раз, сила тяжіння змінює лише концентрацію частинок, але не температуру. Лоренц приводив такий приклад: є два міста А і В. Кількість мешканців певного віку в місті А дорівнює подвоєній кількості мешканців того ж віку в місті В. Зрозуміло, що середній вік мешканців міст А і В однаковий. Дослід Перрена. Перрен використав той факт, що, невеличкі зважені частинки можна розглядати як невзаємодіючі молекули великих розмірів. Тому можна очікувати, що „макромолекули” зважені у рідині, в полі сил тяжіння будуть розподіленні за висотою як і молекули газу, тобто за законом Больцмана. Але маси великих частинок великі, і їх концентрація з висотою буде швидко убивати, так що ми отримаємо стан, в якому частинки лежать на дні посудини. Для того, щоб важкі частинки не „осіли” на дно, а розподілилися у достатньо товстому шарі за висотою, необхідно їх розмістити у рідині, густина якої  лише трохи менша за густину частинок лише трохи менша за густину частинок  . Тоді потенціальна енергія частинок в результаті дії сили Архімеда буде достатньо малою: . Тоді потенціальна енергія частинок в результаті дії сили Архімеда буде достатньо малою: . (8) . (8)І розподіл концентрації за висотою буде задаватися формулою: 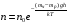 . . 46.Реальні гази. Розглянемо гази за умови, якщо тиск збільшується, а температура зменшується. При цьому зменшується середня довжина вільного пробігу молекули (див. п.4.5), що зумовлює необхідність врахування сил міжмолекулярної взаємодії. Такі умови відповідають стану реального газу. Записати рівняння стану реального газу, урахувавши складні залежності сил взаємодії від відстані, зовсім не просто. У 1873 році голландський вчений Ван дер Ваальс вивів рівняння стану для реального газу. Він узяв за основу рівняння стану ідеального газу і ввів до нього поправки, які враховували наявність сил притягання і сил відштовхування. Сили притягання враховуються додаванням до основного тиску внутрішнього тиску . Цей тиск нібито додатково стискає газ до відповідного об’єму: . Сили відштовхування дуже швидко зростають зі зменшенням відстані між молекулами (див. п.4.9), але вони не можуть зблизитись на відстань, меншу деякого ефективного діаметра молекули (див. п.4.5). Тоді треба врахувати частину об’єму, яку займатимуть самі молекули, причому для руху їм залишається тільки вільний об’єм, що дорівнює різниці реального об’єму і власного об’єму молекул: . За допомогою таких простих, але достатньо логічних міркувань Ван дер Ваальсу вдалося сконструювати рівняння стану реального газу. Для одного моля газу рівняння запишеться так ( – молярний об’єм): 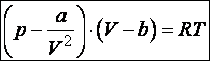 , ,де – константи Ван дер Ваальса. Як виявилось пізніше, значення дорівнює зчетвереному сумарному об’єму всіх молекул, які містяться в одному кіломолі, і для даної речовини є величиною сталою. Зі збільшенням об’єму інші члени в кожній дужці стають настільки малими порівняно з першими членами, що ними можна знехтувати, – і рівняння стану реального газу перетворюється на рівняння ідеального газу. 47. Ізотерми реальних газів. Фазові перетворення. 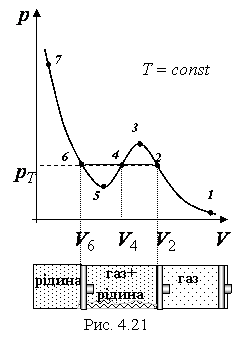 Ізотерми реальних газів, які експериментально отримав Т. Ендрюс відрізняються від ізотерм ідеального газу (див. п.4.7). Розглянемо циліндр з газом, наприклад СО2, і будемо цей газ стискати (рис. 4.21). На рис. 4.21 крива 1-2-4-6-7 відповідає експериментальній ізотермі Ендрюса. Перехід 1→2 визначається звичайною ізотермою Бойля – Маріотта для ідеального газу при значній відстані між молекулами, тобто низькому тиску. Точка 2 ізотерми відповідає стану сухої насиченої пари. Точка 6 відповідає стану насиченої рідини. Перехід 2-4-6 відбувається при незмінному тиску () за даної температури і характеризується тим, що одному значенню тиску відповідає множина об’ємів. Пояснюється це тим, що відбувається конденсація газу, тобто він перетворюється на рідину. Маємо справу з насиченою парою, тиск якої не залежить від температури. Речовина знаходиться у двох агрегатних станах. Починаючи з точки 6 вся пара перетворюється на рідину, а перехід 6→7 відповідає різкому зростанню тиску при незначному збільшенні об’єму, бо на цій ділянці ми вже маємо рідину, а рідина практично не стискається. Повернемось до рівняння Ван дер Ваальса. Якщо розв’язувати його відносно об’єму, то можна отримати рівняння третього степеня, тоді ми будемо мати три корені (наприклад, , та ) для даної ізобари. Крива 1→2→3→4→5→6→7 на рис. 4.21 є теоретичною ізотермою Ван дер Ваальса. Вона відрізняється від експериментальних кривих тим, що передбачила існування так званих метастабільних станів. Перший стан (крива 2→3) відповідає пересиченій парі. Для практичного одержання цієї ділянки треба дуже повільно підвищувати тиск, внаслідок чого вдається затягнути початок конденсації пари аж до точки 3. Другий стан (крива 5→6) відповідає розтягнутій (перегрітій) рідині. Стани пересиченої пари та перегрітої рідини є вкрай нестійкими, тому й називаються метастабільними. Вони руйнуються за найменших зовнішніх впливів, з’являється друга фаза, система прямує до рівноважного стану, і ми потрапляємо на горизонтальну ділянку ізотерми. Зазначимо, що крива 3→4→5 на ізотермі Ван дер Ваальса існувати взагалі не може, оскільки такий процес, коли при сталій температурі одночасно зменшуються тиск та об’єм, є неможливим.  Будемо підвищувати температуру газу і отримаємо сімейство ізотерм Ендрюса (рис. 4.22). Неважко бачити, що з підвищенням температури газу інтервал двофазного стану змен-шується, тобто об’єми насиченої пари і рідини зближуються. Врешті-решт існує така ізотерма, на якій інтервал двофазного стану стягується в точку К (рис. 4.22). Ця температура називається критичною температурою , сама точка – критичною точкою, а тиск і об’єм у цій точці тиском та критичним об’ємом . Стан з параметрами , і називається критичним станом. Критичний стан є станом, при якому співпадають молекулярні характеристики пари та рідини. Наприклад, в критичній точці густина пари дорівнює густині рідини: . Отже, рівняння Ван дер Ваальса передбачило появу критичного стану речовини. Газ, стан якого описується кривою, що знаходиться вище критичної ізотерми, неможливо методом стиснення перетворити в рідину. Для отримання рідини з такого газу необхідно охолодити його до температури, нижчої за критичну. Зазначимо, що пара є газом, який при зменшенні об’єму перетворюється у рідину при будь-якій температурі, а газ є таким агрегатним станом речовини, який перетворюється на рідину тільки при температурі . Наприклад, для гелію = 5 К (-278 оС), для води = 547 К (274 оС). Фазоюназивають однорідну за своїми фізичними властивостями та хімічним складом частину т.д.с. (слід розрізняти фазу і агрегатний стан). Приклади: водяна пара, вода , лід – три різні фази молекулярної сполуки води у різних агрегатних станах – газоподібному, рідкому та твердому. Якщо у рівновазі знаходяться дві або більше фаз, то такий стан називається фазовою рівновагою. Cтан, у якому перебувають у рівновазі тверда, рідка і газоподібна фази речовини, називається потрійною точкою. Перехід речовини з одної фази в іншу називається фазовим переходом, або фазовим перетворенням. Приклади фазового переходів: кипіння - конденсація, кристалізація - плавлення. Через те, що на термодинамічних діаграмах станів („p-v”, „Т-s” та ін.) для реального газу, на відміну від таких же для ідеального газу відображені стани, які відповідають різним фазам, їх ще називають фазовими діаграмами. Правило фаз Гібса Загалом число фаз, що можуть одночасно співіснувати у рівновазі, задається співвідношенням m  n+2, n+2,m – число співіснуючих фаз, n – число компонент у системі. Для однокомпонентної системи (n=1), наприклад води, як ми вже знаємо, m = 3 , тобто у рівновазі, в потрійній точці, одночасно можуть знаходитися три фази. При фазовому переході повинні виконуватися умови механічної та теплової рівноваги фаз, тобто тиск і температура у всіх частинах т.д.с. повинні бути однаковими. Рівноважні процеси ( у т.ч. і фазові переходи) підкоряються принципу Ле – Шательє: якщо на систему, що знаходиться в стані рівноваги, діють зовнішні чинники, що виводять її зі стану рівноваги, то рівновага т.д.с. зміщується у напрямі ослаблення зовнішньої дії. 48. Внутрішня енергія реального газу. Внутрішня енергія реального газу дорівнює сумі кінетичної енергії теплового руху його молекул і потенціальної енергії міжмолекулярної взаємодії. Потенціальна енергія реального газу зумовлена лише силами притягання між молекулами, які приводять до виникнення внутрішнього тиску на газ ![[image]](22815_html_125cd9e3.png) . .Робота, яка затрачається для подолання сил притягання, що діють між молекулами газу, або проти внутрішнього тиску, йде на збільшення потенціальної енергії системи: ![[image]](22815_html_787389fe.png) . .Звідси ![[image]](22815_html_7104aa5f.png) . .Знак “–” означає, що молекулярні сили, які створюють внутрішній тиск , є силами притягання. З достатнім ступенем точності можна вважати, що кінетична енергія для одного моля реального газу дорівнює кінетичній енергії ідеального газу, що перебуває при тій самій температурі. Внутрішня енергія ідеального газу дорівнює тільки кінетичній енергії хаотичного руху молекул. Тому ![[image]](22815_html_4933a982.png) . .Тоді внутрішня енергія одного моля реального газу: і вона зростає із збільшенням температури та об’єму газу. Якщо газ розширюється без теплообміну з навколишнім середовищем міки При адіабатному розширенні без виконання зовнішньої роботи внутрішня енергія газу не міняється. Для ідеального газу означає рівність температур , тобто при адіабатному розширенні ідеального газу у вакуумі його температура не міняється. Для реального газу: ![[image]](22815_html_5d6aa744.png) і і ![[image]](22815_html_63a16383.png) . .З умови отримуємо ![[image]](22815_html_m766d6715.png) . .Оскільки , то , тобто реальний газ при адіабатному розширенні у вакуум охолоджується. При адіабатному стиску реальний газ нагріватиметься. 49. Закон кулона для точкових і не точкових зарядів. Закон Кулона для точкових і неточкових заряджених тіл. Заряджені тіла, розмірами яких можна знехтувати порівняно з відстанню між ними називають точковими зарядженими тілами (зарядами). Про наявність зарядів на тілах можна судити із притягання, відштовхування тіл, яким надано заряди. Здатність електричних зарядів як до взаємного притягання, так і до взаємного відштовхування пояснюється існуванням двох різних видів зарядів. Один вид електричного заряду називають позитивним, а другий – негативним. Тіла, що мають заряди однакового знака, відштовхуються, а тіла із зарядами різних знаків притягуються. За нормальних умов тіла є електронейтральними, тому що заряди всередині них взаємно скомпенсовані, рівномірно розподілені в об’ємі тіла. Процес, що приводить до появи на тілах або різних частинах одного тіла надлишку електричного заряду, називають електризацією. Електризація може відбуватися під дією світла й інших взаємодій, однак внаслідок електризації завжди виконується закон збереження заряду: в ізольованій системі заряджених тіл алгебраїчна сума зарядів – величина стала: 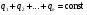 або або 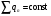 . .Цей закон є фундаментальним законом, як і закон збереження імпульсу, енергії. Справедливість закону збереження заряду підтверджується спостереженнями над величезною кількістю перетворень елементарних частинок. Причина збереження заряду наразі невідома. У природі точкових заряджених тіл не існує, але якщо відстань між тілами набагато більша від їх розмірів, то ні форма, ні розміри заряджених тіл істотно не впливають на взаємодію між ними. У такому разі ці тіла можна вважати точковими. Закон взаємодії точкових заряджених тіл установив 1785 року французький вчений Ш. Кулон. Це основний закон електростатики. Його отримано за допомогою крутильних терезів. Крутильні терези складаються зі скляної палички  , підвішеної на тонкій пружній нитці l. На одному кінці палички закріплено маленьку металеву кульку , підвішеної на тонкій пружній нитці l. На одному кінці палички закріплено маленьку металеву кульку  , на другому – противагу , на другому – противагу 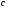 . Ще одну металеву кульку . Ще одну металеву кульку 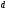 закріплено на кришці терезів нерухомо. закріплено на кришці терезів нерухомо.Якщо кульки зарядити, то в результаті їх взаємодії паличка повертається в горизонтальній площині. За кутом закручування нитки можна визначити силу взаємодії зарядів. Кулон встановив, що сила взаємодії  пропорційна величині зарядів кульок пропорційна величині зарядів кульок  ( ( ) і ) і 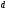 ( ( ) і обернено пропорційна квадрату відстані між ними ) і обернено пропорційна квадрату відстані між ними  : : . .Щоб перейти до рівності, було введено коефіцієнт пропорційності  , що залежить від вибору системи одиниць вимірювання. У СІ , що залежить від вибору системи одиниць вимірювання. У СІ  або або  , ,де 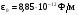 – електрична стала. Остаточно закон Кулона для взаємодії нерухомих точкових заряджених тіл у вакуумі має таку форму запису: – електрична стала. Остаточно закон Кулона для взаємодії нерухомих точкових заряджених тіл у вакуумі має таку форму запису: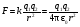 . . Значення  є додатним, тоді різнойменним зарядам відповідає від’ємна сила (притягання), однойменним – додатна сила (відштовхування). є додатним, тоді різнойменним зарядам відповідає від’ємна сила (притягання), однойменним – додатна сила (відштовхування).Таку саму форму має закон всесвітнього тяжіння: замість зарядів у формулу закону тяжіння входять маси, а роль коефіцієнта  відіграє гравітаційна стала відіграє гравітаційна стала 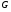 . Сили взаємодії називають центральними. Згідно з третім законом Ньютона . Сили взаємодії називають центральними. Згідно з третім законом Ньютона  (мал. 65). (мал. 65). 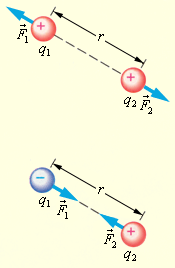 Мал. 65. Кулонівські сили взаємодії Мал. 65. Кулонівські сили взаємодіїУ разі взаємодії різнойменних зарядів (мал. 65), наприклад, 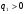 , ,  або або  , , 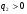 , заряди притягуються. Напрями сил , заряди притягуються. Напрями сил  і і 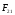 змінюються на протилежні і напрямлені до зарядів. змінюються на протилежні і напрямлені до зарядів.Закон Кулона формулюється так: два нерухомі точкові заряджені тіла взаємодіють із силою, прямо пропорційною добутку цих зарядів і обернено пропорційною квадрату відстані між ними. Сили взаємодії заряджених тіл чисельно рівні між собою і напрямлені вздовж прямої, що з’єднує ці тіла. Згідно із законом Кулона можна розраховувати сили взаємодії тільки нерухомих точкових заряджених тіл. Але будь-яке заряджене тіло можна розглядати як сукупність заряджених матеріальних точок. Тому сила, з якою одне заряджене тіло діє на друге, дорівнює векторній сумі сил, прикладених до всіх точкових зарядів другого тіла з боку кожного точкового заряду першого тіла. Кулон проводив дослідження в повітрі, в якому сила взаємодії зарядів досить точно збігається з силою взаємодії зарядів у вакуумі. Подальші дослідження показали, що наявність речовини навколо заряджених тіл впливає на силу їх взаємодії. Вплив середовища на силу цієї взаємодії можна оцінити, якщо порівняти сили взаємодії між точковими зарядженими тілами у вакуумі ( 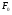 ) і в середовищі ( ) і в середовищі ( ). Назвемо відношення сил ). Назвемо відношення сил  діелектричною проникністю середовища (відносно вакууму) і позначимо його через діелектричною проникністю середовища (відносно вакууму) і позначимо його через 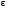 : : . . Із рівняння випливає, що 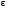 – безрозмірна величина. Таким чином, за наявності непровідного середовища, в яке вміщено заряди, закон Кулона набуде вигляду – безрозмірна величина. Таким чином, за наявності непровідного середовища, в яке вміщено заряди, закон Кулона набуде вигляду . . Для вакууму 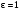 , для гасу , для гасу  , сухого паперу , сухого паперу 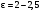 , у дистильованої води , у дистильованої води  . .50. Електростатичне поле в вакуумі, напруженість поля. Електростатичне поле в вакуумі, напруженість поля. Взаємодія зарядів за законом Кулона є експериментально встановленим фактом. Однак математичний вираз закону взаємодії зарядів не розкриває фізичного змісту самого процесу взаємодії, не пояснює, яким чином відбувається дія заряду  на заряд на заряд  . .Теорія близькодії, створена на основі дослідження англійського фізика М. Фарадея, пояснює взаємодію електричних зарядів тим, що навколо кожного електричного заряду існує електричне поле – особливий вид матерії, що існує незалежно від наших знань про нього і має енергію. Електричне поле безперервне в просторі і здатне діяти на інші електричні заряди. Електричне поле — форма матерії, окремий прояв електромагнітного поля; існує навколо нерухомих у вибраній системі відліку електричних зарядів (електростатичне) або виникає в результаті зміни магніт ного поля (вихрове). Електричне поле нерухомих зарядів називають електростатичним. Воно не змінюється з часом. Це поле створюється тільки електричними зарядами. Воно існує в просторі, що оточує ці заряди, і нерозривно з ними пов’язане. Головна властивість електричного поля – здатність діяти на внесені в нього електричні заряди з деякою силою. Тому досліджують електричні поля за допомогою пробного точкового заряду. Пробний заряд 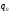 має бути малим, щоб він не спотворював помітно досліджуваного поля. має бути малим, щоб він не спотворював помітно досліджуваного поля. Пробний заряд – позитивно заряджене тіло, поле якого не змінює поле, в яке він внесений. Застосовують для дослідження електричного поля, оскільки головна властивість електричного поля – здатність діяти на внесені в нього електричні заряди з деякою силою. Нехай в точці О знаходиться позитивний точковий заряд  . У довільну точку поля С, створеного зарядом . У довільну точку поля С, створеного зарядом  , і яка знаходиться на відстані , і яка знаходиться на відстані  від цього заряду, помістимо пробний заряд від цього заряду, помістимо пробний заряд 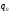 . Модуль сили взаємодії між цими зарядами визначаємо за законом Кулона. . Модуль сили взаємодії між цими зарядами визначаємо за законом Кулона.Поділивши обидві частини формули на 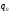 і прирівнявши і прирівнявши  , отримуємо , отримуємо . . Вираз правої частини формули не залежить від заряду 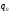 і має стале значення для кожної точки поля, в якій цей заряд знаходиться. Отже, відношення і має стале значення для кожної точки поля, в якій цей заряд знаходиться. Отже, відношення  є також сталим для кожної точки поля. Величину, що виражає це відношення, називають напруженістю електричного поля: є також сталим для кожної точки поля. Величину, що виражає це відношення, називають напруженістю електричного поля: . . Напруженістю електричного поля називають фізичну векторну величину  , що є силовою характеристикою електричного поля в кожній його точці і чисельно дорівнює відношенню сили, з якою поле діє на точковий заряд, поміщений у цю точку, до значення цього заряду. Напрям напруженості збігається з напрямом електричної сили, що діє на пробний позитивний заряд в цій точці: , що є силовою характеристикою електричного поля в кожній його точці і чисельно дорівнює відношенню сили, з якою поле діє на точковий заряд, поміщений у цю точку, до значення цього заряду. Напрям напруженості збігається з напрямом електричної сили, що діє на пробний позитивний заряд в цій точці: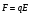 . .51.Електричний диполь. Електричний диполь – це система двох однакових по модулю зарядів різного знака q і –q, росташованих на деякій віддалі l. На мал. 3 зображено картину силових ліній дипольного поля.
Важливою характеристикою електричного диполя є так званий дипольний момент р: |
