1. Предмет і метод фізики та її зв'язок з суміжними науками
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
Дру́гий закон термодина́міки — один із основних законів фізики, закон про неспадання ентропії в ізольованій системі. Він накладає обмеження на кількість корисної роботи, яку може здійснити тепловий двигун. На засадничому рівні другий закон термодинаміки визначає напрямок протікання процесів у фізичній системі - від порядку до безпорядку. Існує багато різних формулювань другого закону термодинаміки, загалом еквівалентних між собою. Неможливо побудувати вічний двигун другого роду. Неможливо передати тепло від холодного тіла до гарячого, не затративши при цьому енергію. Кожна система прагне перейти від порядку до безпорядку. Цикл Карно́ — ідеальний термодинамічний цикл. Цикл складається з чотирьох стадій:
Коефіцієнт корисної дії для двигуна, що працює за циклом Карно, залежить лише від різниці температур нагрівача Tн і охолоджувача Тс. 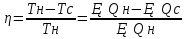 Для збільшення коефіцієнта корисної дії циклу Карно необхідно зробити температуру нагрівача якомога більшою, а температуру охолоджувача — якомога меншою. 39.Нерівність Клаузіуса. Неравенство Клаузиуса (1854): Количество теплоты, полученное системой при любом круговом процессе, делённое на абсолютную температуру, при которой оно было получено (приведённое количество теплоты), неположительно. 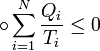 Подведённое количество теплоты, квазистатически полученное системой, не зависит от пути перехода (определяется лишь начальным и конечным состояниями системы) - для квазистатических процессов неравенство Клаузиуса обращается в равенство  40.Закон рівномірного розподілу енергії за ступенями вільності. Число ступенів свободи: механічної системи називається кількість незалежних величин, з допомогою яких може бути задане положення системи. Одноатомний газ має три поступальні ступені свободи і = 3, тому що для опису положення такого газу в просторі досить трьох координат (х, y, z). Твердим зв'язком називається зв'язок, при якому відстань між атомами не змінюється. Двохатомні молекули із твердим зв'язком (N2, O2, Н2) мають 3 поступальні ступені свободи й 2 обертальні ступені свободи: i = iпост +iобер=3 + 2=5. Поступальні ступені свободи пов'язані з рухом молекули як цілого в просторі, обертальні - з поворотом молекули як цілого. Обертання відносного осей координат x і z на кут приведе до зміни положення молекул у просторі, при обертанні щодо осі y молекула не змінює своє положення, отже, координата φy у цьому випадку не потрібна. Трьохатомна молекула із твердим зв'язком має 6 ступені свободи i = iпост +iобер=3 + 3=6 Якщо зв'язок між атомами не твердий, то додаються коливальні ступені свободи. Для нелінійної молекули ікол. = 3N - 6, де N - число атомів у молекулі. Незалежно від загального числа ступенів свободи молекул 3 ступеня свободи завжди поступальні. Жодна з поступальних ступенів не має переваги перед іншими, тому на кожну з них доводиться в середньому однакова енергія, рівна 1/3 значення Больцман установив закон, згідно з яким для статистичної системи ( тобто для системи в якої число молекул велике), що перебуває в стані термодинамічної рівноваги на кожний поступальний і обертальний ступінь свободи доводиться в середньому кінетична енергія, рівна 1/2 kТ, і на кожний коливальний ступінь свободи - у середньому енергія, рівна kТ. Коливальний ступінь свободи « має» удвічі більшу енергію тому, що на неї доводиться не тільки кінетична енергія (як у випадку поступального й обертового руху), але й потенційна енергія, причому у такий спосіб середня енергія молекули 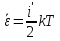 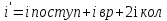 Ми будемо розглядати молекули із твердим зв'язком, тому  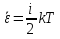 тому що в ідеальному газі взаємна потенційна енергія молекул дорівнює нулю (молекули не взаємодіють між собою), то внутрішня енергія 1 моля дорівнює добутку середньої енергії однієї молекули на число молекул у молі речовини, тобто на число Авогадро Для 41. Внутрішня енергія та теплоємність ідеального газу. Для ідеального газу внутрішня енергія залежить лише від температури, і калоричне рівняння набуває вигляду 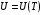 . .Цей експериментальний факт має назву закону Джоуля. Вигляд функції 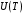 не може бути визначений методами термодинаміки, вона може бути лише виражена через теплоємність. Оскільки внутрішня енергія ідеального газу не залежить від об’єму не може бути визначений методами термодинаміки, вона може бути лише виражена через теплоємність. Оскільки внутрішня енергія ідеального газу не залежить від об’єму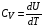 ; ;  . .Тоді повна внутрішня енергія дорівнює інтегралу 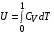 від початкового до кінцевого стану. Якщо сумістити початковий стан з нулем температури, то 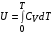 . .Але знову ж таки, розв’язати таке рівняння неможливо, оскільки теплоємність є невідомою функцією стану. Хоча для великої кількості газів у досить великих межах зміни  теплоємність є сталою величиною : теплоємність є сталою величиною :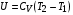 . . 42. Ентропія Поняття ентропії було вперше введено у 1865 році Рудольфом Клаузіусом. Він визначив зміну ентропії термодинамічної системи при оборотному процесі як відношення загальної кількості теплоти ΔQ, отриманої або втраченої системою, до величини абсолютної температури T: Рудольф Клаузіус дав величині S назву «ентропія», утворивши її від грецького слова τρoπή, «зміна» (зміна, перетворення). Формула визначає тільки зміну ентропії, а не її абсолютну величину, тому в термодинаміці ентропія визначається лише з точністю до сталої. Зв'язок між теплоємністю та ентропією дається формулою 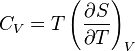 У 1877 році Людвіг Больцман зрозумів зв'язок між ентропією системи та кількістю можливих «мікростанів» (мікроскопічних станів), якими може реалізуватися макроскопічний стан із заданими властивостями. Розглянемо, наприклад, ідеальний газ у посудині. Мікростан визначений як положення та імпульси кожного атома, з яких складається система. Братимемо до уваги тільки ті мікростани, для яких: (i) розташування всіх частинок не виходить за межі посудини, (ii) загальна енергія газу, що визначається як сума кінетичних енергій атомів, дорівнює певній величині. Больцман постулював що де константа kB=1,38·10-23 Дж/К відома тепер як стала Больцмана, а є числом мікроскопічних станів, можливих у заданому макроскопічному стані. Цей постулат, відомий як принцип Больцмана, може розцінюватися, як початок статистичної механіки, яка описує термодинамічні системи використовуючи статистичну поведінку компонентів, із яких вони складаються. Принцип Больцмана зв'язує мікроскопічні властивості системи (Ω) з однією з її термодинамічних властивостей (S). Згідно з визначенням Больцмана, ентропія є функцією стану. Більш того, оскільки (Ω) може бути тільки натуральним числом (1,2,3...), ентропія повинна бути додатньою — виходячи з властивостей логарифма. У випадку дискретних станів квантової механіки підрахунок кількості станів не викликає проблем і проводиться звичайним чином. Складніше підрахувати кількість станів у рамках класичної механіки, в рамках якої мікроскопічний стан системи описується координатами й імпульсами окремих частинок, що пробігають неперервні значення. Для підрахунку станів у класичних системах фазовий простір розбивають на невеликі комірки із об'ємом, який відповідає зведеній сталій Планка. В такому випадку де — число незалежних координат, — зведена стала Планка, а інтегрування проводиться по об'єму фазового простору, який відповідає певному макроскопічному стану. Ентропія є екстенсивною величиною (залежить від маси і об'єму системи), тому сумарна ентропія двох систем Ентропія є функцією стану системи, її зміна не залежить від способу переходу з кінцевого стану у початковий: якщо обидва стани рівноважні. У самочинних процесах, які протікають в ізольованій системі, ентропія зростає (ΔS>0). Ця властивість є основою другого закону термодинаміки. Виходячи з означення ентропії за Больцманом, у самочинних процесах в ізольованій системі безладдя завжди зростає. Загалом, для довільної, не обов'язково ізольованої термодинамічної системи: де рівність виконується, за означенням, для рівноважних оборотних процесів. Ентропія залишається сталою при рівноважних оборотних процесах в ізольованій системі, тобто системі, що не обмінюється ні енергією, ні частинками з іншими системами. У неізольованих термодинамічних системах зміна ентропії підпорядкована першому закону термодинаміки. Процеси, що відбуваються зі сталою ентропією називаються ізоентропійними. Серед рівноважних процесів до таких належить адіабатичний процес. Ізоентропійними також можуть бути деякі нерівноважні процеси. Ентропію можна визнатити як похідну від термодинамічних потенціалів: від вільної енергії ГельмгольцаF 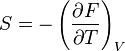 від вільної енергії ГіббсаG 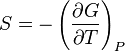 . .43.Статичні розподіли . Розподіли Больцмана. Розподіл Больцмана можна розглядати, як узагальнення барометричного розподілу на випадок довільного потенціального поля  (іще кажуть, довільного потенціалу). Справді, не має підстав вважати, що поведінка газу суттєво зміниться, якщо замість сил тяжіння будуть діяти інші сили. (іще кажуть, довільного потенціалу). Справді, не має підстав вважати, що поведінка газу суттєво зміниться, якщо замість сил тяжіння будуть діяти інші сили. Відповідно, за барометричною формулою 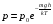 , (1) , (1)де 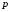 - тиск на висоті - тиск на висоті  , ,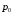 - тиск біля поверхні Землі - тиск біля поверхні Землі 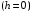 . .Враховуючи, що для ідеального разу 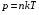 , (2) , (2)формула (1) набуває вигляду 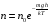 . (3) . (3)Як розуміти цю формулу. 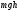 - потенціальна енергія молекули на висоті - потенціальна енергія молекули на висоті 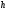 в однорідному гравітаційному полі. Тому, якщо газ знаходиться в реальному силовому полі, і його частинки мають певну потенціальну енергію, то кількість часток з потенціальною енергією в однорідному гравітаційному полі. Тому, якщо газ знаходиться в реальному силовому полі, і його частинки мають певну потенціальну енергію, то кількість часток з потенціальною енергією 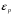 визначаються формулою Больцмана визначаються формулою Больцмана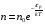 . (4) . (4)Відповідно 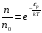 - (5) - (5)доля частинок, що в умовах теплової рівноваги мають потенціальну енергію 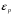 . .Приклад. Оскільки енергія магнітної частинки з магнітним моментом 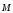 дорівнює дорівнює  , то таких частинок в деякому об’ємі , то таких частинок в деякому об’ємі 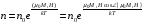
Поведінка ідеального газу в певному об’ємі не залежить від наявності інших газів. В стані термодинамічної рівноваги концентрація різних газів в суміші повинні убувати з висотою за різними експонентами, що визначаються молекулярною вагою відповідних компонент (концентрація легких компонент убувають повільніше). В реальній тропосфері не спостерігаються зростання концентрації легких газів із висотою, внаслідок процесів, що призводять до перемішування її нижніх і верхніх шарів. 44.Закон розподілу Максвела. Розподіл Максвела по швидкостях Внаслідок багаторазових зіткнень молекул газу між собою та зі стінками посудини, в якій міститься велика кількість молекул, встановлюється деякий статистичний розподіл молекул за швидкостями. Дж. Максвелл у 1859 році вивів закон розподілу молекул за швидкостями, використавши основні положення молекулярно-кінетичної теорії: 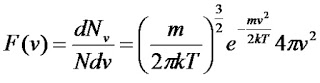 Як видно з наведеної формули, функція розподілу Максвелла залежить від температури газу, маси частинок і їхньої швидкості.
На малюнку представлені типові криві розподілу молекул за швидкостями. По осі абсцисс відкладено модуль швидкості, а по осі ординат – відносне число молекул, швидкості яких лежать в інтервалі від υ до υ + Δυ. Це число дорівнює площі виділеного на стовпця. З графіку розподілу молекул за швидкостями можемо зробити наступні висновки. 1. Крива розподілу проходить через початок координат, що свідчить про те, що немає молекул, які б не рухались. 2. Крива має максимум, після якого асмптотично наближається до осі абсцис. Отже дуже великі швидкості малоймовірні. Вони можливі тільки за умови, що молекула при багатьох зіткненнях з іншими молекулами діставатиме енергію, а не віддаватиме її, що є можливим, але дуже малоймовірним. |

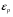 . Тобто для молекул з великою енергією завжди мала.
. Тобто для молекул з великою енергією завжди мала.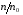 спадає із зростанням
спадає із зростанням