1. Предмет і метод фізики та її зв'язок з суміжними науками
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
Перетворення[ред. • ред. код]Перетворення Галілея дозволяють описати фізичне явище в інерційній системі відліку якщо відомо як виглядає дане фізичне явище в іншій інерційній системі відліку. Якщо осі координат у двох системах відліку мають одинакові напрямки, а одна система рухається вздовж осі другої системи з постійною швидкістю , то перетворення мають вигляд: Відповідно змінюються компоненти швидкості Інші величини, такі як прискорення, сила, маса при перетвореннях Галілея не змінюються. Відповідно, не змінюється вигляд рівнянь Ньютона. Говорять, що рівняння Ньютона інваріантні відносно перетворень Галілея. 5.Сила маса імпульс. Закони Ньютона. .Си́ла — фізична величина, що характеризує ступінь взаємодії тіл. Якщо на дане тіло діють інші тіла, то ця дія (взаємодія) проявляється у зміні форми і розмірів тіла (тіло деформується), або/та у зміні швидкості тіла (тіло рухається зприскоренням)[1]. У першому випадку маємо статичний прояв сили, у другому — динамічний. Виходячи з цього можливі два способи визначення сили: за деформацією тіла (наприклад, пружини) і за прискоренням, отриманим тілом. Сила є векторною величиною — крім числа, що позначає більшу чи меншу дію, вона характеризується ще й точкою прикладання та напрямком дії. Силу здебільшого позначають латинською літерою (від англ. force), де жирний шрифт вказує, що це вектор. Вектор також позначають стрілочкою . Абсолютна величина сили позначається нежирним шрифтом: . Сили вивчаються в розділах механіки, які називаються динамікою і статикою. Динаміка вивчає питання, пов'язані з рухомтіл під впливом сил, а в статиці розглядаються умови рівноваги нерухомих тіл. Маса — фізична величина, яка є однією з основних характеристик матерії, що визначає її інерційні, енергетичні та гравітаційнівластивості. Маса зазвичай позначається латинською літерою m. Імпульсом або вектором кількості руху в класичній механіці називається міра механічного руху тіла, векторна величина, що для матеріальної точки дорівнює добутку маси точки на її швидкість та має напрямок швидкості. У системі СІ одиницею вимірювання імпульсу є кг·м/с, в системі СГС — [г·см/с]. Сума імпульсу для будь-якої замкнутої системи є величиною сталою. Перший закон НьютонаПерший закон Ньютона стверджує, що існують системи відліку, у яких тіла зберігають стан спокою або рівномірного прямолінійного руху за відсутності дії на них з боку інших тіл або при взаємній компенсації цих впливів.[4] Такі системи відліку називаються інерційними. Ньютон припустив, що кожен масивний об'єкт має певний запасінерції, який характеризує «природний стан» руху цього об'єкта. Ця ідея заперечує погляд Аристотеля, який розглядав спокій «природним станом» об'єкта. Перший закон Ньютона суперечить фізиці Аристотеля, одним з положень якої є твердження про те, що тіло може рухатися з постійною швидкістю лише під дією сили. Той факт, що в механіці Ньютона в інерційних системах відліку спокій фізично не відрізняється від рівномірного прямолінійного руху, є обґрунтуванням принципу відносності Галілея. Серед сукупності тіл принципово неможливо визначити які з них перебувають «у русі», а які «знаходяться у спокої». Говорити про рух можна лише відносно якоїсь системи відліку. Закони механіки виконуються однаково у всіх інерційних системах відліку, іншими словами всі вони є механічно еквівалентними. Останнє випливає з так званих перетворень Галілея.[7] Другий закон НьютонаДругий закон Ньютона у сучасному формулюванні записується так: в інерційній системі відліку швидкість зміни імпульсу матеріальної точки дорівнює векторній сумі усіх сил, що діють на цю точку. де − імпульс матеріальної точки, − сумарна сила, що діє на матеріальну точку. Другий закон Ньютона стверджує, що дія незбалансованих сил приводить до зміни імпульсу матеріальної точки[4]. З означення імпульсу: 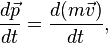 де − маса, − швидкість. У класичній механіці при швидкостях руху, що значно менші за швидкість світла маса матеріальної точки вважається сталою, що дозволяє виносити її за цих умов за знак диференціала: З врахуванням визначення прискорення точки, другий закон Ньютона набуде вигляду: Вважається, що це друге найпоширеніше формулювання у фізиці, хоча сам Ньютон ніколи явним чином записував цей закон у такому вигляді. Вперше дане формулювання можна зустріти у працях К. Маклорена та Л. Ейлера. Оскільки в будь-якій інерційній системі відліку прискорення тіла є однаковим і не змінюється при переході від однієї системи до іншої, то й сила є інваріантною по відношенню до такого переходу. У всіх явищах природи сила, незалежно від свого походження, проявляється тільки в механічному сенсі, тобто як причина порушення рівномірного і прямолінійного руху тіла в інерційній системі координат. Зворотне твердження, тобто встановлення факту рівномірного прямолінійного руху, не свідчить про відсутність сил, що діють на тіло, а лише про те, що дії цих сил взаємно врівноважуються. Іншими словами: їх векторна сума є вектор з модулем, рівним нулю. На цьому ґрунтується вимірювання величини сили, коли вона компенсується силою, величина якої відома. Другий закон Ньютона дозволяє обчислювати величину сили. Наприклад, знання маси планети Сонячної системи і її доцентрового прискорення при русі по орбіті дозволяє обчислити величину сили гравітаційного тяжіння, що діє на цю планету з боку Сонця. Третій закон НьютонаДля двох довільних тіл (наприклад, тіло 1 і тіло 2) третій закон Ньютона стверджує, що сила дії тіла 1 на тіло 2 супроводжується появою рівної за модулем, але протилежно спрямованої сили, що діє на тіло 1 з боку тіла 2.[8]. Математично закон записується так: Цей закон вказує, що сили завжди виникають парами «дія-протидія».[4] Якщо тіло 1 і тіло 2 знаходяться в одній системі, то сумарна сила в системі, обуиовленявзаємодією цих тіл дорівнює нулю: Це означає, що в замкнутій системі не існує незбалансованих внутрішніх сил. Це приводить до того, що центр мас замкнутої системи не може рухатись з прискоренням. Окремі частини системи можуть прискорюватися, але лише таким чином, що система у цілому залишиться у стані спокою або рівномірного прямолінійного руху. Однак у випадку, якщо зовнішні сили почнуть діяти на систему, то її центр мас почне рухатись з прискоренням, що пропорційне зовнішній результуючій силі і обернено пропорційним до маси системи 6.Центр мас систем. Закон руху центра Система центру мас — інерційна система відліку, початок якої розташований у центрі інерції механічної системи. Це́нтр іне́рції або центр мас системи матеріальних точок масою із радіус-векторами визначається як У випадку суцільного тіла із густиною 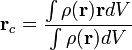 Зручність введення поняття центру інерції в тому, що рівняння руху для нього в багатьох випадках можна відокремити від рівнянь руху складових системи матеріальних точок відносно цього центру. Наприклад, центр руху замкненої системи матеріальних часток рухається у інерційній системі координат рівномірно й прямолінійно. В такому випадку зручно перейти до системи центру мас, тобто зв'язати початок системи координат з центром інерції і розглядати лише відносний рух часток, які входять в систему. Схожа ситуація виникає тоді, коли система незамкнена, але сили, які діють на матеріальні точки пропорційні їхнім масам. Таку властивість мають сили тяжінння. В такому випадку центр інерції рухається з прискоренням, яке визначається відношенням сумарної сили до повної маси системи часток. Систему матеріальних часток можна розглядати, як одну матеріальну частку із масою, яка дорівнює сумарній масі усіх часток, розташовану в центрі інерції. Рух твердого тіла довільної форми можна розділити на поступальний рух центру мас та обертальний рух відносно цього центру. Закон руху центра мас У системі матеріальних точок існує точка, яка при відсутності дії зовнішніх сил рухається по прямій лінії. Цю точку називають центром мас, або центром інерції. Центром мас системи матеріальних точокназивають точку, в якій зібралася б уся маса системи матеріальних точок при взаємодії їх з силами притягання, що нескінченно зростають. Радіус-вектор центра мас для тіл з дискретним розподілом мас визначається за формулою: 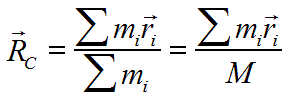 де 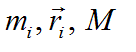 – відповідно маси, радіуси-вектори матеріальних точок і маса всієї системи. – відповідно маси, радіуси-вектори матеріальних точок і маса всієї системи.7. Неінерціальні системи відліку. Сили інерції. Закони Ньютона, як відомо, справедливі лише в тих системах відліку, які рухаються одні відносно одних прямолінійно і рівномірно. Такі системи відліку називаються інерціальними системами відліку. В таких системах відліку основним рівнянням руху матеріальної точки є рівняння, яке виражає другий закон Ньютона: На практиці часто доводиться мати справу з системами відліку, які рухаються відносно інерціальних систем відліку з прискоренням. Такі системи відліку називаються неінерціальними. Матеріальна точка внеінерціальній системі відліку може рухатися прискорено під дією сил, виникнення яких не можна пояснити дією якихось окремих тіл. Ці сили називаються силами інерції. Перший закон Ньютона в неінерціальних системах немає сенсу. Оскільки в неінерціальних системах відліку крім сил взаємодії існують ще і сили інерції, то третій закон Ньютона настільки спотворюється, що і він втрачає чіткий фізичний зміст. Для сил інерції протидії не існує. Сили інерції зумовлені властивістю тіл зберігати стан спокою або рівномірного прямолінійного руху. Другий закон Ньютона в неінерціальних системах має вигляд: де – прискорення тіла, визначене в неінерціальній системі відліку, – сили інерції. Си́ла іне́рції — фіктивна сила, яку вводять для опису динаміки механічного руху в неінерційних системах відліку. , де — сила інерції, m — маса, — прискорення, з яким рухається система координат. На погляд спостерігача, який рухається з прискоренням, навколишні фізичні тіла здійснюють рухи, які не відповідають тим силам, що на них діють. Так, наприклад, коли потяг рушає з місця, спостерігачу, який сидить у вагоні, здається, що вокзал рушив у протилежний бік, хоча на нього не діють жодні сили. Для того, щоб мати змогу застосовувати Ньютонівську механіку в неінерційній системі координат, вводяться фіктивні сили інерції, що діють у цій системі на всі тіла. Так, на погляд спостерігача у вагоні потягу, другий закон Ньютона виконується, якщо на вокзал діє сила -ma, де m — маса вокзалу, a — прискорення руху спостерігача. 8. Механическая работа і потужність 8. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы[1] Визначається механічна робота формулою: A = Fs, де A — робота, F — сила, s — пройдений шлях. Потужність (N, P, W) — робота, що виконана за одиницю часу, або енергія, передана за одиницю часу: де N — потужність, А — виконана робота, t — проміжок часу, за який ця робота виконана. В СІ питома теплота пароутворення вимірюється у Ватах. Іншою одиницею вимірювання, яка ще й досі широко використовується, є кінська сила (1 к.с. = 735,5 Вт). Потужність є важливою характеристикою двигунів. 9.Кінети́чна ене́ргіята потенціальна енергія Кінети́чна ене́ргія — частина енергії фізичної системи, яку вона має завдяки руху. Кінетичну енергію заведено позначати або .У випадку частинки із масою та швидкістю кінетична енергія дається формулою Потенціа́льна ене́ргія — частина енергії фізичної системи, що виникає завдяки взаємодії між тілами, які складають систему, та із зовнішніми щодо цієї системи тілами, й зумовлена розташуванням тіл у просторі. Разом із кінетичною енергією, яка враховує не тільки положення тіл у просторі, а й рух, потенціальна енергія складає механічну енергію фізичної системи. Потенціальна енергія матеріальної точки визначається як робота з її переміщення із точки простору, для якої визначається потенціальна енергія у якусь задану точку, потенціальна енергія якої приймається за нуль. Потенціальна енергія визначається лише для поля консервативних сил. Потенціальна енергія здебільшого позначається літерами або . 10.Зіткнення двох тіл   11.Момент сили ,момент імпульсу. Основний закон динаміки обертального руху. Моментом сили відносно нерухомого центра О називається векторна величина , що дорівнює векторному добутку радіуса вектора  , проведеного з точки О до точки прикладання сили, на вектор сили , проведеного з точки О до точки прикладання сили, на вектор сили 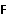 . .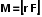 . (1.11) . (1.11)Вектор 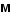 напрямлений перпендикулярно до площини, у якій лежать вектори напрямлений перпендикулярно до площини, у якій лежать вектори 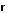 і і 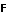 , таким чином, що з його кінця найкоротший поворот від вектора , таким чином, що з його кінця найкоротший поворот від вектора 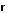 до вектора до вектора 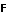 видно проти напряму руху годинникової стрілки. видно проти напряму руху годинникової стрілки.Моментом імпульсуматеріальної точки відносно нерухомої точкиназивається векторний добуток радіус-вектораматеріальної точки, який проведений з точки, на імпульс цієї матеріальної точки(рис. 15): ![[image]](22815_html_711a8b56.png) Модуль вектора моменту імпульсу Векторна сума моментів імпульсу всіх матеріальних точок тіла називається моментомімпульсу тіла відносно точки : ![[image]](22815_html_m7874ee07.png) . .Моментом імпульсу тіла відносно нерухомої осіназивається скалярна величина, яка дорівнює проекції на цю вісь вектора моменту імпульсу тіла відносно довільної точкина осі OZ. Значення моменту імпульсу не залежить від положення точки на осі OZ. Знайдемо вираз для моменту імпульсу тіла відносно осі обертання. Проекція результуючого вектора на деяку вісь дорівнює алгебраїчній сумі проекцій на цю вісь усіх складових векторів: ![[image]](22815_html_65f632bd.png)   13. Момент інерції   14. Теорема Штейнера момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела IС относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями . 15. Кінетична енергія тіла що обертається навколо не рухомої осі Кінетична енергія тіла, що рухається довільно, дорівнює сумі кінетичних енергій всіх матеріальних точок, на які це тіло можна умовно поділити: ![[image]](22815_html_m3b932655.png) . .Якщо тіло обертається навколо нерухомої осі з кутовою швидкістю , то , де – відстань від цієї точки до осі обертання. Отже, ![[image]](22815_html_m5c4a14e8.png) . .Якщо тверде тіло рухається поступально з швидкістю і одночасно обертається з кутовою швидкістю навколо осі, що проходить через його центр інерції, то його кінетична енергія ![[image]](22815_html_m3293a53c.png) . .16.Закон всесвітнього тяжіння. Космічні швидкості. 16. Гравітаційні сили – це сили притягання, які діють між усіма тілами. Величина гравітаційної взаємодії для двох точкових тіл визначається законом всесвітнього тяжіння: Між будь-якими двома тілами діє сила взаємного притягання, прямо пропорційна добутку їхніх мас і обернено пропорційна квадрату відстані між ними: Особливістю цих сил є те, що для тіл з малими масами вони проявляються дуже слабо, а для масивних тіл є дуже великими. 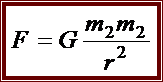  перша, друга, третя – критичні значення швидкості літального аппарта в момент його виходу на орбіту, що визначають форму траєкторії його руху в космічному просторі. К. с. можуть бути обчислені для будь-якої відстані r від центра Землі, однак найбільше часто К. с. визначаються тільки для поверхні кульової однорідної моделі Землі (радіусом 6371 км). Перша К. с. – мінімальна швидкість, при якій космічний апарат у гравітаційному полі Землі може стати штучним супутником Землі. Обчислюється по формулі v1=(GM/r)1/2, де GМ =398603 км3/з2 (G – постійна тяжіння, М – маса Землі). Перша К. с. називається також коловою швидкістю; якщо в момент виходу на орбіту літальний апарат має швидкість, перпендикулярну напрямку на центр Землі й рівну v, те його орбіта (при відсутності збурювань) буде круговою. У поверхні Землі перша К. с. має значення v = 7,91 км/с. Друга К. с. – мінімальна швидкість, необхідна для того, щоб літальний апарат перетворився в штучного супутника Сонця. Застосовуються також й інші назви: швидкість втікання, швидкість ускользания, а також параболічна швидкість, тому що літальний апарат з початковою швидкістю vII рухається по параболічній траєкторії, віддаляючись як завгодно далеко від Землі, залишаючись при цьому в межах Сонячної системи. Швидкості менше параболічної називаються еліптичними, більше – гіперболічними. Друга К. с. визначається по формулі vII = (2GM/r)l/2; у поверхні Землі vII = 11186 км/с. Третя К. с. – мінімальна швидкість, необхідна для того, щоб літальний апарат, запущений у Землі, переборов притягання Сонця й покинув Сонячну систему. Третя К. с. визначається з умови, що літальний апарат повинен мати параболічну швидкість щодо Сонця, поблизу орбіти Землі ця швидкість дорівнює близько 42 км/с. Щоб її досягти, тіло в поверхні Землі повинне придбати швидкість vIII = 16,67 км/с. Поняття К. с. застосовуються також при аналізі руху літального апарата в гравітаційних полях інших планет або їхніх супутників, Сонця. 17. Спецальна теорія відносності. Постулати ейнштейна Перетворення Лореца. Взаємозвязок маси та імпульсу. Маси та енергії 17. Постулати Ейнштейна Теорія відносності описує рух тіл із швидкостями, близькими до швидкості світла. При малих швидкостях закони теорії відносності співпадають із законами класичної механіки. Таким чином, застосування законів класичної механіки обмежено. Вони застосовуються тільки для опису руху макротіл із швидкостями в багато разів меншими швидкості світла. Спеціальна теорія відносності Ейнштейна будується на 2 постулатах: 1. Принцип відносності:ніякі досліди (механічні, електричні, оптичні), які проведені всередені даної інерціальної системи відліку, не дають можливості виявити, чи знаходиться ця система в стані спокою чи рухається рівномірно і прямолінійно: всі закони природи інваріантні відносно переходу від однієї інерціальної системи відліку до іншої. 2. Принцип інваріантності швидкості світла. Швидкість світла у вакуумі не залежить від швидкості руху джерела або спостерігача і однакова у всіх інерціальних системах відліку. Ейнштейн показав, що у відповідності з постулатами теорії відносності зв’язок між координатами і часом в двох інерціальних системах відліку К і К¢ (нерухомій і рухомій) здійснюється не перетвореннями Галілея, а перетвореннями Лоренца: 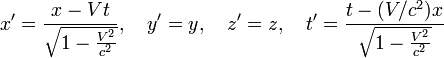 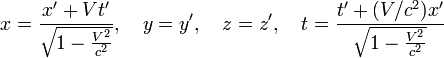 Перетворення Лоренца переходять у перетворення Галілея якщои«с . ВЗАЄМОЗВ'ЯЗОК МАСИ ТА ЕНЕРГІЇ За законами Ньютона, якщо на тіло діє сила, то воно рухається з прискоренням. Якщо напрямок дії сили збігається з напрямком руху, то швидкість тіла має необмежено зростати. Проте це твердження суперечить принципу СТВ, згідно з яким існує гранична швидкість передачі взаємодії— швидкість світла. Як з'ясував А. Ейнштейн, щоб закони Ньютона були інваріантними в усіх інерціальних системах відліку і відповідали положенням СТВ, слід переглянути деякі класичні уявлення про рух і взаємодію тіл. Зокрема, за допомогою математичних перетворень формули другого закону Ньютона він встановив, що маса тіла залежить від швидкості його руху: 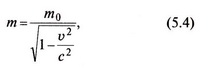 де m — маса тіла, що рухається зі швидкістю v; mo — маса тіла, яке перебуває в стані спокою; с — швидкість світла. Згідно з другим принципом СТВ, не існує систем відліку, в яких би швидкість руху тіла перевищувала швидкість поширення світла у вакуумі Масу т називають релятивістською масою, що залежить від швидкості; т0— масою спокою. Обидві величини характеризують інертні властивості тіла у різних станах: під час руху тіла або у спокої Цей висновок усував існуюче протиріччя між класичною механікою і теорією відносності, оскільки за цих умов рівняння руху ставали інваріантними для всіх інерціальних систем відліку: 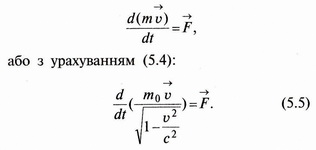 Рівняння руху релятивістської і класичної механіки мають однакову форму незалежно від швидкості руху тіла Якщо швидкість тіла незначна (v << с), то залежністю маси тіла від швидкості можна знехтувати, адже підкореневий вираз у знаменнику формули (5.5) наближається до l, а m = m0. Отже, рівняння руху (5.5) у релятивістській і класичній фізиці має однаковий вигляд. В узагальненій формі його можна записати як 18. Механічні коливання.Гармонічні коливання 18. Коливаннями або коливальними рухами називають такі види механічного руху чи зміни стану системи, які періодично повторюються в часі, наприклад, механічні коливання тіла на пружині, коливання маятників, коливання струн, вібрації фундаментів будівель, електромагнітні коливання в коливальному контурі. За фізичною природою коливання поділяють на механічні та електромагнітні, за характером коливань - на вільні, вимушені та автоколивання. Хоча коливання досить різноманітні за своєю фізичною природою, але вони мають спільні закономірності й описуються однотипними математичними методами. Механічні коливання - періодичне зміщення тіла то в один, то в другий бік відносно положення рівноваги. Механічна система, в якій одне або декілька тіл можуть здійснювати коливальні рухи, називають коливальною системою. Коливання називають періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим прикладом періодичних коливань є гармонічні коливання, під час яких фізична величина змінюється з плином часу за законом x = Asin(wt + j0), або x = Acos(wt + j0), (5.1.1) де А, w, і j0 - постійні величини, причому А > 0, w > 0. 19.Вільні не затухаючі коливання 19. Коливання, які відбуваються лише під дією внутрішніх сил, називають вільними. Щоб система виконувала ці коливання, треба вивести тіло з положення рівноваги, тобто надати коливальній системі енергію. При цьому рівнодійна всіх сил, що діють на тіло, має бути відмінною від нуля і спрямованою до положення рівноваги, в якому рівнодійна дорівнює нулю. Вільні коливання виникали б, якби не було впливу зовнішніх сил. Цього досягти неможливо, тому вільні коливання це абстракція. Вони з часом стають згасальними. Виникла потреба в коливаннях під дією зовнішньої сили, що періодично змінюється, такі коливання називають вимушеними. Ці коливання здійснюють поршні в циліндрах двигунів, голка швацької машини тощо. Ще одним видом незагасальних коливань є автоколивання. Це коливання, які підтримуються внутрішніми джерелами енергії системи, коли не діє зовнішня періодична сила. Наприклад, настінний годинник з маятником або наручний механічний годинник - це механічні автоколивальні системи. У годинниках потенціальна енергія тягарця (або стиснутої пружини) поступово, окремими порціями передається маятнику і компенсує втрати на тертя. Можна спостерігати автоколивання струни під дією смичка, голосових зв'язок під час розмови або співу. 20.Енергія системи, яка виконує гармонічні коливання. 20. Кінетична енергія матеріальної точки, яка здійснює прямолінійні гармонічні коливання, дорівнює 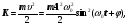 (11) (11)або К = 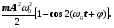 (12) (12)Потенціальна енергія матеріальної точки, яка здійснює гармонічні коливання під дією пружної сили F, дорівнює П = - 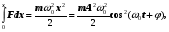 (13) (13)або П = 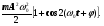 (14) (14)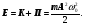 К і Π змінюються в часі з частотою, яка у два рази перевищує частоту гармонічного коливання. Оскільки середні значення 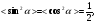 то то 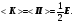 21.Векторне зображення гармонічних коливань 22. Складення направлення одного направлення 22. Складання кількох гармонійних коливань одного напрямку і однакової частоти стає наочним, якщо зображати коливання графічно у виглядівекторів на площині. Отримана таким способом схема називається векторною діаграмою. Візьмемо вісь, уздовж якої будемо відкладати коливну величину x. З взятої на осі точки О відкладемо вектор довжини A, утворює з віссю кут б. Якщо привести цей вектор в обертання з кутовою швидкістю щ0, то проекція кінця вектора буде переміщатися по осі x в межах від-А до + A, причому з координат проекції буде змінюватися з часом за законом 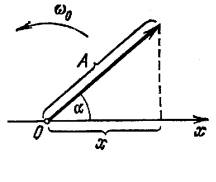 Отже, проекція кінця вектора на вісь буде здійснювати гармонічні коливання з амплітудою, що дорівнює довжині вектора, з круговою частотою, рівною кутовий швидкості обертання вектора, і з початковою фазою, що дорівнює куту, утвореному вектором з віссю в початковий момент часу. 23.Складення взаємно перпендикулярних коливань Уявімо дві взаємно перпендикулярні векторні величини x і y, що змінюються з часом з однаковою частотою щ за гармонійним законом, то (1) Де ex і eу - орти координатних осей x і y, А і B - амплітуди коливань. Величинами x і у може бути, наприклад, зміщення матеріальної точки (частки) з положення рівноваги. У разі частки, що коливається величини , (2) визначають координати частинки на площині xy. Частка буде рухатися по деякій траєкторії, вигляд якої залежить від різниці фаз обох коливань. Вирази (2) представляють собою задане в параметричній формі рівняння цієї траєкторії. Щоб отримати рівняння траєкторії в звичайному вигляді, треба виключити з рівнянь (2) параметр t. З першого рівняння випливає, що (3) Відповідно (4) Розгорнемо косинус в другому з рівнянь (2) за формулою для косинуса суми: Підставимо замість cos щt і sinщt їх значення (3) і (4): Перетворимо це рівняння Це рівняння еліпса, осі якого повернені щодо координатних осей х і у. Орієнтація еліпса і його півосі залежать досить складним чином від амплітуд A і В і різниці фаз б. 23.характеристики затухаючих коливань . Розглянемо вільні затухаючі коливання – коливання, амплітуда яких внаслідок втрати енергії реальною коливальною системою з плином часу зменшується. Простим механізмом зменшення енергії коливань з’являється її перетворення в теплоту внаслідок тертя в механічних коливальних системах, а також омічних втрат і випромінювання електромагнітної енергії в електричних коливальних системах. Закон затухаючих коливань визначається властивостями коливальних систем. Звичайно розглядають лінійні системи – ідеалізовані реальні системи. Лінійними системами являються, наприклад, пружинні маятники при малому розтягуванні пружини (коли слушний закон Гука), коливальний контур, індуктивність, ємність і опір якого не залежить ні від струму в контурі, ні від напруги. Різні по своїй природі лінійні системи описуються ідентичними лінійними диференціальними рівняннями, що дозволяє підходити до вивчення коливань різної фізичної природи з єдиної точки зору, а також проводити їх моделювання, в тому числі і на ЕВМ. Диференціальне рівняння вільних затухаючих коливань лінійної системи задається у вигляді: де S – коливальна величина, що описує той чи інший фізичний процес, d - const - коефіцієнт затухання, - циклічна частота вільних незатухаючих коливань тієї ж коливальної системи, тобто при d = 0 (при відсутності втрат енергії). Рішення рівняння у випадку малих згасань ( де 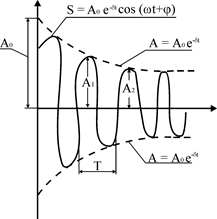 Рис. Проміжок часу , за який час амплітуда затухаючих коливань зменшується в е разів, зветься часом релаксації. Якщо затухання мале, то можна умовно користуватись поняттям періоду як проміжок часу між двома послідовними максимумами (чи мінімумами) коливальної фізичної величини. Тоді період затухаючих коливань з урахуванням формули 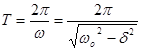 . .Якщо A(t) і A(t+T) - амплітуди двох послідовних коливань, відповідних моментам часу, що відрізняються на період, то відношення називається декрементом затухання, а його логарифм N – число коливань, здійснюваних за час зменшення амплітуди у е разів. Для характеристики коливальної системи користуються поняттям добротності Q яка при малих значенням логарифмічного декремента дорівнює Застосуємо висновки, одержані для вільних затухаючих коливань лінійних систем, для коливань різної фізичної природи, для пружинного маятника масою m , що здійснює малі коливання під дією пружної сили F = -кх , сила тертя пропорційна швидкості, тобто За даних умов закон руху маятника матеме вигляд: Використовуючи формулу Маятник коливається по закону Диференціальне рівняння вільних затухаючих коливань заряду в контурі (при R ¹ 0) має вигляд: Коефіцієнт затухання На закінчення відмітимо, що при збільшенні коефіцієнта затухання період затухаючих коливань зростає і при обертається в безкінечність, тобто рух перестає бути періодичним. В даному випадку коливальна величина асимптотично наближається до нуля, коли t ®¥. Процес не буде коливальним. Він зветься аперіодичним. 25.Затухаючі коливання. Згасаючі коливання — коливання, енергія яких зменшується з плином часу. Процес, що триває нескінченно, виду Коливання можна описати такими типами:
26. Вимушені коливання. Вимушені коливання - коливання, які відбуваються під дією зовнішньої (будь-якої, яка змушує відбуватися коливання) сили. Вимушені коливання, коливання, що виникають в якій-небудь системі під дією змінної зовнішньої сили (наприклад, коливання мембрани телефону під дією змінного магнітного поля, коливання механічної конструкції під дією змінного навантаження і т.д.). Характер Ст до. визначається як характером зовнішньої сили, так і властивостями самої системи. На початку дії періодичної зовнішньої сили характер Ст до. змінюється з часом (у частковості, Ст до. не є періодичними), і лише після деякого часу в системі встановлюються періодичні Ст до. з періодом, рівним періоду зовнішньої сили (сталі Ст до.). Встановлення Ст до. у коливальній системі відбувається тим швидше, чим більше загасання коливань в цій системі. Вимушені коливання мають свою відмінну особливість – вони носять незатухаючий характер. Їх частота дорівнює частоті періодичного зовнішнього впливу на дану коливальну систему. Однак необхідно відрізняти такі коливальні рухи від автоколивань. При автоколиваннях в системі передбачається механізм, “поставляє” в систему з певного резервуара енергії, в такт з своїм коливанням, незначні порції енергії, що підтримують власні незгасаючі коливання. Таким чином, при автоколиваннями система «підштовхує» сама себе. При вимушених коливаннях система бере поштовх від сторонньої сили. 27. Резонанс. Резона́нс — явище сильного зростання амплітуди вимушеного коливання у разі, коли частота зовнішньої сили збігається з власною частотою коливань. Резонанс характеризують інтенсивністю, напівшириною спектральної лінії та добротністю. Здебільшого резонанс наближено описують кривою Лоренца де ω — частота зовнішньої сили, ω0 — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії. |
